列車制動衝突解析法

mail to: adrs
 BBS
BBS
戻る
前 		LIST
主目次 		Diary INDEX
日記list

　過走事故や衝突事故は、停止位置や走行状況から事故発生状況が計算でかなり明白になることが多い。現象を分解整理すれば加速減速運動と衝突だけだから、処理手順が明らかにされていれば、必要データを集めて中学・高校レベルの計算力で充分結論が得られる。その自ら得た結果から借り物ではない自分自身の判断をすることができ、関係者が誤信していたり必死に伏せているものも見えてくる。
　そういう観点から鉄道車両の、減速運動（加速運動）、衝突運動(完全弾性衝突／非弾性衝突)について以下に整理してみたい。「丸暗記すべき公式」ではなく、考え方を記述する方程式として読んで戴けると内容理解に直結します。本来「公式」は結果として形成されるものですから。（遠心力と重力の関係は別稿、曲線の速度制限を参照）

制動定数Ｋとは　<K>

　列車の制動距離Lがほぼ速度Vの２乗に比例することからその比例定数を「制動定数Ｋ」と呼ぶ。現場で使う比例定数なので換算係数が要らず概算には単純便利である。式で表せば
　　　V2＝K･L　　　　　速度2＝K･距離
　　　L＝V2／K　………(1)
である。この制動定数Ｋは、ATS-Sロング地上子(129.3kHz)の設置位置決定式に用いられて、非常制動を掛けた場合の最低基準値として、電車・気動車で20/0.7、旅客機関車列車で20、貨物列車で15と定められた。それが後日、通産省による国際単位SI強制により使用が禁じられて、教本には解説なしの定数として扱われている。
　95km/hの電車が非常制動を掛けた場合の停止までの制動距離Lは、制動定数Kが20/0.7だから、
　　L＝952／(20/0.7)＝315.875m、客車列車では L＝952／20＝451.25m
という形で活用する。
　なお、[m/s2]MKSA、[km/h/s]、α[K] の相互関係は、後述(10)-3の通り、
α[m/s2]MKSA＝3.6*α[km/h/s]＝7.2(3.6*α)[K]≡25.92*α[K]
α'[km/h/s]＝7.2*α'[K] 　……………………………（（単位換算は後述→(10)-3式参照））

　途中の速度V1への減速距離は、停止までの距離の差だから
　　L＝（V02−V12）／Ｋ　………(1)-2
　高速貨物列車（制動定数15）が 95km/h→45km/hに減速するのに必要な制動距離は、(1)-2式より、L＝（952−452）／15＝466.667m となる。

空走時間Tnと空走距離　<Tn>

　空走時間には、ブレーキ操作から効き始めるまでの時間の他、ATSでは受信解読時間と、システムに定められた余裕時間があり、その総計時間だけ空走してから制動される。
　空走距離は空走時間に速度を乗じれば算出できるが、単位系を統一することが必要だ。この場合秒単位だから、時速を秒速に換算する必要がある。
　　1 [km/h＝1000m/3600s＝(1/3.6)m/s]＝1/3.6 [m/s]、
　　1 [m/s＝(km/1000)/(h/3600)＝3.6 km/h]＝3.6 [km/h] ………(2)
という換算率だ。（組合せ単位の単位換算は上記下線部の様な演算で行えば換算率の勘違い記憶エラー発生を抑制できる。J、T、N、Hz、gal などの固有単位でも元の組合せ単位に戻せば同様の換算ができる。度分秒換算が絡んで60と3600の勘違いとか、PC上の三角比がrad:ラジアンで扱うべき処を電卓並に度分秒で扱ってしまうとかは注意深く扱う他はないが、）
　ATS-Sxでは、ATS受信時間1秒、確認扱い応答余裕時間5秒、ブレーキの応答時間が電車・気動車1秒、客車列車2秒、一般貨物列車5秒と定めている。

　従ってATS-Sロング警報で95km/hでの最大空走距離は、
電車の場合で 95k/3.6×(1+5+1)s=184.7m、（停止までは 184.7m＋315.9m＝500.6ｍ）
客車列車では 95k/3.6×(1+5+2)s=211.1m と算出される。（停止までは211.1m＋451.3m＝662.35ｍ）
(最大空走時間11秒の貨物列車は非常制動での停止距離600m制限もあって95km/h走行ができない)

等加速運動　<Acc>

　　 【常用加速度単位：km/h/s】　<Unit>

　電車の加速度は常用では毎秒時速：km/h/sで語られることが多いが、理論計算に当たっては直の計算には乗らず、MKSA有理単位系を基礎とした国際単位基準で解析して、その関係式に実用単位の数値を換算係数毎代入する方式が確実である。換算係数とそのデータを分離して特殊な係数を次々生む計算方式は余程常用性・汎用性のある式以外は避けた方が良い。（運輸省令の計算式はこの「特殊な係数」による方式が多く、鉄道現場のものであるが、一般人向けにはSI基準の方が理解しやすいことが多い。理由に関わらず値を得るために「公式に代入する」立場ではどちらの式も変わりない）
　　1 [km/h/s＝1000m/(3600s)/s＝(1/3.6)m/s2]＝1/3.6 [m/s2]、
　　1 [m/s2＝(km/1000)/(h/3600)/s＝3.6 km/h/s]＝3.6 [km/h/s] ………(3)

　　 【ニュートンの第２法則】　<N>

　加速に要する力Fは、質量Mと加速度αに比例するというのが「ニュートンの(第２)法則」であった。これを数式で表せば、
　　F＝ｋｍα　（ｋは比例定数）であるが、ｍ＝1 [kg]、α＝1 [m/s2]として、ｋ＝１とする力の単位を[N(ニュートン)＝kg･m/s2]として定義して、常用(実用)単位である重量による力：kg重＝kgw＝kgf と分離した。[g][cm]単位で定義した力は、同様に[dyne=g･cm/s2]ダインであり、物理学の一部や材料系で主に用いられたcgs単位系であるが、電気工学と相性が良く実用単位にも共通部の多いMKSA系の有理単位が次第に主流になり、拡張して国際単位SIとして制定された。
　　F＝ｍα ………(4)　　が基本式である。
　　1 [N≡kg･m/s2＝1000g･100cm/s2＝105g･cm/s2]＝105 [dyne]………(5)　　である。

　　 【重力加速度】　<G>

　重力による加速度Gは約9.81 [m/s2] だから、
1 [kgf＝kg･(9.81)m/s2]＝9.81[N]＝981cm/s2･1000g＝9.81×105[g･cm/s2≡dyne], (981cm/s2＝1 [G]) ………(6)　である。
　なお「有理単位」というのは、湧き出し量を全空間の立体角４π[ステラジアン]で正規化して、１[ステラジアン]当たりの量で扱う単位系を言う。
　立体角１ステラジアンというのは、中心から１単位長離れた球面上の１平方単位長を見込む角を言う。１ｍ基準であれば１ｍ離れた球面上の１ｍ2を見込む立体角を１ステラジアンと定める。球面の全面積は４πｒ2であるから、立体角の最大値は４πステラジアンとなる。
 物理では４πで割らない非有理単位系も用いられていた。

　　 【加速度≡速度変化率、速度≡位置変化率】　<α>

　加速度αというのは、時間軸に対する速度Vの変化率、速度Vは時間に対する位置Xの変化率である。
「等加速度運動」というのは、加速度≡速度変化率が時間に拠らず一定ということで、速度V＝加速度α×時間tである。
　　V＝αt＋V0 ………(7)
　(7)式で時間tに対する変化率は、初速V0が一定で変化しないから、α一定ということになる。
例えば起動加速度が１m/s2＝3.6 km/h/s の電車の発車10秒後までの速度といえば、3.6×秒経過10＝36km と直線的に増速する。
c.f.「等加速度運動」との比較のために「等速度運動」を考えよう。速度はV一定で、その位置Xは速度V×時間tである。
　　X＝V･t＋X0 ………(7)-2
　この変化率はVで一定であるから「等速度運動」と呼ぶ。

では、変化率を求めると(7)式になる原式はどうなるか？
　変化率を求める毎に、独立変数の次数が係数に掛かり、次数が１だけ小さくなるから、その逆の操作を行えば原函数を求めることができる(＝積分操作)。それを(7)式に適用すると、
X＝(1/2)αt2＋V0t＋X0 ………(8)
確認法は、(8)式の変化率を求めると(7)式になることで行えば良い。

　変化率f'(t)の定義としては、Δtを無限小に接近する微少値として、
f'(t)＝limΔt→0｛f(t+Δt)−f(t)｝／Δt ＝limΔt→0｛f(t)−f(t−Δt)｝／Δt………(9)
が定義で点tに於けるグラフの勾配だから、
f(t)＝αt2 であるとき、
f'(t)＝limΔt→0｛α(t＋Δt)2−αt2｝／Δ
　　 ＝limΔt→0α｛t2＋2Δt･t＋Δt2−t2｝／Δt
　　 ＝limΔt→0αΔt｛＋2･t＋Δt｝／Δt
　　 ＝limΔt→0α｛＋2･t＋Δt｝
　　 ＝2αt
従って、(8)式の変化率を求めると、(7)式になる。

(7)式のtを→(8)式に代入整理すると
　　2α(X−X0)＝V2-V02 ………(10)
　　　　　 2αX＝V2 ……………(10)-2
この(10)-2式は初速V0＝0の場合の先出現場常用式である(1)式を基本単位で表したものである。
すなわち、X＝L＝Ｖ2／Ｋ＝v2／２αであり、V＝3.6v であるから、 （注Ｖ[km/h],v[m/s],α[m/s2]）
　　(3.6v)2/K＝v2/2α
　　K＝2*3.62α＝7.2*(3.6*α）
　………(3.6*α) は km/h/s単位の加速度である。
それに更に7.2を乗ずるとKになることが分かる。………(10)-3

この換算により減速定数と加速度混在の計算が可能となる。

　実際の数値を当てはめる。
まず、電車・気動車の標準的非常制動加速度(負数は減速度)−4.0km/h/sを、減速定数Kとβm/s2とに換算すると、K＝4.0*7.2＝28.8、β＝−4.0/3.6＝−1.1111m/s2 となる。
　次に、制動定数K＝20/0.7、　20、　15の常用減速度km/h/s、加速度αm/s2を求める。
　　K＝20/0.7＝20/0.7/7.2km/h/s＝3.9583km/h/s＝−1.1023m/s2
　　K＝20＝20/7.2km/h/s＝2.7778km/h/s＝−0.77160m/s2
　　K＝15＝15/7.2km/h/s＝2.0833km/h/s＝−0.57870m/s2

　なお、電車・気動車の標準的非常制動加速度(負数は減速度)−4.0km/h/s というのは鉄道事故調査委員会が試算に採用した値であり、実際には制動初速と車種に拠ってかなり異なるから、その補正が必要な場合もあるが、最近の通勤車両によくみられる値である。京成3100仕様資料掲載の制動特性グラフでは3.5km/h/s〜3.0km/h程度と読み取れるが、140km/hから600m制限で停まれる車両では4.5km/h/s以上の減速度がないと絶対に停まりきれない。新幹線では速度ランク毎に減速度が制定されているくらいだから、更に正確な推定には実車特性と天候などのデータで補正することが必要だ。

tanθ-sinθ比較×1000
勾配
tanθ 		1000
*sinθ 		角度
[度] 		誤差％
5 5.000 0.286 0.00
1010.000 0.573 0.00
1514.998 0.859 0.01
2019.996 1.146 0.02
2524.992 1.432 0.03
3029.987 1.718 0.04
3534.979 2.005 0.06
4039.968 2.291 0.08
4544.955 2.577 0.10

　　 【勾配加速度補正】　<tan>

　勾配加速度Aが直に影響する。勾配角をθ、重力加速度をGとすれば、勾配はtanθで表しているので、Aの値は
　　A＝G･sinθ≒G･tanθ　∵微少角のため。右比較表参照。………(11)
この誤差であればsinθをtanθで代用して良いことが分かる。 加速度・減速度の勾配補正加算時に特に単位換算に注意。m/s2に3.6を乗じると km/h/s、さらに7.2を乗じて制動定数Kとなる。

運動量保存則と完全非弾性衝突　<MV>

　運動物体の速度V×質量Mを運動量と言い、２物体が衝突衝突した場合の総運動量は、衝突の前後で変わらない。
しかし衝突前後の相対速度は条件で異なり、その衝突前後の比率を「反発係数ｅ」という。
衝突後も相対速度が保たれるもの：ｅ＝１の場合を「完全弾性衝突」と言い、この場合運動エネルギーも保存される。
衝突後相対速度がゼロになるもの：ｅ＝０の場合を「完全非弾性衝突」と言い、衝突で運動エネルギーが失われる。
　鉄道の衝突では、東中野も宗像海老津も双方の列車が破損して食い込んで離れない「非弾性衝突」型であった。
　基本関係式は、次の２つである。
　　　M1V1＋M2V2＝ M1V'1＋M2V'2 ………(運動量保存則)………(12)
　　　V1−V2＝−ｅ(V'1−V'2)　　………(13)
ここで ｅ＝0、すなわち V'1＝V'2＝V' ………(完全非弾性衝突)であるとき、(12)式より
　　　M1V1＋M2V2＝ (M1＋M2)V'　であるから
　　　V'＝(M1V1＋M2V2)／(M1＋M2) 　………(衝突直後の速度１)………(14)
先行列車が停止していた場合は V2＝0 であるから(14)式は更に、
　　　V'＝{M1／(M1＋M2)}*V1 　………(衝突直後の速度２)………(14)-2
となる。東中野事故のように停車中の10両編成に10両編成が追突した場合、追突速度の１／２が追突直後の速度であることを示す。また宗像海老津事故での概算は、停止車両が7両、追突車両が5両だから、追突前後の速度比は 5／(7＋5)＝5/12＝0.41667 である。共に停止位置から逆算した衝突直後の速度が判ると、その速度比から衝突速度が算出され、それ以前の走行も推定されることになる。

時素式速度照査地上子計算　<Timer>

　時素式の速度照査には地上時素式と車上時素式がある。
　地上時素式は車両検出地上子と非常制動地上子の間を地上タイマーの設定時間内に通過した場合に過速度として非常制動や警報を発する方式を言い、ATS-Sでは警報(130kHz地上子)、ATS-SNでは非常制動命令(123kHz地上子)を発する。国鉄JRで使っているATS-S系速度照査では地上子設置位置も、時素も共に設定値なので、外形から設定を知ることはできない。京王の過走防止装置は地上時素式とみられ、１型で時素１秒、２型で時素0.5秒固定と思われ、設定状況が推定できる。(See→京王の過走防止装置)
　車上時素式では、２個の地上子間の内法(うちのり)の距離を車上時素設定以内で通過すると過速度として非常制動を掛けるものである。ATS-ST系の速度照査がこの方式で、その時素は0.5秒が標準、貨物列車で0.55秒、JR九州の振り子式特急で0.45秒としている。
　地上子設置ピッチをL[m]、地上子検出幅をW[m]、時素をT秒とするとき、制限速度設定Vは
　　V＝(L−W)／T×3.6 [km/h]　となる。

　時素式速度照査での過速防御の場合は、その考え方により設置位置が異なるが、個々地上子対の速度照査設定時に特に注意することは、その速照地上子対で停止コマンドを受けて停止する速度と制動距離は、その前段のものであることが特に重要だ。例えば速照対設定がYG現示75km/hだった場合の設置位置は、前段の速度照査値か路線の最高速度が95km/hだとしたら、その95km/hで非常制動が掛かった場合に制限地点までに安全範囲に減速できる位置に設置する必要がある。

　この点でJR東海自慢のATS-ST過走防止装置は重大欠陥設定である。それは運転士がY現示速度(45km/h〜55km/h)まで手動で減速している前提で過走を防止するものだから最も危険な高速側が無防備で宿毛事故のように120km/hで突入されて全く防御できなかった。この装置は待避線・副本線用で設置されている分岐器過速度防止装置を直線側本線でも併用しないとほとんど安全装置の意味を成さない素人騙しのオブジェである。

　ところが、物理的機能はJR東海過走防止装置と全く同じ、京王と小田急の過走防止装置は25km/hに減速するまでは信号現示速度照査で減速されてから動作するので有効だ。
　国鉄JR系は安全装置の機能基準についての考え方が間違っていて労災防止の労働省基準とは懸け離れているから、重点を押さえずモグラ叩き対策で次々と事故を起こしているといえる。この基準については厚生労働省の労災防止関係部局が噛んで基準を検討する必要があるのだが、何をしているのだろうか？

　時素型速度照査は２〜３通りの考え方で設置設置されている（様に見える）。 　３番目は、乗務員のエラーがない前提での懲罰遵守型であり危険な高速域が野放しの−ＳＴ型過走防止装置以上に絶対に安全装置ではないが、宿毛事故時の25km/h分岐器制限は減速距離がゼロで防御には全く役立たずこの違反ネズミ取り型設置である。土佐くろしお鉄道ではJRとは違い懲罰日勤教育は無いようだが、これが結構設置されていたのをみると国鉄JR標準型の設置だったから設計施工の鉄建公団も疑問無く踏襲した疑いすらある酷いものだ。なお、信号ATSは運輸省の事前審査と設置後の検査があるが、速度照査は義務付けが無く認可や審査の対象になっていなかった。

　　See→東中野事故解析図
東中野事故推算
　　See→宗像海老津事故解析
宗像海老津事故推算

計算演習　<study>

　解析方法が判っていても、実際に適用となるとかなりまごつくもの。誰でもピアノの鍵盤を押せば音が出るのは判っているが、練習しなければメロディーにはならないのと同様、解析も慣れていることが深く正確に取材する上にも必要だ。以下の解析例リストも辿ってみて戴きたい。

試算例と事故調報告
#解析例Date報告書等
0事故記事リスト 02/02/ [鉄道事故調報告書]
1 鹿児島線宗像海老津事故 02/02/22 事故調03-4B-1
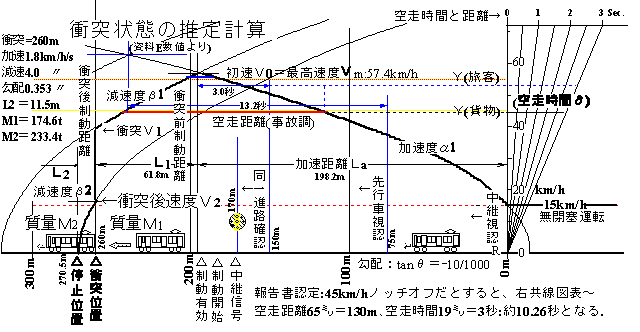
2土佐くろしお鉄道宿毛事故 05/03/02 事故調RA07-4-1
3 　〃　EBで制動か？最終報告
4福知山線尼崎事故 05/04/25 事故調RA07-3-1
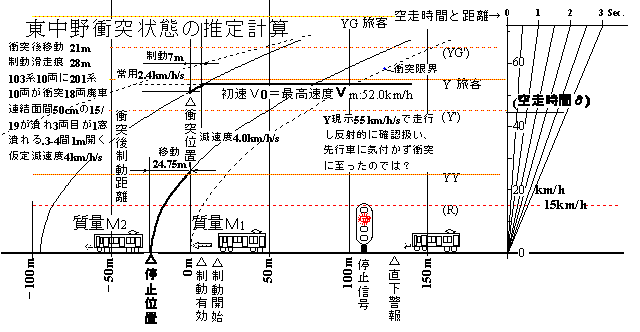
5中央緩行線東中野駅事故 88/12/05 千葉支社通達
6京王井の頭線吉祥寺過走事故 05/04/21 (日記117)
7西鉄大牟田線津福誤出発 09/03/01 (未公表)非着手？
8東急元住吉ATC雪中追突 14/02/14 RA2015-3-3　 資料
9TGV試験運転転覆事故 15/11/30 −
10JR高徳線オレンジタウン誤出発脱線事故 15/12/31 調査中

衝突解析計算を誰もが可能に　<pos>

　衝突状況が推算できる詳細な数値報道が次第に行われる様になったのは1988年12月5日発生の中央緩行線東中野事故辺りからで、97年の中央線大月事故、東海道線片浜事故、2000/03/08日比谷線中目黒事故は数値の絡みが弱く、'02/02/22鹿児島線宗像海老津事故ではネットBBS情報が大きく、'05/03/02土佐くろしお鉄道宿毛事故、/04/25福知山線尼崎事故から推算可能な数値データが報道されるようになった。
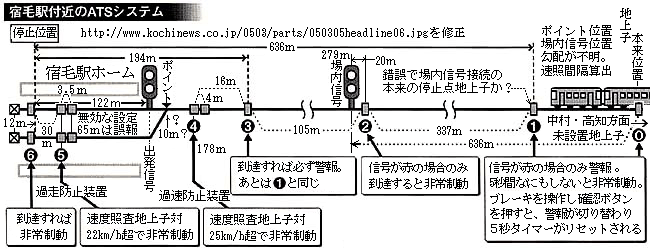高知新聞宿毛駅地上子位置050305headline06.jpg
'05/03/05高知新聞記事図補正 　事故防止限界算出可能＝事故状況推定可能の優れた記事↑


[衝突解析例] '02/03/01作図
　しかし、読売新聞のK機長説など根拠のない憶測や、目眩ましの「133km/h以上で脱線する」転じて「133km/h未満の脱線には過速度以外の原因がある」とするデマは無批判に並べ立てても、その具体数値を引用した試算記事は無く、試算前提の評論すら見られず、結局は事故調査委員会発表待ちでの報道に留まっている。

　公的な資料での詳細試算公表は日比谷線中目黒事故での事故調査検討会報告書資料が最初で、尼崎事故調報告が更に詳細な報告を行っているが、宗像海老津事故では主因でないためか試算がかなりルーズだったし、宿毛事故では運輸省のATS-Sx地上子設置基準そのものに問題があって、詳細計算は記載しないことで設置基準欠陥を表面化させずに蓋をし、各翌'06年3月に鉄道事業者責任とする技術基準制定を行った。線路状況に応じた安全装置の選択・不設置は事業者の責任と判断で行うものとして、万一事故になっても監督庁には責任がないというずる〜〜い改訂を潜ませている。

　しかしながら、衝突事故やATSの解析はさほど困難なものではなく、加速・減速運動と、衝突計算にほぼ尽き、高速領域を含む解析で例外的に区分求積法が用いられる程度だから、中学3年〜高校1年で2次方程式を学んでおり若干高度の文章題（＝昔は「応用問題」）として順を追って説明されれば一般人にも充分計算可能で、それにより有力な推論を導けるものである。解析手順さえ分かっていれば、事故調中間報告が出たらその数値データを元に各自正確な推算ができるし、そういう単純数値データの取材はマスコミならたやすいはずだから、事故直後の独自解析は本来可能である。それを示す最も典型的な例が宿毛事故での高知新聞の地上子位置報道（上図参照）だったし、東中野事故での毎日新聞などの詳細な位置報道だったが、残念ながらその具体数値群が内包する情報を抽出して「数値から解析するとこうだったはず」とする分析的報道まではされなかった。

　「専門」が絡むと都合の悪い事実が隠されて誘導されてしまうことが少なくない。宿毛事故でのATS地上子設定基準のエラーなどそれを制定認可した運輸省自体のエラーなのに全く追及されてないし、国鉄の当事者調査だった時代には「続・事故の鉄道史」などに暴露されたような隠蔽が重ねられている。ワラ１型試験省略で欠陥を見逃して発生した鶴見も「競合脱線」の原因不明論で交わされ、適切なトンネル火災対応を不当処分で厳禁して惨事化した北陸トンネルも不運な乗務員の刑事裁判、重連対応の中継弁設置を放置、運転通告券非発行、同時進入制限不実施などの怠慢に目をつぶり乗務員の信号誤認(あるいは駅員の信号操作遅れ)が原因とした参宮線六軒も、重要な原因が伏せられたままの処理に終わっている。尼崎事故でのJR西日本の口から出任せの様な責任逃れに誰もが信用しなくなり「ATS-Swでも速度照査可能で現に17個所に設置している」という技術的内容の発表にも他への裏取り取材がされ、記事にしなかった社が多かった。

　こういう状況打破には、事故状況を試算、解析できる人達を激増させて、それぞれが様々のサイト、ブログで試算・公表して、一般的状況認識＝公知の事実を形成させてしまうことが有効だろう。各自の「主張」が「○○新聞の受け売り」ではなく、物理的根拠に基づく各自自身の解析結果に基づくものにすることだ。計算手順が理解できれば報道から拾うべき数値（＝取材・報道すべきパラメター）も明確に見えてくる。（自分で試算するのなら取材項目を落とさない）。執筆者・取材者にとっても解析方法を理解できていれば１日〜２日の作業だし、当ページの各章を潰しながらの算出でも１ヶ月もあれば結論が得られるだろう。この解析は'88年の東中野事故で始めたものだが、事故の実態が良く分かる。
　物理計算の裏付けのある主張ならJR西日本の見解「133km/h以上で脱線（＝それ以下での脱線には過速度以外にも原因があり、JR西だけの責任ではない）」や、川島某氏などの御託宣を中和・解毒できるようになるし、括弧付き「識者」も好い加減な評論を振りまけなくなるだろう。

2009/03/25　23:55
[Page Top↑] 戻る
前 		LIST
主目次 		Diary INDEX
日記list