JRQ鹿児島本線
【03/08/29 事故調報告書の検討】
追突事故の直接原因は、(先行列車が同一区間内に在線する)無閉塞運転中に中継信号の進行現示で加速したエラーであることは間違いないが、物理的にどのような経過で衝突に至ったかの解析については幾つかの点で重要な異論があり、その解析に説得力がない。報告書の事実認定は、事故現場に残された直接の値と、運転士の供述を軸にしている。
(1).その供述中に物理的に背反する供述があるが、その片方を採用し、もう一方を捨てた理由を述べていない。すなわち「加速して45km/hに達して、無意識でノッチオフした」というのと、「下り坂で加速され55km/h近くに達したと思う」というのは両立せず、55km/hに達するにはフルノッチのまま加速を続けて、先行列車に気づいて非常制動をかけた場合だ。
両方とも運転士の供述だから、事故で記憶が混乱したり、会社の当初の主張に引きずられている可能性があるから、どちらを採用し他を棄却するかは、他の客観的な事実との整合性から判断されるべきだ。ところが報告書はノッチオフ説採用の理由には全く触れていない。
また、衝突速度の推定(付属資料E)に総運動エネルギーを用いている。
(2).その中で、衝突変形損壊によるエネルギー消費(E3)をゼロにして衝突状態を推定している。その値に過去の実験データから推定の車両端面あたりの衝突損失を加えている。 しかし、報告書に述べられる事故状況は反撥係数ゼロの完全非弾性衝突と見受けられるから、衝突損エネルギーは直接に算出可能である。この値に対して理由ある補正を加える方が順当だと思う。
(3). 衝突後に失われた運動エネルギーの推算は、衝突後移動距離11.5mを、先行車はレールとの摩擦係数μ=0.3で、追突車は減速度4.0km/h/s−10/1000勾配加速度の力でそれぞれ減速されたとして放出エネルギーを計算している。
しかし、静止摩擦も一旦動き出せば小さくなり、一体で動く衝突車と同律になると考えるべきだろう。先行車ばかりが大きな抗力を負担するとは考えがたい。
<calc> 以上の点をふまえて衝突状態を再計算する。
(2).項の影響が大きいから、基準値を算出する。
運動量保存則より
| 追突車質量M1・速度V1+先行車質量M2・速度V2 | =M1・追突直後速度V1’+M2・直後速度V2’ | … (1) |
| −反撥係数e(V1−V2) | =(V1’−V2’) | … (2) |
V1’=V2’=V3とすれば
| M1・V1+M2・0 | =(M1+M2)V3 | |
| V1 | ={(M1+M2)/M1}V3 | ………… (3) |
|
衝突直後のエネルギーE1・2は | ||
| E1・2 | =(1/2)(M1+M2)V3^2 | ………… (4) |
|
衝突前の運動エネルギーE0は | ||
| E0 | =(1/2)M1・V1^2 =(1/2)M1・[{(M1+M2)/M1}V3]^2 | |
| =(1/2)[{(M1+M2)^2/M1}V3^2] | ||
| ={(M1+M2)/M1・[(1/2)(M1+M2)V3^2] | ………… (5) | |
| ={(M1+M2)/M1}・E1・2 | ………… (5)’ | |
| 衝突前後の運動エネルギーの減少が衝突に費やされたエネルギーEcだから | ||
| Ec | =E0−E1・2 ={(M1+M2)/M1}・E1・2−E1・2 | |
| =(M2/M1)・E1・2 | ………… (6) | |
| =(M2/M1)・(1/2)(M1+M2)V3^2 | ………… (6)’ |
付属資料Eで求めているエネルギーは(衝突で失われるエネルギーをゼロとしているので)衝突直後の値と解されるから、これから衝突直後速度を求めると
| V3 | =sqrt(2E1.2/M)=sqrt(2×9.6 ×10^3k/406.0t)×3.6=24.76 km/h | |
| Ec | =(233.4t/172.6t)(1/2)(233.4t+172.6t)V3^2 | |
| =(233.4t×406.0t/2/172.6t)(24.76/3.6)^2=13.00[MJ]=E3 | ( … (6)'より) |
Ek=E1+E2+E3=7.6[MJ]+2[MJ]+13[MJ]=22.6[MJ]
この値から衝突速度V1を計算すると
V1^2=2Ek/M1=(58.23/3.6)^2 ………… (衝突速度がかなり高い!)
(3).事故調査報告書採用数値の点検
値を良く眺めると、衝突後の減速エネルギーが、5両で2[MJ]に対して、7両編成で7.6[MJ]というのがいかにも大きい。その根拠を洗うと、E2は非常減速度見合いの制動力4.0km/h/s−勾配だが、E1が最大静止摩擦0.3−勾配が滑走中持続したとして計算されている!滑走を始めれば摩擦力は大幅ダウンするから、恐らくここが誤差発生原因になっている。先行車の滑走開始時の一瞬を除いた滑走時の摩擦力は、追突車の非常制動の抗力に等しいと考える方が無理がない。すなわち
| E1+E2 | =233.4t×(1.11−0.01×9.8)×11.5+172.6t×(1.11−0.01×9.8)×11.5 | ||
| =2.72+2.01 [MJ]=4.73 [MJ] ……… 半分以下となる! | |||
| V3 | =sqrt(2E1.2/M)=sqrt(2×4.73 ×10^3k/406.0t)×3.6=17.38 km/h | ||
| Ec | =(233.4t/172.6t)(1/2)(233.4t+172.6t)V3^2 | ||
| =(233.4×406.0t/2/172.6)(17.38/3.6)^2=6.40[MJ]=E3 | |||
| Ek | =E1+E2+E3=2.72[MJ]+2.01[MJ]+6.4[MJ]=11.13[MJ] | ||
| この値から衝突速度V1を計算すると | |||
| V1^2 | =2Ek/M1=(40.88/3.6)^2 ………… 妥当な衝突速度! | ||
これはまた、運動量保存則と減速度から試算したものに一致する。
各種推定は、以上の状態を基本にして、細々の事情で修正されるべきであり、基準点のない修正では匙加減次第になってしまうから極力避けるべきである。
(1).さて、45 km/hでのノッチオフがあったかどうかの判定には、ノッチオフの惰行が全くなかった場合の走行曲線を上限に、ブレーキ操作時の不動時間、45km/hなど特定速度での走行曲線を描いて突き合わせる必要がある。
改良線路での旅客列車のY現示速度制限は55km/hであり、45km/hではない。貨物列車の速度制限が旅客運転に出てくることはないから、証言で繰り返される「無意識のうちに○○した」という部分が記憶の混乱や他者の意向の反映など信用性を疑わせてしまう。無意識の行動としては警報持続装置のリセットと、45km/hでのノッチオフである。
[加速限界点の算出]
上記の最高速度をVm、衝突直前速度をV0、加速開始時速度をV00、減速度β、加速度α、勾配をtanθ、加速開始位置−衝突位置間距離をD、減速距離をL1、加速距離をLaとして
Vm、La、L1を求めると
| D | =La+L1 | ……… (7) |
| Vm^2−V00^2 | =7.2α・La | ……… (8) |
| Vm^2−V1^2 | =7.2β・L1 | ……… (9) が成立する。 |
| (8)−(9) | ||
| (V1^2−V00^2)/7.2 | =α・La−β・L1 =α(D−L1)−β・L1 | |
| =α・D−(α+β)L1 |
| L1 | ={(V1^2−V00^2)/7.2−α・D}/(α+β) | ……… (10) | |||||||||||||
| La | =D−L1 | ……… (11) | |||||||||||||
| Vm^2 | =7.2β・L1 +V1^2 | ……… (12) | |||||||||||||
|
但し、αは勾配tanθ加速度を加算、βはtanθ加速度を減算する。 勾配tanθ=10/1000は、10/1000×9.8×3.6=0.353 km/h/s>
L1 | ={7.2(1.8+0.353)260+15^2−40.88^2}/{7.2(1.8+4.0)} | =61.88 m |
La | =D−L1=260−61.88 | =198.12m |
|
(12)式より、あり得る最高速度Vmは |
Vm | =sqrt{7.2(4−0.353)61.88+40.88^2 } | =57.41 km/h
| | ||||
【付属資料の数値で算出】 (この値は疑問。先行車の摩擦係数0.3が大きすぎ)
L1={7.2(1.8+0.353)260+15^2−58.23^2}/{7.2(1.8+4.0)} =20.71 m
La =D−L1=260−20.71=239.69m
(12)式より、あり得る最高速度Vmは
Vm=sqrt{7.2(4−0.353)20.71+58.23^2 }=62.73 km/h
衝突速度58.23km/hという値は、中継信号進行現示をみてフルノッチ加速をして21m手前から減速したことを示しており、45km/hでのノッチオフはあり得ないことになる。(報告書数値からのこの値は採用しがたいが)
[付属資料E]の試算では、先行車の摩擦係数μ=0.3 が衝突後停止まで作用したとの仮定と、衝突で失われるエネルギーの1.8 [MJ]という数値に無理がある。更には、衝突直前の速度の試算法を衝突計算に依らずに、衝突時に失われるエネルギーをゼロ(完全弾性衝突:反撥係数e=1)として行ったが、それがe=0では適用出来ないため不自然に大きな誤差を生じたものだろう。
<fig2> 以上の計算結果を図示すると以下の通り。
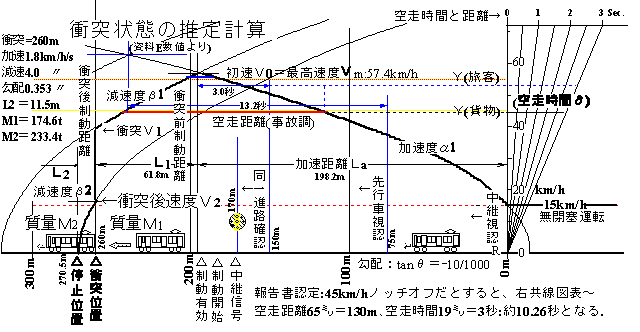
この結果から45km/hノッチオフ供述を採用するか、55km/h到達供述を採用するかを判断。 「同一進路をこちらに向かってくる列車を発見してあわてて非常ブレーキを掛けた」という供述からすると、前者なら同一進路確認点から約94mを空走、後者なら47.9m〜48.2m加速。事態に気づくまで7.4秒なのか?3秒なのか?……、無条件で45km/hノッチオフ説は採れないと思う。
| 運動量保存則からの試算 | 
| 
| 
| ||
|
Last Upload:
:
Last Update=2003/09/06
| |||||