[memo]

BBS
BBS
mail to: adrs
戻る
前 		LIST
主目次

光学系諸定義　（控）

光量[LV値]：[Light Value]　　　 <LV> 　　　See→[目次:<Light>]

LV値（Light Value）
＼F→
↓1/T 		１ 1.4 2 2.8 4 5.6 8 11 16 22 32
T 32s −5 −4 −3 −2 −1 0 1 2 3 4 5
16s −4 −3 −2 −1 0 1 2 3 4 5 6
８s −3 −2 −1 0 1 2 3 4 5 6 7
４s −2 −1 0 1 2 3 4 5 6 7 8
２s −1 0 1 2 3 4 5 6 7 8 9
シ
ャ
ッ
タ
｜
速
度
1/T
↓ 		１ 0 1 2 3 4 5 6 7 8 9 10
２ 1 2 3 4 5 6 7 8 9 10 11
４ 2 3 4 5 6 7 8 9 10 11 12
８ 3 4 5 6 7 8 9 10 11 12 13
15 4 5 6 7 8 9 10 11 12 13 14
30 5 6 7 8 9 10 11 12 13 14 15
60 6 7 8 9 10 11 12 13 14 15 16
120 7 8 9 10 11 12 13 14 15 16 17
250 8 9 10 11 12 13 14 15 16 17 18
500 9 10 11 12 13 14 15 16 17 18 19
1000 10 11 12 13 14 15 16 17 18 19 20
2000 11 12 13 14 15 16 17 18 19 20 21
4000 12 13 14 15 16 17 18 19 20 21 22
２LV＝F2／T,　
　LV＝log2{F2／T}＝２log2F−log2T≒3.32×log10{F2／T}

　絞りＦ数（焦点距離／レンズ開口径）＝１のレンズで１秒間露光した場合の露光面光量を基準値として、絞りFと露出時間Tによる減光比を２を底とする対数で表したものをLight Value：LV値、光量という。
　機材の光感度を表す数値でフィルム感度は要素に入っていない。（近年、この機材特性を表すLV値（ライトヴァリュー）をEV値と呼ぶ向きもあるが、元々はLV値であり、LV値を基準に露出設定するカメラも市販されていた（Ricoh-500シリーズ等）。かってはEVにはフィルム感度など別の要素を加味していたはずだが資料が見つからない。かっての考古学的露出計にはLV値とEV値が別に表示されていたから、それが同値に扱われるというのは、AF全自動カメラ全盛を経て変遷と混乱を生じているものだろう。現在ではLV値＝EV値（Exposure Value）である。See→EV値）

　露光面光量が基準状態と同じになるシャッター速度T、と絞り値Fであるから、LV値はシャッター速度に反比例し、レンズ開口面積に反比例＝レンズ開口径Dの２乗に反比例、Ｆ数（焦点距離f／レンズ開口径D）の２乗に比例し、基準であるF＝１、T＝１の場合が2底の対数表記されて０となる。
　すなわち
２LV ＝F2／T　　　が基本関係式であるから、
LV ＝log2{F2／T}
＝log2F2＋log2(1/T)　…………(暗算用式)
≒3.32×log10{F2･(1/T)}　…………(電卓用式)
　以上の式で(1/T)としているのはシャッタースピードは逆数で扱う方が符号も＋になり楽だからである。２底の対数を求めるのに1/512から−×−より512の方が扱いやすい。数列としてはlog264＝6目盛まで「がまの油売り」の口上であり1024が10乗である。
[例]：1/256→(1/T)→256→28→log228＝8
　レンズのF数も同様にF＝2.8＝2√2 よりもF2＝(2√2)2＝8、　log28＝3 で扱う方が対数なのに整数で扱えて楽だからである。双方の和であるLV＝8＋3＝11 と算出される。
　以上によりシャッター速度と絞りの組合せでのLV値は右表の通りとなる。レンズのF数とシャッター速度の逆数(1/T)それぞれの２底対数値の和がLV値であるが、規格値が2nでその対数が整数なので暗算できる。

[ LV値の速算 ]

　LV値は積の対数だから、和の形になり、シャッター速度(1/T)の2底の対数をタイムバリューTv＝log2(1/T)、絞りの2乗の2底の対数をアパーチャーバリューAv＝2･log2(F)と呼んで、それぞれの和：LV＝Av＋Tv として独立に計算できる。
LVT[1/s]F備考
011基準
121.4
242
382.8
4164
5325.6
6648
712811
8256161バイト
951222
10102432K。絞り限界
112048(44
124096(64
13(8192(88
14(16384(128
15(32768(176
16(65536(2562バイト
17(131072(352
18(262144(512


　2底のlogの算出は、一般的にはlogaB＝logcB／logca により常用対数化して、
　　log2X＝log10X／log102
　　　　　≒3.3220×log10X
　　として算出する。

　実機のシャッター速度Tと、絞りF2は、基本的に2N数列で定義して２倍ごとに＋１となっているため、特定の2N数値を知っていると、その2N〜1／2NかでLV値を容易に暗算できる。

　例えば 210＝1024で、シャッター速度1/1000がTv＝10、1/2000がTv＝11、1/500が、Tv＝9･･････となるし、
　4-20mAカーレント・ループ12ビットADコンバータの0〜4095レベル：計4096＝212でTv＝12、
　１バイト＝8ビット256＝28でTv＝8、
　BASIC整数変数16ビット65536＝216でTv＝16、
　32＝25だから、絞り32のアパーチャーバリューはAv＝2･log2(F) より、Av＝2×5＝10、と、カメラの通常の設定範囲ならLV値を暗算で算出できる。
　なお、右表でKByteは1024Byte、kByteが1000Byteを表すのがメモリー容量などPC内部処理での慣行。KByteはPC外の事象には使わない。

　実例を挙げれば、T＝1/512、F＝16のLv値は、512＝210／2＝29でTv＝9、（16＝24）2 より、Av＝4×2＝8 により、LV＝9＋8＝17 になって、LV表の値になっている。
　製品上ではシャッター速度を10進数に合わせて以下のように若干修正している。
　　　16→15、32→30、64→60、128→125、256→250、512→500、1024→1000、2048→2000、4096→4000
F数解説

[ レンズの明るさＦ ]　　　 <F>

　レンズの明るさＦは、(焦点距離f／レンズ開口径D）で定義され、小さい程明るい。
光量はレンズの開口面積πD2／4に比例するが、結像面での明るさは像の面積によるので無限遠被写体像であれば１／Ｆ2に比例することになる。結像面が基準照度一定では、光量としてはＦ2に比例する。
　結像面でのある像の大きさdはレンズの焦点距離ｆに比例するが、同じＦ数のレンズであれば、開口径Dもｆに比例するので、像の大きさと開口径が比例するから、レンズが同一F数であれば像の明るさは同じになる。マクロ撮影で像が暗くなるのは結像位置が焦点距離より遠くなって光が距離２乗比例で分散し光束密度が反比例するためである。

実照度例

ASA＝100　フィルム感度：(理科年表☆太陽と月５．p52より算出)
状況 [lux] LV値 備考
100W電球直下1m 100. 　 5.3 　裸白熱電灯標準
100W電球直下10m 1. 　 −1.3
直射太陽 200,000. 　 16.3 夏至正午の日向
直射太陽 100,000. 　 15.3
晴天風景 16,000. 　 12.6 （基準) 晴天の順光風景
室内の窓際 1,000. 〜2,000. 10.5 　
室内の真中辺 100. 〜200． 7.1 　
室内の隅 10. 〜20. 3.8 　
LV＝0照度 2. 5 0.0 　(ASA=100)
満月 0. 2 −3.6
夜光 0. 0003 −13.0 　晴天無月の夜
星光成分 0. 00006 −15.3
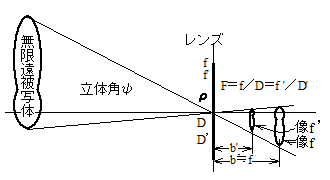
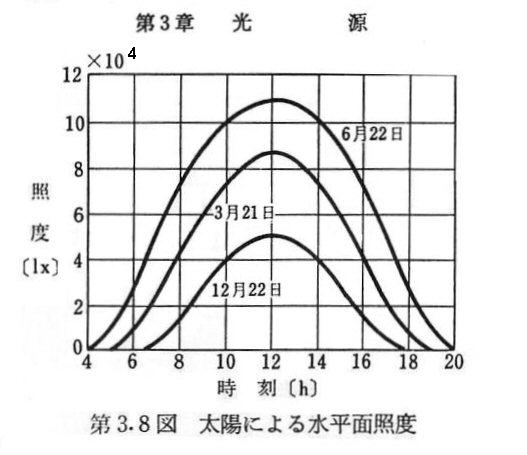照度季節時刻変化
by｢照明工学(改訂版)｣p52
電気学会1978/09/12刊
24刷2000/09/20
初版1刷1963/07/15〜26刷

　光量の１単位段階はシャッター、レンズ共２倍。レンズの開口面積は開口径の２乗比例だから、F数の１単位は√２倍。

　今、F数（焦点距離f／開口径D)の２つのレンズを想定し、一方をＦ＝（f'／D')とし、レンズ面での被写体光による光束密度をρとするとき、総集光量はそれぞれ
　　Φ＝ρ（π/4）D2　　と　Φ'＝ρ（π/4）D’2
結像面の像の大きさは面積で「立体角ψ×半径ｆ2」だから、それぞれ
　　f2ψ　　　と　　 ｆ ’2ψだから
　像の光束密度は　総集光量／像の面積で
　　Φ／f2ψ＝ρ（π/4）（D2／f2）ψ
　　　　　　　＝ρ（π/4）／Ｆ2ψ　となってＦ数で決定。同様に
　　Φ’／f ’2ψ＝ρ（π/4）（D ’2／f ’2）ψ
　　　　　　　　　 ＝ρ（π/4）／Ｆ2ψ　でＦ数で決まり同値となる。
　　すなわちレンズのＦ値で撮像面の像の明るさが決まる。但し像の大きさは焦点の長さ：レンズの大きさに比例するので解像度には直接影響する。

[ 広角レンズvs長焦点(望遠)レンズ ] 　　　<W&L>

　像の大きさが焦点距離に比例することから、同じ大きさのフィルムであれば長焦点の方が大きな像が得られて「長焦点レンズ」と呼び、逆に短焦点であれば写角が大きくなってそれを「短焦点レンズ」ではなく「広角レンズ」と呼ぶ。
　文字通りの「短焦点」では一眼レフカメラの場合ミラーがレンズに当たってしまうので、後述「望遠レンズ」の逆補正をして鏡筒の長さを伸ばしているため敢えて「広角レンズ」と呼んでいる。

　35mmカメラでいえば、焦点距離は「標準レンズ」が50mm前後（45mm:Ricoh〜55mm:Olimpus）で、これより長いものを長焦点レンズ、短いものを広角レンズ（短焦点レンズ）と呼んでいる。市販品で75mm、135mm、200mmは長焦点、35mm、27mm、24mmは広角レンズである。

　焦点距離を連続的に変更できるレンズを「ズームレンズ」と呼ぶ。ズームレンズの（最長焦点距離／最短焦点距離）を「ズーム倍率」と呼び、最近では広角〜望遠までをカバーする３〜２０倍程度が市販されているが、銀塩カメラ時代にはポートレート用などとして50mm〜75mm、75mm〜135mmといった可変範囲の狭い製品が主だった。

[ 画角：（画面幅/焦点距離） ]　　　<θ>

　デジタルカメラでは、銀塩カメラと同じレンズを装着できる１眼レフカメラでも撮像面が35mmフィルムの2/3程度の大きさ(APS-C規格)なので、その画面寸法を基準に「35mmカメラ換算」で話をすることが多い。200mm−18mmズームは35mmカメラ換算で300mm−27mmズームに相当するという訳である。高級品には35mmフィルムサイズの撮像素子のものもあるが、非常に高価。

　撮像素子が35mmフィルムより小さいことを逆用して、１眼レフカメラの交換レンズを「デジカメ専用」に設計したものが近年は主流化している。35mmカメラと同一マウントだが、均質に結像する範囲を撮像素子に合わせて小さくして低価格化を図るものである。画像はレンズの中心から離れるに従って暗くなるから大口径が必要とされたが、撮像面が小さければその分レンズを小型にできるためである。
　コンデジ（コンパクト・デジタル・カメラ）やAPS-C規格カメラの焦点距離表示で「標準レンズ換算200mm」といった表示が行われている。その意味は、画角が、標準とされるカメラでの画角と同じになる焦点距離を言っている。 現在の標準カメラは35mmフィルムを用いた焦点距離50mmのカメラを基準にして、そのレンズの焦点距離に換算することで画角の目安としている。（上図参照↑）
　APS-C規格のカメラの撮像面幅幅は24mm前後（メーカーにより微妙に±）だが、これは標準のカメラの撮像面幅が36mmだから、同じレンズを使って、画角が2/3になる。すなわち36mmカメラでその逆数である3/2倍の焦点距離のレンズを使ったのと同じ画角になるので、「焦点距離200mm（300mm相当）」とか「18−200mmズーム（27−300mm相当）」といった表記になるものである。

[ 長焦点レンズvs望遠レンズ ]　　　<Long>

　「長焦点レンズ」も「望遠レンズ」も機能で見れば同じものであるが、凸レンズと受光面の間に凹レンズを加えることで鏡筒長を焦点距離より短くした長焦点レンズを特に「望遠レンズ」と呼んでいる。「広角レンズ」では逆に鏡筒長を焦点距離より長くして一眼レフカメラのミラー取り付けスペースを得ている。

[ 絞りと焦点深度と光の回折 ]　　　 <D>

　F数が大きくなると、焦点を結ぶ範囲＝焦点深度が広くなる。右写真でカメラレンズの距離指針の両側にF数を刻んでいるのは、その表示の範囲で実用上焦点が合っていることを示していて「焦点深度表」と呼んでいる。右写真の例では、約2.5mに焦点を合わせているが、焦点深度表から読み取ると絞りがF=8の場合、距離2m〜3mの範囲の被写体にピントが合い、F=16では1.8m〜4mの範囲にピントが合う（＝範囲外は惚ける）ことを示している。

焦点深度表：オリンパスＭ−１ＭＤ改
　１眼レフカメラではファインダーを覗きながら実際に絞ってみてどの範囲にピントが合うか視覚として確かめることができるから、絞りを開けて（その分シャッター速度を速くして、あるいは減光NDフィルターを装着して）被写体以外の後景・前景を暈かしたり、逆に絞って全体に焦点を当てる撮影を選べる。
　撮りたい被写体のみに焦点を当てて、他を背景として暈かし被写体を強調する撮り方は人物写真（ポートレート）に良く使われる手法で、一部に「一眼レフ写真」などと呼ぶ向きも居られるようだが、実際はレフカメラでなくても焦点深度表を見て撮影可能。直接覗いて背景の惚け具合を確かめられる簡易さがレフカメラの特長である。（２眼レフも「視差」以外は同様だ）
　一方、観光絵葉書写真とか各種記録では視野の総てに焦点を当てたいこともあり、特定の被写体を強調するのとは対極の撮り方で、それは撮影者の意図による選択である。「写真」と呼ぶからと言って、総て「真」を写せばいいとは限らず、補正ソフトによっては「輪郭以外を暈かす」という機能があるが、それは皺消しや汚れ消しに使うもの。アナログテレビの様に画素数が少ない絵ではピントを心持ち甘くして皺を見えなくしていたが、解像度の高いデジタル化で補正に苦労する様になった。
　　　（2012/04/04一部補足）
　被写界深度のサンプルとして次のサイトを挙げておく。背景のボケ具合を比較してみて欲しい。See→[サンプル写真]

　しかしながら、カメラの実機ではF22〜F32が最大。その理由は絞り径を小さくすることでF数を増やすと光の回折現象で像が甘くなるため実用範囲に留めているため。F32の光量はF1の1/1024（＝322＝(25)2＝210）10段階であり、普及機のF2.8〜F22なら６段階1／26＝１／６４が調整範囲である。

[ レフか？非レフか？ ]　　　<REF>

　一眼レフカメラの普遍的な欠点は、撮影時にファインダーミラーを跳ね上げて露光させるためその等価質量反比例の回転振動がカメラボディーに起こり、解像度を落とすこと。しかし、それを言ってしまうと絞りを閉じる回転運動の反作用で画面が捻られる影響も出ているはずで、影響度の判断にはデータの欲しいところ。それなのに片方しか採り上げられないのは何等かの意図をも疑って話半分にみた方が良い。その振動回避に、手動でミラーを上げるノブの付いた機種もあるが、撮影の機動性を欠くことになるし、手動を省略している機種では対応が取れない。高級機にはミラー上げとシャッター動作間に遅延時間を設定してミラーによる振動の影響を回避する機種もあるが、それは連写機能を殺すことになる。右上写真のオリンパスM-1／OM-1では手動ミラーアップ可能だが、後継機種のOM-2では省略されている。
　これを避ける構造として、ミラーは動かさずに透過型としてファインダーに光を導いたり、ミラー無しで電気的なディスプレー画像をファインダーに表示する機種＝ミラーレス一眼が現れたが、問題は直射日光下での扱いで、ファインダー／モニター像は一眼レフが格段に見易く、ディスプレー方式では到底追い付かないし、さらに背の液晶画面を直接見る方式では見えにくくて使い物にならない 。
　個人的には可動部のない透過方式レフ・ミラーの機種に興味を惹かれているが、振動抑制に卓効があるかどうかは別で、現実的には高速連写毎秒10〜12コマを連続AF（自動焦点）で撮影できるという驚愕の鉄ヲタ写真仕様に特長が現れるとか、それがSONYではミラーレス指向が強く見えて、いつ転進して切り捨てられるか判らない不安が残っても、今現在使いたいという「機能優先」の機種選択もあり得る。近年、ディスプレーの表示速度に遅れはあまり感じなくなったが、直射日光に負けない高輝度のディスプレーはまだ無理のようだから、簡易コンデジ系は携帯電話付属カメラに吸収され、独立のカメラとしては透過ミラー式が残るのか、ミラーレス一眼としてディスプレー式になるのか？あるいはまた従来の可動ミラー式が生き残っていくのか予測判断が難しい。
　　　（2012/04/04補足）

[ フィルムの感度／絶対感度 ]　　　<ASA>

【ISO-DIN
フィルム感度
対応表】
#ASA
ISO		DIN
01/1.280
11/0.643
21/0.326
31/0.169
412.512
52515
65018
710021
820024
940027
1080030
11160033
12320036
13640039
141280042
　　外部サイトSee→[ フィルムの絶対感度定義 ]
　旧来のASA（=JIS）感度はANSIを経て、現在ISO感度となっており、対数定義のDINは露出計算に使わないためか見掛けなくなっている。ISO-DIN換算は、ASA＝JIS＝ISO 100＝DIN 21で、対数のDINに３が加わる毎にISOが２倍になる。逆換算は、ISOの２倍毎に、対数のDINに３が加わる。すなわち、
　　　　DIN＝10・log（ASA×1.28)≒10・log（ASA)＋１
　　　　ASA≒10（DIN−１)/10　となる。
　フィルム感光は、対数光量と現像濃度がほぼ比例する領域があり、上端が飽和、下端がノイズのＨＤ氏曲線と呼ばれる特性になっている。（See→下図Osc）
　フィルム感度の定義は、被りベース濃度＋0.1濃度を最小値基準に定めて、光量で20倍を露光した時の濃度が最小基準＋0.8となるように現像して、0.8を先の最小基準光量で割った値をフィルム感度Sと定義する。最小基準光量が0.008 Lux秒であれば感度S＝0.8/0.008＝100と定義される。（との主旨の解説だが、残念ながら「濃度」の絶対定義解説が見あたらない。被りベース濃度＝ノイズレベル）
　　　（2012/04/04補足）

［ 平均測光、点測光 ］
　　オシロスコープ写真の名人　　　<Osc>

ダイナミックレンジ 　写真の露出決定というのは、受光面の最大受光値から最小受光値までの範囲に画像各点の明度が収まるよう調整することであり、その受光範囲を銀塩フィルムでは「ラティチュード」と言い、デジカメでは「ダイナミックレンジ」｛＝10・log (最大値／最小値）[dB]｝と呼んでいるが、これが銀塩フィルムの方がかなり広い上、露出が少ないことが分かっていれば「増感現像」をすることで、実質は更に範囲を拡げることができる。失敗の許されないプロユース、報道ユースで銀塩カメラが支持されてきた基本的理由はこのラティチュードの広さの問題だろう。二度とない一瞬のシャッターチャンスを生かす現像は銀塩フィルムの方が使用範囲がずっと広いのだ。
　一方デジカメは確かにダイナミックレンジは銀塩に比べれば非常に狭いが、その場で撮影状態を確認でき、プリントアウトやWeb転送、画像データとしての使い回し、データ管理が大変やりやすいので、繰り返し撮影が可能な被写体でデジカメの演色性に満足できるなら、圧倒的にデジカメ有利であり、一般向け市場はかなり前にデジカメが席巻した。

　画面の撮影データ：露出を決定するに際して、画面全体の平均照度を基準に採る「平均測光」か、特定の被写体の平均照度を基準に採る「スポット測光」「中心測光」かという問題があり、カメラ（内蔵露出計）はそれを設定できるようになっている。さらに高輝度被写体など「露出計では直接対応できない領域」もあり、その対応法が必要だ。なお、撮影用レンズを通して測光する方式をTTL（Throu The Lenz)方式と呼び、レンズに拠らず誤差の少ない測光方式のため１眼レフカメラの殆どに採用されている。センサーをミラーに仕込んだり、結像面の反射光を捉えたり、受光素子そのもので構成されている。

　中心測光でAF（自動焦点）の場合、焦点と露出を合わせたい被写体を中心に置き、シャッターボタンを半押しすると、狙った被写体に焦点と露出が合うので、そのまま構図を決め直してから更にシャッターボタンを押せばよい。画面に特に暗い部分や、逆に明るい部分が有る場合に、被写体明度基準で撮影するために使うモードである。

　平均測光では、画面全体の照度で撮影データを決める。撮影測光に特別な操作はないが、画像に特に明るいところが有ったり、全体が一様に暗い、あるいは明るい色彩だと適切な露出にはならない。

　高輝度撮影のオシロスコープ撮影では、現在はデジタルオシロが主流で、波形写真は画像データで得られるから写真撮影技術は無用である。
　しかしまだ残るCRTオシロスコープの場合は、波形トレースと画面スケールのみが発光しているのでオシロ撮影アダプターを用いてスポット露出計を用いてもまだ細線発光に適合できず適正露出が得られない典型的な高輝度被写体撮影である。オシロスコープ写真が必要な実習課題もあるのに殆どが過剰露出でまともな撮影ができてないのだ。
　この場合、あらかじめ室内光照度を基準にしてオシロ画面を設定・観測して、画面スケールの照明を決め、その画像を撮影できる撮影データ（LV値）のうち、画面の繰り返し速度から最低３トレースを目途にシャッタースピードを決め、それに合わせて絞り値を決めればよい。シンクロスコープ（トリガー掃引式オシロスコープ）ではホールドオフ時間（トリガ掃引不感時間）が意外に大きく、その分を充分加えることが必要だ。参考例:→オシロスコープ写真（アダプターなし手持ち撮影）

　この撮影データで、オシロ撮影アダプターを装着して写真撮影すると、波形トレースと目盛板に露出が合った良い写真が撮れる。写真屋に引き延ばしに出しても「波形写真基準露出だ」と指定しておけば画面平均照度ではなくきちんと印画されて返ってきた。（中学時代には学校の暗室を使えたのに高校、大学には一般に開放された暗室がなかったのだ。フィルム現像ポットだけだから、ネガを見て焼き付け発注となる。更に文書に写真を取り込むには写真用の網掛けを貼ったり、製版屋に頼んで網掛け写真にして貼ったりと、手間と金が必要だった。網掛け処理は１枚数百円〜Ａ４版で２千数百円掛かっていた。その点画像ファイルで得られるデジカメは実に便利だ。）

　この方法は仲間と高校のクラブの予算獲得プレゼンに多用し、特に注目された試作装置はレポート付きで学校に買い上げて貰って活動費を増やしたりした。内容が重要なのは当然だが、プレゼン作戦と、資料も有用である。
　露出時間の制限はCRT-TV画面撮影にもそのまま適用できる。日本標準のNTSC方式であれば垂直走査発振周波数60Hzで２本毎の飛び越し走査をしていて毎秒30枚の絵を表示しているので、最低２枚重ねで撮影するには1/15秒露出、３枚重ねで1/10〜1/8秒露出となる。[参照写真→#Sh末尾1/60秒p6177.jpg］。（液晶ディスプレーは表示応答が遅いためもっと早いシャッターでも撮影できる。
　レーダー画面など１周表示に数秒〜数10秒のものも必要数の露光が得られる時間だけシャッターを開放するが、ほとんどのコンパクト・デジカメにはバルブＢやタイムＴが無いから、１秒を越える露出の場合は銀塩カメラの出番になる。デジタル一眼にはマニアルで〜30秒・バルブがあるが）

　同じく高輝度撮影でも相対法の相手となる被写体が得られない太陽や月の場合は、その照らす照度と見かけの直径角度から輝度を求め、照度換算で露出データを概ね正確に推算できるが、雲や大気の影響による減光をその場では算出できず、露出計指示の差で補正するしかないが、内臓露出計はLV値としては表示しないので活用が難しい。晴天時の推定露出はよく適合するので、自然減光がある場合は推定露出を数段＋−加減した撮影もしておき適正露出以外を後で消去する方が手っ取り早い。
　撮影実験では快晴晴天下で感度ISO/ASA/JIS-100換算で太陽表面が33LV、満月が13LV、半月が12LV程度であり、文献ではさらに五日月で11LV三日月が9LV程度となっている。感度ISO-800だと、8倍＝23の感度だから,さらに+3LV絞ったり高速化することができる。月表面照度は自己発光ではなく太陽光の反射だから入射角が大きくなるとcosθで暗くなるわけだ。
　　　　See→・月の撮影、 ・太陽の撮影、 ・太陽＋金星の撮影
　なお、太陽表面のLV値推定計算は「平均露光」で行っており、表面輝度より輝く紅焔などを撮るには適切だが、表面を高輝度部分と考えて黒点を撮影したいとなると、平均ではない分2LV前後は開いた方が自然な写真になるわけで、何を撮りたいかで推定露光平均値から増減させることが必要である。
　　　　　　　　　　　　　　　　　　 「高輝度露出：太陽＆月」2012/08/09追記

CRT-TV画面によるシャッター速度の測定　　　<S>

シャッター速度計測
KONICA MINOLTA α Sweet DIGITAL　　#97513353
No. 1/T
(公称) 		計測値 備考
走査線
[本] 		1/T 誤差
％
p6165 4000 4.5 3500 14.3
p6166 3200 5.0 3150 1.6
p6167 2500 6.0 2625 -4.8
p6168 2500 6.0 2625 -4.8
p6169 2000 垂直帰線、計測不能
p6170 2000 7.0 2250 -11.1
p6171 1000 14.5 1086 -7.9
p6172 500 28.0 563 -11.1
p6173 250 64.1 246 1.8 51+525/2*0.05
p6174 250 65.1 242 3.4 21+31+525/2*0.05
p6175 250 53.0 297 -15.9
p6176 125 102.0 154 -19.0
p6177 60 256.0 62 -2.5 525/2-6.5
p6178 60 250.0 63 -4.8 525/2-12.5
p6179 30 判別不能
※1 525 はNTSC方式１フレーム当たりの(水平)走査線数
※2 +525/2 は飛び越し走査1/2フレーム中の走査線数
※3 +525/2*0.05 は垂直帰線期間中の走査線数
※4 30フレーム/秒∴30×525＝15,750 本/秒の走査速度
　　(原DATA写真は下記,'10/01/20撮影)
　1/60秒〜1/30秒より高速のシャッター速度は、CRT-TV画面を撮影してその走査線本数を数えることで計測可能である。TV放送を受信してその画面のコントラストを最小に、輝度を最大に設定した上で計測するシャッター速度を選んで撮影し、CRT蛍光体の残光部を除外して輝点の軌跡だけを読み出す。TV放送を受信しないと時間標準が得られずタイミングがかなり長くなるため測定の意味が無くなる。先幕-後幕式のフォーカルプレーンシャッターの場合は高速シャッターになるに従い斜めの帯になるが、幕境界に合わせた垂直線上にある走査線本数を数えれば1/15,750秒単位で計測可能である。縦置き撮影も可。
　デジタルカメラでも近年は撮像素子が高速化されていて、銀塩カメラと変わらずに計測可能である。（縦走りフォーカルプレーンシャッターのデジタル１眼レフカメラなので横置きで可
　下の計測例ではコントラストを落とさず撮影している。安いCRT-TVでは表に調整つまみが無かった。また液晶画面では応答が遅く残像も多くて全く計測不能）

　日米標準のNTSC方式TVでは、走査線１本が1/15750秒毎の繰り返しで、画面に現れない水平帰線期間がその5%、１画面の走査線数は525本だが、そのうちの垂直帰線期間が5%で、２倍の飛び越し走査をしている（＝１本置きに発光する）。この帰線期間が計測不能の誤差分になるが、繰り返しの計測で始点と終点の見える絵が得られれば正確な値を求めることができる。
　　［高速：本数N］(1/T)＝15,750／{N＋0.95･(L1＋L2)/W} [1/s]
　　　　走査線16本丁度が映っていれば約1/984秒、
　　［中速：縦幅］(1/T)＝60／{0.95･(V1＋V2)/H} [1/s]
　　　　走査線縦幅が25%映っていれば1/T＝60/(0.95×0.25)＝252、約1/252秒となる。
　　相互に先の走査線の中間に走査線を描く２倍の飛び越し走査の様子を画像から見分けることが出来て、後半の走査が判別できれば
　　［中速：縦幅］(1/T)＝60／{1＋0.95･(V1＋V2)/H} [1/s]
　後半の走査線縦幅が25%映っていれば1/T＝60/(1＋0.95×0.25)＝48、約1/48秒となるが、読み取れなかったり誤計測し易く1/60秒以上の高速側計測に留めた方が安全。
　走査線の横方向に見られる走査線幅程度の細かい点が撮影されるが、それは画像に重畳するNTSCカラー副搬送波で、１フレーム毎に逆極性で打ち消されるため肉眼では残像により見えない。
<Sh>
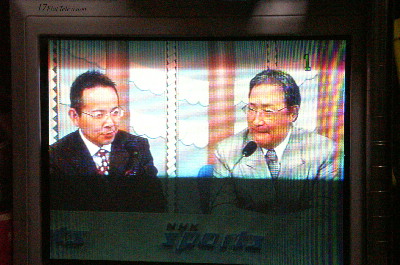1/125s
1/125s　p6176.jpg　　(一覧表の原DATA'10/01/20撮影)
シャッター速度計測画面 		1/4000s
1/4000s　p6165.jpg 		1/2000s
1/2000　p6170.jpg 		1/1000s
1/1000s　p6171.jpg
1/500s
1/500s　p6172.jpg 		1/250s
1/250s　p6174.jpg 		1/60s
1/60s　p6177.jpg
（写真をクリックすると原画表示、更にクリックすると拡大表示される）
　現用カメラでの実測例を表に示す。許容露出誤差を±1/2目盛＝１／√２〜√２と考えるときシャッター速度誤差が±20%に収まっていて、計測不能も発光しない垂直帰線期間を撮影した１枚と、判別できない1/30秒のみなのは、計測法として概ね適切で、カメラとしてもほぼ許容できる誤差範囲ということになる。概ね1/1000秒より高速シャッター領域は撮影される走査線本数が数本と少なくなるので暗い部分のない画面で計測し画面幅と輝線長の比率を読み取ることが必要になる。

焦点距離と結像位置
　　(1/f)＝(1/a)＋(1/b)　　　 <F_AB>

レンズ像 　　
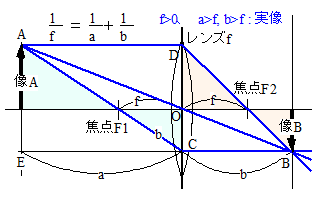
f:焦点距離
a:被写体距離 Ha：被写体高さ
b:像距離 Hb：像高さ
ルーペ像
　被写体距離ａ、像距離ｂ、焦点距離ｆの間の関係式はａ，ｂ＞ｆ：実像の場合、
　　(1/f)＝(1/a)＋(1/b) となる。
この関係式の作図での証明は(See→図上側)
  1. 中心軸を想定して
  2. レンズ中心を通る光は直進する
  3. 中心軸に並行にレンズに入射した光は焦点Fを通る
  4. 焦点Fを通ってレンズに入射した光は中心軸に並行になる
という原則で被写体と像を作図すると算出できる．
　図において、軸とEB、ADは平行線、
（色違い）２組の相似３角形の相似比より
　Hb／Ha＝f／(a−f)＝(b−f)／f
　f2＝(a−f)(b−f)
 　→　(1/f)＝(1/a)＋(1/b)　となる。

ａ＜ｆ （又は ｂ＜ｆ） ： 虚像の場合、左図下側で
Hb/Ha＝b/a＝f/(f−a) だから、
a･f＝b(f−a)
(1/b)＝(1/a)−(1/f)　………/(f･a･b)
(1/f)＝(1/a)−(1/b)
b→(−b)
(1/f)＝(1/a)＋(1/b)
　となって虚像位置bに負を割り当てると実像と同一式になる。

［接写レンズ］　　 <CU.Lenz>

　カメラの最短焦点位置より接近した写真を撮る場合には、フィルター様の凸レンズ＝接写レンズが手軽である。凸レンズの焦点距離にある被写体が、見かけ上無限遠に見えることを利用して、各カメラの最短焦点距離が無限遠焦点∞となるよう、焦点距離 1ｍ＝CU-1、1/2ｍ＝CU-2、1/3ｍ＝CU-3、1/4ｍ＝CU-4 とした市販品がある。CUの数値は度数：ジオプトリーに一致している。CRTオシロスコープの撮影アダプターのレンズは、この接写レンズに相当し、カメラを∞焦点に設定して取り付ければ観測面にフォーカスする。

接写レンズ規格
規格
CU-n 		焦点距離 備考
(組合せ)
ｍ cm
市
販
品 		1 1/1 100
2 1/2 50
3 1/3 33.33 1＋2
4 1/4 25 1＋3
推

定 		5 1/5 20 2＋3
6 1/6 16.67 2＋3＋(1)
7 1/7 14.29 2＋3＋(2)
●CU-n数は度数［ジオプトリー］
●焦点距離は1／度数[m]
●合成度数は、加算すればよい
●カメラの焦点調整分は、
　最短値を度数換算して加算する
Extention Ling
接写リング(延長チューブ)
撮像素子(フィルム面)側を延長
して最短合焦距離を短縮する
　CU-1とCU-2を同時に使うとCU-3と等価になるので、最短焦点1mほどのファインダー式カメラではCU-1とCU-2とがあれば、CU-3は代用できる。
　　　組合せ度数は、それぞれの度数を加算すればよく、
　　　度数の逆数が焦点距離［ｍ］となる。
　ほとんどの1眼レフカメラは1/2ｍまでは寄れるので実用的にはCU-1が無用で、CU-3（CU-4〜CU-2）を使う。
　　　 1/f3＝1/f1＋1/f2、 ≡　G3＝G1＋G2 →　f3＝1／(1/f1＋1/f2) だから
　　　CU-1＋CU-2＝CU-3　［∵　1/(1＋1/1/2)＝1/3m、∴CU-3 ］
　残る組合せを算出すると
　　　CU-1＋CU-3＝CU-4　［∵　1/(1＋1/1/3)＝1/4m、∴CU-4 ］
　　　CU-2＋CU-3＝CU-5　［∵　1/(1/1/2＋1/1/3)＝1/5m、∴CU-5 ］となる。
　カメラ自体の焦点機能も利用すると、それ自体が CU-1（1ｍ）〜CU-2（0.5ｍ）相当なので、上記組合せが適用される。CU-3 との組み合わせでは、CU-3〜CU-5：33.3cm〜20cmに焦点が合うが、50cm〜33.3cm（CU-2〜CU-3）は合わない。（実用上は支障ないが、）CU-2と組み合わせればCU-4：25cmまで焦点が合い、撮影可能域が連続するし、CU-3レンズ装着でCU-5：20cm相当まで焦点が合う。
　アマチュアなら資料撮影用にCU-3〜CU-4を1枚持っていれば、まず足りるが、カメラ・レンズの口径毎に準備するか、小口径を大口径側に変換するアダプター（ステップアップリング：安価）を準備しなければならない。
　以上の考え方は、望遠レンズにも広角レンズにも適用できて接写撮影可能である。但し、広角レンズでは画像の四隅が蹴られることがある。接写距離は1／(接写レンズ度数〜＋1/最短焦点）で、望遠・広角の差がほとんどなくなる。
　接写レンズを装着すると、自動焦点機能が働かないことがあり、その際は手動焦点で撮影する。
　　　　　　(2013/01/03追記)

［接写リング：エクステンション・チューブ］　 <Ext>

　接写のために、レンズ側に延長チューブ(Extension Tube)を装着して最短合焦距離を短縮することも可能。
この方式では、接写レンズによる劣化は避けられるが、撮影時の自動焦点・絞りなどは働かなくなり、機種によっては露光（絞りとシャッター）も手動モードのみになるが、寸法次第で10円硬貨を画面一杯に撮るなど超マクロ撮影が安価な機材でできる。
　右上写真のＯＭ−１／２：G.ZUIKO AUTO-S 1:1.2 F=55mm の例で動作を試算すると、
　　　レンズ：f1.2、F=55mm、最短合焦距離ａ=450mm
　　　接写チューブ：L=14mm　とあるので、計算手順としては、焦点距離と前後像位置の関係(F_AB)から最短合焦距離aでの像位置bを計算し、これに接写チューブ長Lを加えた位置b+Lに像を結ぶ新たな最短合焦距離cを逆算すればよい。すなわち、
　　　1/a＋1/b＝1/F より、b＝1/(1/55−1/450)＝62.6582、∴b+L＝76.6582
　　　　　　　　　　　　　c＝1/(1/55−1/76.6582)＝194.6697mm が新たな最短合焦距離cとなる。
　　　元々のマクロ倍率は62.6582/450＝13.92%
　　　接写チューブマクロ倍率は76.6582/194.6697＝39.4%
　　　従って14mm接写チューブ装着により撮像面には元の2.83倍(＝39.4/13.92)の大きさの画像を得ていることになる。
[実例]See→
　　αマウント：SONY、コニカミノルタαsweet用接写リング
　　各社カメラ用接写リング/Amazon
　　　　　　(2013/05/24追記)

［ルーペの倍率］　　　 <loupe>

　ルーペの倍率ｍは、虚像b を「明視の距離」≒25cmの位置に作る前提で 倍率m＝b/a として定義する。すなわち
　　m＝b/a＝f/(f−a)
　一方、(1/a)＝(1/f)＋(1/b) であるから、上式に代入すると
　∴ｍ＝f/{f−1/(1/f＋1/b)}＝1/{1−b/(b＋f)}＝(b＋f)/f＝b/f＋1＝L/f＋1
従って、(明視の距離／焦点距離)＋１ がルーペの倍率だが、明視の距離は25cmを標準とするが、人によって違い、物理量としては曖昧なため、敢えて倍率表示をせず、ジオプトリー(焦点距離ｍの逆数：下記項)や焦点距離 f のみで表す製品もある。

［ 老眼鏡の度数測定 ］　　　<glass>

　光源とスクリーンの間に凸レンズを置き、スクリーンに像を結んだ場合、レンズから光源まで、スクリーンまでの距離をそれぞれａ、ｂ［ｍ］とすれば度数Ｄは
　　　Ｄ＝(1/a)+(1/b)＝(1/f) ［度＝ジオプトリー＝１／ｍ］　　として計測できる。
　軽度遠視の１度は焦点距離で１ｍだから光源とスクリーンの距離が最低４ｍ:実際は焦点距離の５倍余が必要になり、計測設営に困難を加えるが、２度〜４度は焦点距離で0.5m〜0.25mなので最低2.5ｍ〜1.5ｍだからスケールさえあれば手軽に計測可能である。光源寄り、スクリーン寄りの２箇所で結像するので、両方を測定して誤差・誤計測に備える。
　太陽の像を結ばせる方式ならちょうど焦点距離に像を結ぶので、そのメートル単位の逆数が［度＝ジオプトリー］である。
老眼鏡
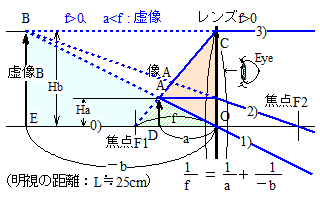
被計測老眼鏡 		焦点計測設営
焦点計測場、スクリーンと5.5m巻尺と光源
レンズ 光源像
　　　被計測レンズと巻尺　　　　　　　　　　フィラメント像
フィラメントのコイルが識別できる様な正確な焦点調整が必要 		焦点計測
焦点計測状況（結像位置測定）
右から光源、レンズ、光源像

［眼鏡：焦点補正計算］　　　 <glass-cal>

[近視補正]
●遠点距離a→∞
　1/f＝−1/a （度：ジオプトリー。以下[ｍ]単位で計算）
　［例］ 遠点距離0.80mの場合、1/f＝−1.25度
　　　　 遠点距離0.33mの場合、1/f＝−3.0 度
●近点距離a→明視の距離L　（a＜L）
　1/f＝1/L−1/a　（度：凹レンズ：a＜L）
　［例］ 近点距離0.167mの場合で、0.20ｍの位置に見たい
　　　　1/f＝1/0.20−1/0.167＝5−6＝−1.0度
　［例］ 近点距離0.167mの場合で、0.25ｍの位置に見たい
　　　　1/f＝1/0.25−1/0.167＝4−6＝−2.0度
　［例］ 近点距離0.167mの場合で、0.50ｍの位置に見たい
　　　　1/f＝1/0.50−1/0.167＝2−6＝−4.0度

[遠視補正]
●（a＞L、軽度の遠視の場合）遠点距離a→明視距離L
　1/f＝1/L−1/a　（凸レンズ：a＞L）
　［例］ 遠点距離0.80mの場合で、0.50ｍの位置に見たい
　　　　1/f＝1/0.50−1/0.80＝2−1.25＝＋0.75度(133cm)
●（a≧∞、重度の遠視の場合）焦点を結べず→明視距離L
　1/f＝1/fs＋1/L−1/a'　（凸レンズ：a＞L）
焦点を結べる補助レンズfsを介して適正fを求める。
　1/a'＋1/b＝1/fs＋1/Fe ･･････････････(1')
　1/L＋1/b＝1/fs＋1/f'＋1/Fe ･････････(2')
(2')−(1')
　1/f'＝1/L−1/a
　1/f＝1/fs＋1/f'＝1/fs＋1/L−1/a' ････(4)
　［例］ 強度の遠視で焦点の合った像を結べない場合に、補助レンズfsを装着して最適補正値を求める。
　　　その際の遠点距離0.80mの場合で、0.40ｍの位置に見たい。 補助レンズの度数は２度（焦点距離50cm)→(4)式より
　　　　1/f＝2＋1/0.40−1/0.80＝3.25度(31cm)
※ 眼には焦点調整機能があり「見易さ」で調整する必要があり、計算数値との微妙な差異を生ずる点は要注意。

［ケプラー式望遠鏡］　　　 <telescope>

　対物レンズと接眼レンズがともに凸レンズの望遠鏡を「ケプラー式望遠鏡」という。
その倍率ｍは観測対象を見込む角の比で定義する。すなわち
　ｍ＝Θ1／Θ2＝tan Θ1／tan Θ2＝b1／a2≒F1／F2

[ニュートン式反射望遠鏡]　　　 <newton>

　ケプラー式望遠鏡の対物レンズに代えて凹面鏡を用い、接眼レンズ手前に直角反射鏡を置いて鏡筒の横から観測する構造の望遠鏡を「ニュートン式反射望遠鏡」という。反射鏡には色収差がないのでレンズ式（ケプラー式）より解像度が高く、また大口径レンズを作りやすい。その倍率はケプラー式望遠鏡と同じである。すなわち
　ｍ＝Θ1／Θ2≒F1／F2
See→ 使用記：日記#291-#3

［ 顕微鏡の倍率計算 ］　　　 <microscope>

　顕微鏡の倍率計算は、その具体的構造で微妙に異なる点があるが、対物レンズを交換すると鏡筒を前後させて焦点調整を行い、接眼レンズを交換しても基本的にはほとんど調整がないという構造を前提にすると、鏡筒長Ｄは対物レンズ:焦点距離ｆ1とその実像との距離として、明視の距離Ｌを25cm、接眼レンズの焦点距離ｆ2で覗いた場合の倍率ｍとして求められる。
大括弧
ｍ＝ｍ1×ｍ2
(1/ａ1)＋(1/Ｄ)＝(1/ｆ1)
ｍ2＝（Ｌ/ｆ2＋１）　より
　　ｍ1＝Ｄ/a1＝Ｄ/ｆ1−１
∴ｍ＝（Ｄ/ｆ1−１）×（Ｌ/ｆ2＋１）
　　　≒（Ｄ/ｆ1）×（Ｌ/ｆ2）　となる。

[ 撮影データから平均照度[lux]を推定
　EV値と照度と標準反射率18% ]　　　 <EV>

　標準反射板の起源は定かではないが、フィルム面測光方式を採用するのに際してコダック辺りが提唱したもので網目パターンをランダムに様々な明度で塗って平均的な反射率18%を実現したものだと思う。その辺りの古い資料が見つからない。

　LV値が撮影機材の光量設定（絞りFとシャッター速度T）なのに対し、EV値はASAフィルム感度と実照度を含んだ実光量を示す場合に用いられる。（ところが近年、LV値の意で使われるようになり、その場合は当記事冒頭部を参照。See→LV値。撮影データの起原には無関係の諸作業にかなり長期に従事した間に様子が変わってLV≠EVが崩れた経過が分からないが、EV値とLV値がかって違っていたことと、LV値が機材の絞りF2とS値の２底の対数の和のみで定義されていることは間違いない。）

　基準照度は2.4〜2.5 [Lux]、ASA100、露光１秒とするもの(K＝2.5)と、他の値(K＝2.5〜0.432：直接測光/反射光測光)のものがあり、2.5 luxは面照度、0.432 lux（＝2.4×0.18）は反射被写界照度：Film面照度か？と見られるが、適用には原定義の調査を要す。
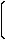
Ｅ＝２EV ＝K･ F2(1/T)／(ASA/100) [lux] （但しK：Film面基準照度、ASA感度）　が基本関係式であるから、
EV(F,T,ASA) ＝log2{K･F2(1/T)／(ASA/100)} 　
＝log2F2＋log2(1/T)−log2(ASA/100)＋log2K 　　　K＝2.5×0.18=0.45 [lux]→log20.45≒−1.15
＝log2F2＋log2(1/T)−log2(ASA/100)−1.15 　　　（Ｆ2，Ｔ，(ASA/100) 規格値は絞り開放以外はほとんど総て２n上の数列であるから対数の底は２で演算できる)
照度Ｅ ＝0.45 ･F2(1/T)／(ASA/100) [lux] ＝２EV [lux]　　 として撮影データからフィルム面照度を推定できる.
直照度は
直照度Ｅ ＝2.5 ･F2(1/T)／(ASA/100) [lux] ＝２EV/0.18 [lux]　　 として撮影データから直照度を推定できる
なお、上式右辺２項目の和 log2F2＋log2(1/T)＝LV値 であるから
EV＝LV−log2(ASA/100)−1.15
LV ＝EV＋log2(ASA/100)＋1.15　……（内蔵露出計の動作。EVは光量計測値）
　　という関係でEV≠LVのはずなのだが……（調査要）
現在の定義は　EV＝LV　で EV が常用されています。かって EV≠LV と異なっていた経緯は分かりません・

輝度と照度　　　<Int>

　照度というのは、「受光面の光束密度」でSI単位ではLux＝lm/m2であり、光源が点光源か面光源かは問わず、受光面への総光束量のみが問題となる。
　それに対して輝度は「発光面の光束密度」で、点光源であれば無限大で、面積を持てば有限の値となり、単位は照度と同じになるが、「外に対する発光」とみると、輝度は正味の発光量だが、照度は受光体の反射率（一般被写界(体)で18%？）が掛かった値が外に対して放射される点が異なる。すなわち、輝度を反射照度に換算するには、反射率で除する必要がある。逆に云えば受光面は照度×反射率の発光をしていることになる。

　具体例としては、夏季快晴日中の照度は概ね200,000.[Lux]だが、その時の太陽表面を撮影する場合、輝度は露出基準には採れず、反射と見なして太陽表面照度を仮定する必要を生ずる。
　具体的計算は、太陽撮影望遠レンズ試作「太陽表面撮影データ試算」を参照。('12/06/07追記)

照度計算：法線照度、面照度　　　<Lux>

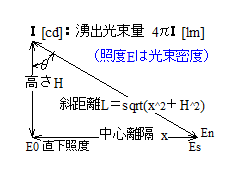
光源光度 ：I [cd] Lux計算
光源高さ ：H [m]
中心離隔 ：x [m]
直下照度 ：En(0) [lx]
法線照度 ：En(x) [lx]
面照度 ：Es(x) [lx]
面入射角 ：θ　　　とするとき、
　光源 Ｉ [cd] からの光束発散量は４πＩ [lm]で一様であるとして、その法線照度は各地点に於ける光束密度[lm/m2＝lx]である。光源からｒの位置の面積（＝球表面積）は 4πr2だから、照度E≡光束密度＝光束／面積＝4πI／4πr2＝I／r2
　従って
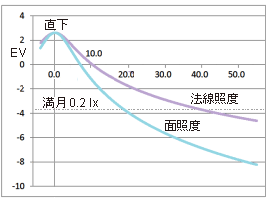
En(0) ＝I／H2 　　直下照度
En(x) ＝I／（H2＋x2） 　　法線照度
＝E0／{1＋(x/H)2} 　　　〃
Es(x) ＝En(x)･cosθ
＝I／(H2＋x2)×H／sqrt（H2＋x2）
＝I･H／（H2＋x2）3/2 　　面照度
＝E0／{1＋(x/H)2}3/2 　　　〃

[ 照明法線照度、面照度例 ］

光源高さH＝4.5 [m]、撮影データ：F＝3.5、T＝1/2、ASA＝400 の場合（実験例）
直下照度E0 ＝F2/T/(ASA/100)*2.5　………（直照度∴18%は乗じない）
＝3.52/(1/2)/(400/100)*2.5
＝15.31 [lux]
光度 I ＝E0･r2
＝15.31×4.52
＝310 [cd]　　（水銀灯50W×2相当）
従って、法線照度En(x)、面照度Es(x)は
En(x)＝I／(H2＋x2) ＝310／(4.52＋x2) ＝310／(20.25＋x2)
Es(x)＝I･H／(H2＋x2)(3/2) ＝310･4.5／(4.52＋x2)(3/2) ＝1395／(20.25＋x2)(3/2)
<照明図light.gif>
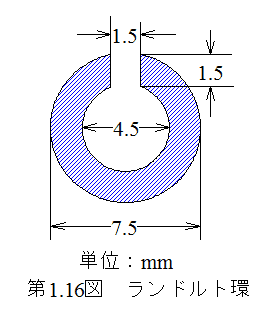<視力検査環>
外径：線幅：切欠幅＝5：1：1 が規格
　日本では上記寸法図形を5m離れて読み取れる視力を1.0とす。他の視力は反比例。距離短縮時は距離比例。

[ 照度と視力 ]　　<Lux_2>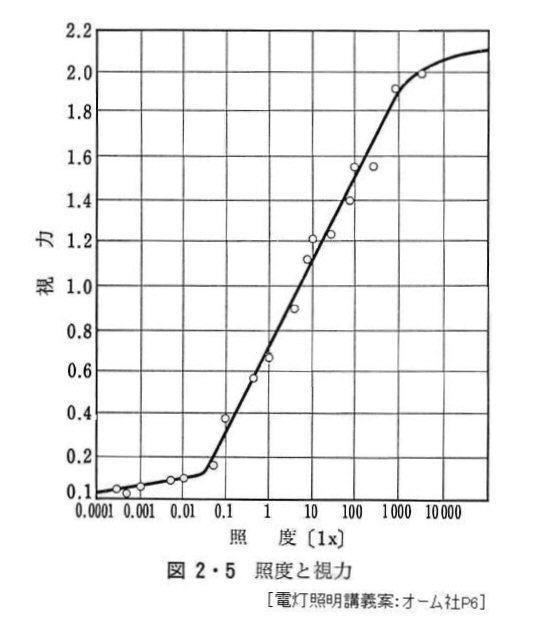

照度と視力

　高さ4.5m、310cd(水銀灯〜100W、白熱電灯100W×３)という例題の街灯は、やや明るめだが、それでも直下で15.3 lux、20m離れただけで満月の地上程度の明るさ0.2 luxにまで落ちてしまう。法線照度でみても満月照度は40mがやっと。

順応　　　　　　<Lux_3>

　目に入る光束が小さい場合、目の感度は高くなり、逆の場合は低下する。この現象を目の順応といい、明るいところへ出たときの順応を明順応、暗いところへ入ったときの順応を暗順応という。一般に、目が完全に暗順応するには30分以上の時間を要するが、明順応は１分以内で完了する。

（「照明工学」電気学会p15第1.17図、1.16図）

　こんな低照度では事件を目撃しても細かいことは分からない。夜間の「目撃情報」は思い込みで脚色されやすく慎重の上にも慎重を期さねばならない。被害者と加害者を取り違えるような誤認も少なくないのだろう。


　何度も殴る蹴るで金銭要求を繰り返していた街のダニ：与太者「先輩」に襲われて衣服も破られ思わず大声を上げながら反撃したのを、住人がその声を聞いて反撃部だけ目撃したことで攻守逆転で恐喝（強盗）被害者をあべこべに暴行傷害犯にでっち上げて半年以上勾留して有罪にするという酷い例もあった。目撃証人にその状況を確認できれば反撃部分しか見てないのは明らかになったが、裁判では検察側が病気の診断書で証人を出廷させずに証人調書を採用させ、裁判官が暴行で立件された恐喝被害者に「暴行され服を破られたのと、それに反撃して怪我を負わせたのは別の事件だ」と説示したのだとか。事件の発端である街のダニ先輩側の常習的恐喝や暴行は判決時の説示として存在を公式に指摘しながら、全くお咎めなしなのだ。

　また、誤認で家裁と高裁を何回かの差し戻しで長期に行き来して無罪で決着した調布駅南口暴行事件など、照明は複数あっても視界に輝度の高い照明があっては中高年は幻惑されて分からないのに、警察、家裁、「目撃者」が思い込みで無実の少年達を訴追、その無罪確定後も警察幹部が地域有力者を集めた様々な催しで「あれは真犯人！立証方法を間違えて無罪にされてしまった」などと宣伝する異常事態になった。調布警察は暴力団絡みの暴走族など地元の恐喝組織にはかなり甘い。

　街のダニの被害を避けるには完全絶縁が有効なのだが、そうすると子分系列から学校などでの集団いじめや、ハブリと呼ぶ村八分の対象とされ、集合住宅階段下で子分達がずっと張り込んで威圧するとか耐え難い扱いを受けるため、街で会えば挨拶せざるを得ない関係に追い込まれる。「なぜ逃げた！」とリンチに遭うからだ。大抵は友人関係丸ごとが支配下に取り込まれており、それに断固耐え闘う決意＝友人関係絶縁の覚悟ができない限り、ずっと恐喝・暴行を甘受する財布扱いにされてしまうのだが、何段階もの支配で絶縁され級友だけ取り締まられて上部支配者には追及が及ばない。こういう集団いじめと恐喝の対象にされての不登校もかなりある。

　ほんの一部でも否認している限りは半年〜１年も拘束して自白を強要！あれでは冤罪を作るだろう。調布駅南口事件は地域の土建労働組合が長期裁判の間、就職できない被告たちの無実を信じて支え、最終的に無罪・不処分となったが、生活保障と裁判費用・運動費用が得られない被告は無実を主張しきれず冤罪に沈んでしまう。三多摩、特に調布警察では酷い事件が続いた。

2009/12/24　21:30, 2003/02/11
[Page Top↑] 戻る
前