[VBA函数定義]

mail to: adrs BBS 旧 前 主目次

表計算ソフトでの
ユーザー定義函数

【 Ｌ１２３函数定義法と留意点 】

　スクリプトエディター内での式の記述法はVisual Basicそのものである．
例えば平方根は，L123内では「@sqrt(式)」であるが，函数内での記述は「Sqr(式)」となる．

• Ｌ１２３起動
  ［函数定義操作］
  
• 「作成」をクリック→プルダウン作業メニュー表示
  
• 「＠函数」をクリック→命名窓表示
  
• 函数名指定(この時名前のみ．＠や変数リストは付けない)→
  
• okをクリック→函数定義窓表示
  
• 函数名の後に「，」区切りで（）で囲んだ変数リストを付す（Visual BASIC方式の記述）
  
• 函数内容定義：函数名を変数名としてVisual BASIC代入式を定義する
  
• 記録：記録アイコンをクリック
  ［函数定義内容の変更］
• 編集→スクリプトとマクロ→スクリプトエディター表示→
  →オブジェクト→(gloval等選択)→スクリプト（函数）名選択
  
• 内容編集
  
• 記録：記録アイコンをクリック
  定義函数の利用
  
• 定義した函数をL123内で使う場合には，それぞれの函数名冒頭に「＠」を付し，変数部にセル名を記述する.
  

【 Excel函数定義法と留意点 】　　　　　　<DEFFN2>

　ＶＢＡ内での式の記述法はVisual Basicそのものである．
例えば平方根は，Excl内では「＝sqrt(式)」であるが，VBA定義函数内での記述は「Sqr(式)」となる．
　なお、Office 2007/Office 2010でのVBA、ユーザー定義関数使用は「開発」タグを表示させる設定が必要。（すなわち、Office 2007では左上「Officeボタン」をクリックし、現れたサブメニュー下段の「エクセルのオプション」ボタンをクリック、「開発タブをリボンに表示する」のチェックボックスにチェックを入れる。Office 2010ではタグを「ファイル」→「オプション」（左端下から２行目）→「リボンのユーザー設定」とたどり「メインタブ」中の「開発」のチェックボックスにチェックを入れる。開発タグはOffice 2007/Office 2010組込時には共に不表示である。さらにファイルの記録時は「マクロ有効」の拡張子「.xlsm」を選択指定する必要がある）

• Excel起動
  
• VBA有効化
  　　「開発」→「マクロのセキュリティー」→（「警告を表示して、無効化する／or有効化する」を選択）
  ［函数定義操作］
  
• 「ツール」をクリック→プルダウン作業メニュー表示
  
• 「マクロ」をクリック→プルダウン作業メニュー表示
  
• 「Visual Basic Editor」をクリックする
  
• 「標準モジュール」がない場合、「挿入」→「標準モジュール」でコードウィンドウが開く
  
• 標準モジュールに函数を記述する.　　（以下，記述例）
  　　　Function 函数名(変数リスト，，，)
  　　　　　函数名＝Ｆ(変数リスト，，，)
  　　　End Function
  '極座標−直交座標(Ｐ−Ｒ)変換　（例：準汎用函数→測量などの座標変換）
  '　　 Ｘ座標
  　　　Function PRX(R,TH)
  　　　　　PRX＝R*cos(TH)
  　　　End Function
  '　　 Ｙ座標
  　　　Function PRY(R,TH)
  　　　　　PRY＝R*sin(TH)
  　　　End Function
  ’論理式を用いる場合は，Basic内では，偽＝０，真＝−１ だが，
  Excel/L123 セル内では真＝１と逆符号になることに特に注意
  　　　'DMS→D.DD変換式　　(測量データ整理用)
  　　　Function DDD(DD,MM,SS) '(度，分，秒を別のセルに入力する．符号有効)
  　　　　　DDD＝DD+(1-2*(DD<0))*(MM/60+SS/3600) 'DD<0 で分秒の符号反転
  　　　End Function
  
  
• 記録終了：左上ファイルをクリック，プルダウンメニューの「終了してExcel に戻る」をクリック
  
  定義函数の利用
  
• 定義した函数をExcel内で使う場合には，先頭の場合のみ函数名冒頭に「＝」を付し，変数部にセル名あるいは式，定数を記述する.セル冒頭が等号「＝」の場合、セルは式である．函数名は＝を含まない。
  　＝冒頭でない場合には「＝」を付けない．付けるとERRORになる．
  　123 vs Excel：π×πの表記法
  　　　123：　@pi*@pi　　　　　それぞれの函数名の冒頭が「＠」
  　　　Excel　=pi()*pi() 　　　式項の冒頭のみ「＝」。函数名に「＝」は付かない。
  

条件判断分岐を含む函数　　If Then Else,　Do Loop until

　算出可能な逆函数の存在しない連続函数の方程式の根は「ニュートンの求根法」などの試行錯誤法をプログラム化して近似値を求めている。そのプログラムには誤差が許容範囲かどうかの条件判断部があるが、これを表計算ソフトのユーザー定義函数にも取り込めることが確認された。条件ジャンプ先はラベル指定が可能だが、プログラムの見通しの良いDO,LOOP UNTIL X による条件付き繰り返しも使用可能だった。ラベルは行頭に置いて最後に「：」を付して定義、行番号は存在せず使用不能、If,Then,Else文にはブロックIf機能があり、各ステートメントを独立行に記述するとブロックIf文となり、ジャンプ機能としては(N88BASICなど一般的BASICでは許容された「Then ラベル：」は動作せず、「Then Goto ラベル：」と記述する必要があった。以下、一般に広く使われる均等割ローン＆年金原価計算で金利を逆算する逆函数を例として示す。

<PV>

年金原価＆均等払ローン計算

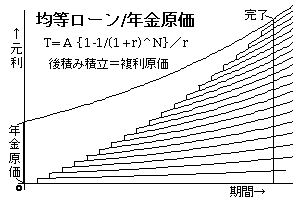　ローンや有期年金の計算は、指数函数と等比級数の和の応用として複利計算、積立預金（後積み）を組み合わせて算出され、
　借入額＝毎期返済額*{1−1/(1＋利率)^^期間}／利率
という関係になる。式導入の考え方としては「年金原価・借入額の複利元利合計と、複利積立預金の元利合計が等しくなった点で相殺処理を行う」というのが基本で、複利積立預金の元利合計は等比級数の和として算出されるが、一般の積立預金では冒頭積立なのに対し、ローン＆有期年金計算では各期末積立で最終積立と同時に冒頭の借入金あるいは年金原価と相殺処理が行われることが違い、元利合計で１期分の利息の違い×（１＋利率）ができる。（ここを見落として機械的に公式を当てはめて計算間違いを生ずることが多い）
　上記方程式では利率を未知数とする形には変形できないので、ニュートン法などの試行錯誤法で利率を逆算することになる。

ニュートンの求根法

技術評論社刊 The BASIC '92/04号 「DEF FN活用ハンドブック」p　 水島哲生執筆より引用

　ローン計算で、借入額T、毎期返済額A、返済期間N、利率r とするとき、原函数を前出式として逆函数RI(T,A,N) を定義すると

See→<Newton>の求根法

原函数
　　T(A,N,r)=A{1-1/(1+r)^N}/r　　　となる。
逆函数の定義に当たって、利率rの取りうる値域を求め、その範囲内の初近似値を求めて求根収束ループに渡す。すなわち
　　T≦A*N だから、T＞A*N では解なし、不能
　　　　　T＝A*N では　r＝0
　利率初推定は、複利で長期分割で、0≦RI₍₀₎≦A/T の中央､
　　RI₍₀₎＝A/T/2
　　　あるいは単利からの推定値
　　RI₍₀₎＝(T-A*N)/T/N、のどちらかを選ぶ。上が単純で好。
　　根推定函数は
　　　　T(r)＝A{1-1/(1+r)^N}/r−T
　　接点勾配は　α＝{T(r＋Δ)−T(r−Δ)}/２Δ
　　推定根修正値は
　　　　Ｄ＝T(r)／α
　　　　　＝Δ{T(r＋Δ)＋T(r−Δ)}
　　　　　　／ {T(r＋Δ)−T(r−Δ)}
　　RI＝RI+Ｄ が新推定値となり、
　　この修正値Ｄが許容誤差範囲に収まるまで根推定計算を繰り返す。
　以上により　RI(T,A,N) 函数、およびその原函数であるGENKA(A,N,r) 函数を定義する。

<Intr>

[函数例]　　(123/Excel共通)
Function GENKA(A, N, r) 　　　　　　　　'[年金原価：PV(A,r,N)]
　　If r = 0 Then
　　　　GENKA = A * N
　　Else
　　　　GENKA = A * (1 - 1 / (1 + r) ^ N) / r
　　End If
End Function

Function RI(T, A, N)　　　　　　　　　　'[年金利率逆算]
　　Const e = 1 / 100000　　　　　　　　　　'0.001%許容誤差&微小変位
　　If A * N = T Then
　　　　RI = 0　　　　　　　　　　　　　　　'無利息
　　Else
　　　　RI = A / T / 2　　　　　　　　　　　'仮推定初期値
　　　　Do
　　　　　　T1 = GENKA(A, N, RI + e) - T
　　　　　　T2 = GENKA(A, N, RI - e) - T
　　　　　　D = (T1 + T2) / (T2 - T1) * e　 '補正値算出
　　　　　　RI = RI + D　　　　　　　　　　 '新推定値
　　　　Loop Until e > D And D > -e　　　　 '許容誤差判定リトライ
　　End If
End Function

Function TSUMI(T, N, r) 　　　　　　　　'[期毎積立額/年金支給額：PMT()]
　　If r = 0 Then
　　　　TSUMI = T / N
　　Else
　　　　TSUMI = T / (1 - 1 / (1 + r) ^ N) * r
　　End If
End Function

Function NN(T, A, r)　　　　　　　　　　'[期数]
　　If r = 0 Then
　　　　NN = T / A
　　Else
　　　　NN = -Log(1 - T * r / A) / Log(1 + r)
　　End If
End Function


[If Then Loop]
　利率RI()函数のリトライ部の原型は以下のIf Then ループである。
ret:
　　　　　　T1 = GENKA(A, N, RI2 + e) - T
　　　　　　T2 = GENKA(A, N, RI2 - e) - T
　　　　　　D = (T1 + T2) / (T2 - T1) * e　　'補正値算出
　　　　　　RI2 = RI2 + D
　　　　If D > e Or -e > D Then GoTo ret:　　'許容誤差判定リトライ

[真理数値による定義法]
　TRUE＝-1 であることを利用すれば以下のような定義が可能。(下線部が論理式関係)

Function TSUMI(T, N, r) 　　　　　　　　'[期毎積立額/年金支給額：PMT()]
　　TSUMI = -T / N*(r = 0)-T / (1 - 1 / (1 + r) ^ N) * r * (r <> 0)
End Function

他の函数も同様に論理式の値による真理数値で定義できる

［例題］３辺長から面積を求める（ヘロンの公式）　　　 （不合理条件判断）　　 <heron>

　３辺長からその面積を求める「ヘロンの公式」を定義。３角形を構成できない辺長を与えた場合に、「Error」として止まるが、表計算で多用していた場合にはどの値の組が誤り入力か判らないので、Error表示にあまり意味がない。そこで視覚を尊重して「面積０」と定義する。今後は最後に加わる標準の組み込み函数になりそうだ。1991年頃の表計算ソフトでは全方位アークタンジェントATN2(x,y)すらもユーザー定義で雑誌記事などとして紹介されて各自が自作し登録していたが、現在は金融関連などを中心にかなり特殊なものも組み込み関数になっていて、土地測量では多用されるはずのheron(a,b,c)が未定義というのが意外なくらいである。

Function heron(a, b, c)
　　If a + b < c Or (a - b) ^ 2 > c ^ 2 Then　　　　　'３角形構成できず
　　　　heron = 0
　　Else
　　　　s = (a + b + c) / 2　　　　　　　　　　　　　　'以下２行ヘロンの公式
　　　　heron = Sqr(s * (s - a) * (s - b) * (s - c))
　　End If
End Function

［例題］モーターの加速特性　　　 （ジャンプなし条件判断）　　 <motor>

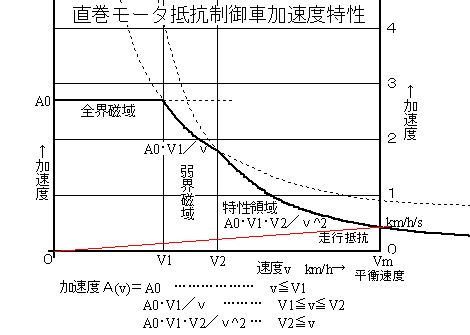
α(v)	＝α0　　………………… ＝α0・V1／ｖ　　……… ＝α0・V1・V2／v^2 ……	(　　v≦V1)… (V1≦v≦V2) (V2≦v　　)	…全界磁領域 …弱界磁領域 …特性領域

　論理数値方式でも、If Then Else 方式でも函数化可能。

Function kasoku(v,a1,v1,v2)
　　　kasoku=a1 '　　　　　　　　　　　………　v≦v1　＝全界磁
　　　If v>v1 Then kasoku=kasoku*v1/v'　……　v1≦v　＝弱界磁
　　　If v>v2 Then kasoku=kasoku*v2/v'　……　v2≦v　＝特性領域
End Function

　新幹線の基準減速度が速度ランク毎に一定値に規定されているものを、同様の区間毎定義の合成で１本の函数で定義することができる。

　尚、前出の年金原価計算
genka(A,N,r)は
@PV(投資額,利率,期間数)ソフト、毎期支払額計算
TSUMI(T,N,r)は
PMT()ソフト、利率逆算RI(T,A,N)はニュートン求根法サンプルとしてそれぞれプログラム電卓時代から添付されている機種もあって、現在では表計算ソフトの函数として毎期総支払額PMT()、元金分PPMT()、利子分IPMT()、年金原価PV(A,r,N)が既に組み込まれている。
　逆に言えば、現在未定義である利率(年金原価,期毎支払,期間)： ri(T,A,N)函数はユーザー定義函数として登録・定義するには適切な例である。度分秒を度に変換する機能は函数電卓であれば標準的に準備されている函数機能だが、パソコンには無いのでこれDDD(D,M,S)も有用だ。先の曲線速度制限公式Vrmax(R,W,C,G)もユーザー定義専門用函数にあたる。
（ Excelにはgoal seek機能やソルバー機能があって、項毎に与値変数を逆算可能だから未定義で可という考え方もできるが、一覧表作成には函数一発で総ての値が求まる方が扱いが楽だろう。)

2007/12/26　02:45最終更新　(07/12/21 12:55)

旧

前