DEF FN�������p�n���h�u�b�N
�@�@�@���l�O�v���O���}�[���c�d�e�@�e�m�����̃G�L�X�p�[�g�ɂ���@
�}�\ DEF_FNFG.pdf�֘A DEF_FN+.pdf
���M�F�����N���AThe BASIC�� 1991/02�`/05��(#93�`#96)�A�ځA�Z�p�]�_��
�@16�N�O��'90�N�Ăɏ����ꂽ�Â��L���őΏۂ�N88BASIC�ɂ͊��ɓ�������Ȃ����A�\�v�Z�\�t�g�ł������[�U�[��`�����쐬�Z�p�ɒ���������e�Ȃ̂ŁA�S����HP��up���Ă����D�iWeb.up.���M�ҏ��F�ς݁D�\�v�Z�\�t�g�p�̃��[�U�[��`�������������܂Ƃ߂悤�Ǝv���Ă���.
�@See��Excel/123�ł�VBA������`�j
�i�u���E�UFire Fox�̃����N�@�\���ꕔ���삵�Ȃ��B���̏ꍇ�̓u���E�U�h�d���g�����A������ ctrl-F�ő�p���ꂽ���BFire Fox�ł̓��x���ɏ����_�u.�v���܂ރ����N�����삵�Ȃ��B('10/08/19)�j
�c�d�e �e�m�������p�n���h�u�b�N
�@�@���l�O�v���O���}�[���c�d�e�@�e�m�����̃G�L�X�p�[�g�ɂ���@
- �y�O�z�@��
- �y�T�z ���ԂƂ���Ă����`:������Ƃ͉����I�
�@�@�@���ȏ��E�Q�l���ɂ݂颔����i���j�Ƃͣ
- �y�U�z �X�e�b�v��o�C��X�e�b�v�Ţ�����T�O�v�̊g����
- [�P] �DEF FN+�z������Œ�`�����I
- [�Q] ���E�l����ْl���`�揈���ɃJ�M
- [�R] �Ɨ��ϐ��������̔����F���Z�^�����͑��Ĕ����ł���
- [�S] �Ɨ��ϐ��������Ȃ������I�F�W���^�╶���^�����R������
- -(2) ��ʍ��W�����Ɨ��ϐ��^����
- -(3) ���W�ϊ��ɂ͓K���� DEF FN
- -(4) ��@�\�ԍ�������̣���y
- -(2) ��ʍ��W�����Ɨ��ϐ��^����
- [�T] �������������ɂ͏[������
- -(2) �{���x�u�`�k
- -(3) �{���x�b�c�a�k
- -(2) �{���x�u�`�k
- [�P] �DEF FN+�z������Œ�`�����I
- �y�V�z �����s��`���\�ɂ��� DEF FN �̑��d���i���p
- [�Q] �����������F�e�q�b�i�w�j
- [�R] ��ԥ���ٓ_�X�C�b�`�͘_������
- -(2) �_�����̒l
- -(3) ���ٓ_��ɂ����p
- -(4) ��I���A���I��
- -(2) �_�����̒l
- [�S] �L�[���͕⏕�Ƃ���DEF FN
- [�T] ��W�����I���g����
- (2) �Ƃ��Ƃ�g���L������
- (2) �Ƃ��Ƃ�g���L������
- [�U] �U�������̒�`
- [�V] �p�x�̒l��ϊ�
- [�W] �p�x�̉��Z�E���Z
- [�X] �S���ʃA�[�N�^���W�F���g
- �w,�x�Q�l���͌^�`�s�m����
- ���[�U�[��`��(DEF FN)��
- �w,�x�Q�l���͌^�`�s�m����
- [10] �E�����W/�������W
- -(2) ���E����Ⴂ�̎��v��
- -(3) �b�q�s���W�͉E(���v)���
- -(2) ���E����Ⴂ�̎��v��
- [11] ���W�ϊ��͂c�d�e�@�e�m�̓ƒd��
- [12] �x���b�ϊ���x�ϊ�
- [�Q] �����������F�e�q�b�i�w�j
- �y�W�z ���Z�͢�n��S�̂Ƃ��čl���悤
- -(2) �X�^�b�N�������[�𑝂₵�Ďg��
- -(3) ���d���p��\�肷�锟���͕�����^���Ȃ�ׂ�������
- -(2) �X�^�b�N�������[�𑝂₵�Ďg��
- �y�X�z �c�d�e�@�e�m�������p�̋�̗�
- [�P] �����@���̊��p�Ƣ���̊p�x��A����̕Ӓ���T�O�ւ̊g��
- -(1) ��ӂƈ���̒��_�p���瑼�̒��_�p
- -(2) ����̊p�x������̕Ӓ���T�O�ւ̊g��
- -(1) ��ӂƈ���̒��_�p���瑼�̒��_�p
- [�Q] ��Q�]���@���̊��p�Ƣ���̊p�x��A����̕Ӓ���T�O�ւ̊g��
- -(1) ��ӂƋ��p���瑼�̈��
- -(2) ����̊p�x������̕Ӓ���T�O�ւ̊g��
- -(3) �O�Ӓ����璸�_�p�����ށF��Q�]���藝
- -(3.b) �O�p�`�̎O�Ӓ�����ʐς����ށi�⑫�߁j
- �P�F���]���藝�A�R�����̒藝���
- �Q�F�w�����̌���
- �P�F���]���藝�A�R�����̒藝���
- -(3.b) �O�p�`�̎O�Ӓ�����ʐς����ށi�⑫�߁j
- -(4) ��Ӓ��Ƌ��p���璸�_�p������
- -(1) ��ӂƋ��p���瑼�̈��
- [�R] �g���C�A���h�G���[�@�ɂ��t�����ߎ�:
- -1). ���[��(�N������)����
�����傽���肩�̕��͂����
- -2). ���s����@�͓d�Z�@�Ɉˑ�
- -a). �j���[�g���̋����@�ł̔������p
��(��)���O �̑I��
- -b). �ӊO�ɊȒP!�������t�Z�ւ̃j���[�g�������@�̓K�p
- -a). �j���[�g���̋����@�ł̔������p
- -1). ���[��(�N������)����
- [�S] �k�b���U���g������:����Ȍ`�ł�OK!
- [�T] �g���� DEF FN����
- -a). ���l������̕�������蕥��
- -b). ���l�̗]�������w�蕶����Ŗ��߂�
- -c). �]������'0'�Ŗ��߂�
- -d). �����t��'0'�Ŗ��߂�
- -e). 16�i���̗]������'0'�Ŗ��߂�
- -f). �����ȉ��L�����w��
- -g). ���l�̏����w��ėp����
- -a). ���l������̕�������蕥��
- [�P] �����@���̊��p�Ƣ���̊p�x��A����̕Ӓ���T�O�ւ̊g��
- �y�Y�z�@��ėp�T�u���[�`����@�u�r�@��̗D��:��c�d�e�@�e�m�����
- -2). DEF FN�Ō��I�Ȍ���??
- -3). ��v�Z���̂܂܂̃I���������[�����Ó�
- -4). ���ǂ̓A���S���Y���ɋA��
- -5). ��������H�����ł́c�c�c
- -2). DEF FN�Ō��I�Ȍ���??
- �y�Z�z �킩��Ղ��c�d�e�@�e�m��`
- -2). DEF FN�G�L�X�p�[�g����l�O�v���O���}�[
- -3). �e����̐��Ƃ̕���
- -4). �c�d�e�@�e�m���K��� �U
- -2). DEF FN�G�L�X�p�[�g����l�O�v���O���}�[
- �\�T�@�P���x�����Ɣ{���x����
- �\�U�@�s�`�m(�w)�̃G���[�ƃo�O
- �\�V�@���a�̊p�x�ƍ��W
- �\�W�@�p�ی����̃A�[�N�^���W�F���g�̃I�t�Z�b�g�p
- �}�T�@�@��ӑΉ�
- �}�U�@�@�P���x�����^�ϐ��̃f�[�^�\��
- �}�V�@�@�A�[�N�^���W�F���g�Ɠ��a���W(�w,�x)
- �}�W�@�@�E(���v)�����W/��(�����v)�����W
- �}�X-a.�@�t�����̓���@�F�����@��
�}�X-b. �@�t�����̓���@�F��Q�]���@��
- �}�Y�@�@�]���@��
- �}�Z�@�@�j���[�g���̋����@
- [���X�g�T]�@�c�d�e�@�e�m������` �T���v��
- [���X�g�U]�@�j���[�g���̋����@ �T���v��
- [���X�g�V]�@�c�d�e�@�e�m�����g�p�@ �T���v��
�@�@�@�@�@�@�@�@��
�@DEF FN ������ BASIC�Ɛ��w��_�����Z�̒m�����قڂ��̂܂܊�������̂ŁA�{���Ȃ牞�p�͈͂��L���đ�ϗL�p�Ȃ͂��ł���B���ƂɃ������[�e�ʂ̏��Ȃ�BASIC�}�V���ł͌��I�Ȍ��ʂ����邱�Ƃ�����B�@������BASIC���ꎩ�̂̒n�ʂ���������������ߏ��]������Ă��錻����e�����Ă���̓I��������_�I�𖾂����܂�Ȃ��ꂸ�ɕ��u����A�v���O���}�[�X�̎��R�����ɔC�����E�l�|�ɗ��܂��Ă���B���̗ѐ���Î��ɂ��wDEF FN�������܂��g�����Ȃ���悤�ɂȂ�C�v���O���}����l�O�ł��낤�x(�BASIC�ɂ��v���O���~���O��X�^�C���u�b�N��S60�N12����\�t�g�o���N�o�ŕ�)�Ƃ����̂ł���B�w�Ԏ҂ւ̌���Ȃ̂��낤���A�^���Ƃ͏����Y��������Ǝv���B�����Ŏ��͢�A�}�m�S�U�x��ɂӂ��킵���w���l�O�v���O���}���c�d�e�@�e�m�G�L�X�p�[�g�ɂ���@�x�Ƃ��Ģ�E�l�|�̈�ʉ����ڎw���Đ������ď����A�˂邱�ƂƂ���B
�@DEF FN ���߂̓����́A�����ǂ��袔�����ł��邩��A
- ��`������́Asin,cos �Ȃnj��X�̑g���ݔ����ƑS�����������ƂȂ�B
- �f�[�^��^����ϐ����͉��ł��悭�A��`�s�Ƃ͕ʂ̂��̂��g���Ă悢�B
- ��`�s�ŁA�ʂ� DEF FN���������p���邱�Ƃ��ł���B
�@���p���� DEF FN�������ōX�ɑ���DEF FN���������p�ł���B
- �Ɨ��ϐ��̐��ɐ����͂Ȃ��B(BASIC���̂̐����ł���P�s255�o�C�g�����ƁA�������o�b�t�@�[�e�ʁA�X�^�b�N��������[�e�ʂ̐����͎�)�B
�Ƃ�������������A�v���O�������쐬����ꍇ�A
- �����𒊏ۉ����ď����̌��ʂ����悭���邱�Ƃ��ł���B
- ���Z�^�̃T�u���[�`���̂قƂ�ǂ�����DEF FN�ŕ\�����邱�Ƃ��ł�
- ���[�J���ϐ��𗘗p�ł��Ȃ�BASIC�ł��ϐ��̏Փ˂��C�ɂ������C�u�����[�Ƃ��Ďg����
- ���Z�̃����e�i���X����`���P�����ɏW�����ĊǗ����₷���Ȃ�B
- �e�L�X�g�������[�����ߖ�ł��邱�Ƃ������B
�@���̎g�����́A�l�����߂������m����z������̌`�ɐ������āA�`���ɢDEF FN���t����ƒ�`���������A���Ƃ͎g�������B�P�������ł���B�Ƃ��낪�A���̍��@�\�� DEF FN ���[���L���Ɋ��p����Ă͂��Ȃ��B�g���Ȃ������̉𖾂��܂߂�DEF FN�����̏ڍׂȎg�p�@���܂Ƃ߂悤�Ƃ��鎎�݂��{�e�ł���B
�@�a�`�r�h�b�Ƃe�n�q�s�q�`�m�̓S�L�u�����ɕK�������c��B�l�̍�Ƃ��x����c�[���Ƃ��Ă͋C�y�Ɏg���Ĉ�т��ė��肪���̂��錻���̌���ł���B���̗��p���p�ꂽ���Ƃ͈�x���Ȃ��B����̐v�v�Z�̎菇��b��Ńv���O��������Z�p�҂͂܂����Ȃ����낤�B
�@���@�P�[�V�������C�^�[�ɑ������̍�N�ċx�݂̃o�[�R�[�h�ɑ����č��N90�N�̉ċx�݂͂c�d�e�@�e�m�����œǎ҂̊F����ƍĉ�ƂȂ�B����߂ł��邪�����ď����h�ł͂Ȃ��\�t�g����h�ɂ͕K�����ɗ��̂ōŌ�܂ł��������肢�����B
�y�P�z���ԂƂ���Ă����`:
�@�@�@�@�@�@�@�@������Ƃ͉����I�
�@�����Ƃ��������͉p���function�𒆍���ɂ���Ƃ��ɓ�����'��'�Ă����ƂA���������̂ƒ����Ă��邪�A�ŋ߂̍��Z�ȉ��̋��ȏ��ł͑���'��'�Ə�����Ă���B����͊T�O�̕\�L�@�̖�肾����g�p��͂ǂ���ł��ǂ��B�I�W�����'����'����⑽�������̂����A�ᑢ�肪���D�݂̕��͌�҂�'��'��p����悢�B�@DEF FN�Ƃ͗��p�҂��l�Ă��������̃������[�R�s�[�葱���ł���B���p�҂̓��]�ɂȂ��T�O���ˑR�q�`�l���ɔ������邱�Ƃ͂Ȃ��B����DEF FN�̕�܂��锟���T�O�Ɗw�Z����Ŋe�l�Ɍ`�����ꂽ y=f(x) �Ƃ��������T�O�Ƃ��ׂ�Ƃ��Ȃ�̃Y��������悤���B���ꂪ DEF FN �̗����ƗL�����p��W���Ă���̂ł͂Ȃ����낤���B����A���c�w�r���̖{���ō��Z���ɍ������Đ��w�T�̎Q�l���F�����Ƃ���A���邠��I����60��ނ��z����Q�l������Ă���B�����Ȃ͂�������10�`20��ł��邩�碐��w�T��͍��Z�����N�ɂƂ��Ă͂��Ȃ�̋S��Ȃ̂��낤�B�Q�l���̔�����`�ɂ��Ă̋L�q��{���ƁA�S���L�ڂ̂Ȃ��܂܁A�����Ȃ�ꎟ������̐����ɂ͂�����̂����̂Q���]�Ay=f(x) �^��`���V���A�W����ꎟ�ϊ��Ǝʑ��^���c��P���Ƃ������Ƃ���ŁA�������A�����ɂ��ė�O�̂Ȃ����̂��̃Y�o���̒�`�͈���Ȃ������̂ł���B���w���Z�����N�����Ȃ蒊�ۉ����ꂽ�T�O�ł��颊��T�O��̗����Ɍ˘f���̂������͂Ȃ��Ǝv�����B
���ȏ���Q�l���ɂ݂颔���(��)�Ƃͣ
�@�܂��A�̂Ȃ�����������`�͂ǂ����������B��`�P�D�@�������i���j �^ ��`
[[�����Ƃ�]]�@��̕ϐ���,����������,���̂Ƃ�l�����܂��,����ɉ����Ă��̂Ƃ�l�����܂�Ƃ�,���͂��̔����ł���Ƃ����B
�@���̔�����\�킷�ɂ�,�ӂ��L���@��(��)�@��p����B
�@�������̔����ł��邱�Ƃ� ������(��)�ŕ\�킳���B
[�t����]�@������(��) �̕�����,�������������W�� ������(��) ���l��,
��������ɂ��ĉ����ē����邘�̔��� ������(��) ��,
���Ƃ̔��� ������(��) �̋t�����Ƃ����D
�����o��:����p���w�:�����Ȍ���ύ��Z���ȏ����쌒���Y���A���a37�N�Q��10���ѕ������s
�@���̖{�͍H�ƍ��Z�ō̗p����Ă������ȏ��ł���B���w�T�Q�l���̂قڂV�������̗�������ޒ�`�������B���݂ł͂��̒�`���P�P�Ή��ɉ��߂����̂����w�Q�N���̊w�K�Q�l���ɍ̗p����Ă���B
�������Ȃ���
- �@�Ɨ��ϐ��������̔���
- �A�l�^����
�@�����̃v���O���}�[�̔F����(�����ł͂��̌��E���z���č�Ƃ��Ă���l�ł�)��`�́H�Ƃ��܂���Ƥ���̑��������� y=f(x)�^�̉�����B
��`�Q�D�@�W����ʑ��^��`
�@�����T�O�̒�`���ŏ��ɏo�Ă���̂́A�͍̂��Z�P�N�������悤�ɋL�����Ă��邪�A���͒��w�Q�N���̐��w�ł���B�̂̒��Q�ł͎O�p��̂��Ƃ��O�p�����ƌĂъ��킵�Ă������������邾�낤���A���ۉ����������T�O�Ƃ��Ă͊w��ł��Ȃ��������ł���B���ꂪ���͒��w�R�N���ňȉ��̂悤�Ȣ���|�̒�`����s�Ȃ��Ă���B[[�����Ƃ�]]
�@�W���w����W���x�ւ̈�ӑΉ��ɂ���Ăw�̗v�f���ɂx�̗v�f�����Ή�����Ƃ�,���͂��̊��ł���Ƃ����B
[�Ή�]
�@�Q�̏W���w,�x���^�����Ă���Ƃ�,���炩�̋K��(�W)��,�W���w�̗v�f�ɏW���x�̗v�f�����т��邱�Ƃ�W���w����W���x�ւ̑Ή���Ƃ����B
[��ӑΉ�]
�@�W���w�̂��̂��̗̂v�f�ɑΉ�����W���x�̗v�f��,���ꂼ��ɂP��������Ή���W���w����W���x�ւ̈�ӑΉ���Ƃ����B
[�P�P�Ή�]
�@���̇@,�A�̐��������藧���Ă���Ή����P�P�Ή��Ƃ����B
�@�@�w�̂��̂��̗̂v�f�ɂx�̗v�f���P�����Ή����Ă���B
�A�@�x�̂ǂ̗v�f�ɂ�,�����Ή��̑���Ƃ���w�̗v�f���P��������B
�����o��:���w���w�̊�{����:�R�N:1989�����Ť�A�|�P�j���A�x�䕶��
�@����|�̒�`�����Z�̐��w�T�ł͈ȉ��̗l�ɏq�ׂ��Ă���B
��`�R.[[�����Ƃ�]]
�@�W���`�̂ǂ̗v�f�����Ƃ��Ă�,�W���a�̗v�f������������܂�Ƃ����Ή��̂��������o��:��@�ւ̃p�X�|�[�g:���w�T���쌮���Y�1986�N�����ŁA�Ȋw�U����
�@�����̃A�z���ƃh�����q�͒��R�ɂȂ�������Ƃ����āA�ʂ��Ă���Ȃ��̂𐳊m�ɗ����ł���̂��낤���H�Ƃ����ɑR����v���͂��Ă����āA
�@������(��)�^ ���̓X�}�[�g�ɢ�F���̗��j�I���W��𐋂��āADEF FN�Ɋւ��Ă����A���̋@�\���܂�����̂ƂȂ��Ă���B�������Ȃ���A���������͂��̒�`����O���B
�@���̖{�̉���ł���ӑΉ��łȂ����̂͢�����ł͂Ȃ���Ɛ�������Ă���B�������W�n�ŃO���t�ŕ\�킷�Ƒȉ~�ɂȂ锟���̏ꍇ���,���ǂ��瑤���猩�Ă��P�Q�Ή��ƂȂ�B�����炱�̒�`�ł͉~��ȉ~��`����,���̊W�͔����ł͂Ȃ��Ȃ��Ă��܂��B���������A�A�����A�Ȃǂ̊T�O��K�v�Ƃ��镪��Ƃ͈Ⴄ����(�W���_)����̃A�v���[�`������Y�����Ă���̂��낤�B������������͗����ł���̂����A��`�Ŗ��m�ɢ�Ⴄ!��Ƃ��ꂽ���̂��A��قǓˑR���̐������Ȃ������������ȂǂƂ����ďo������̂ł͑S���Ţ���w��������ʐ��Y���邱�ƂɂȂ�Ȃ����낤���B
��`�S�D �Ή��W�������H
�@�ȏ�̑S�Ă��܂ł��锟����`�͈ӊO�ȂƂ���ɋL�q����Ă����B��`�S.[[�����Ƃ�]]
�@"�������̔����ł���"�Ƃ����̂�,���̒l�ɂ��̒l���Ή����Ă��邱�Ƃł���B
�����o��:����V�̌����:S36�N�����ŁA�X�ɗY����{�r�Y������ЁD(�������̏́A��ɒl�����`�棂̉������)
�@��ӑΉ��łȂ��Ă��r�����Ă��Ȃ��̂ł���B�M�҂̐㑫�炸�ɂ�颌��藎����Ȃ̂��낤���A����Ƃ��A����ł悢�̂��낤���B
�@�Ȃ���w���{�ے��ł̢�����_��Ƃ����̂́A���f�ϕ�����ϕ��c�c�Ɛ����������Ģ�����t�c�[�̊w����ł��������ɂƂ��ėy���Y�p�̔ޕ��̍��ڂ��Ȃ��ł���̂�����Ǣ�����Ƃͣ�Ƃ����ł���{�I�Ȓ�`�͑S���L�ڂ��Ȃ������̂ł���B�܂��A���̎��ӂ͑����������n�̐l�����ł��邪�A�w�Z�𑲋Ƃ�������̎Ⴂ�l���܂߂Ĕ����̔F���� ������(��) �^�ł������B
�@���̏����I�Ȓ�`����ʏ펯�Ƃ��Ď���Ă����Ԃ� DEF FN �̔\�͂��[���Ɏg�����Ȃ��Ƃ����̂͂Ȃ��Ȃ���ςł���B����o���ɂ�鎩�R�����ɔC����邩��w�v���O���}�[�Ƃ��Ĉ�l�O�ɂȂ邾���̌o����ςƂ� DEF FN�������܂��g�����Ȃ���悤�ɂȂ��Ă���x�̂��낤�Ǝv���B����Ȃ�ADEF FN�̗��������Ȃ���A�����T�O�̊g����DEF FN�̗L���Ȏg�����������A�ǎҊe�l�̐�奌ŗL�Z�p�Ɋ�Â������������R��DEF FN�Ƃ��ă������[�ɒ蒅�����͂��ł͂Ȃ����B���Ԃ��Ă����A�q�`�l�ɒ蒅������ׂ������������Ȃ��l�ɂ�DEF FN�͎g���Ȃ��A���邢�́A���Ă鐔�w�͈͂̔͂�DEF FN���g�����Ƃ��o����Ƃ����ׂ��ł���B������DEF FN������̂ł͂Ȃ��B�{�C�Ŏ��g��œ���Ɗ�����̂ł���A����ȑO�̏����������̗̂�������ɏ�Q������̂ł͂Ȃ����낤���B
�y�Q�z�X�e�b�v��o�C��X�e�b�v��
������T�O��̊g����
�@�����T�O���̂����ۉ�����T�O�Ȃ̂����A��̗�ŔF�����L����������H�I�Ȃ̂ŏ���ǂ��ė���ςݏグ�邱�Ƃɂ���B���Ɉ��̔[������������ēx������Ƃͣ�̍���ǂݒ����Ƃ����Ɨ������[�܂邾�낤�B[�P]�@�DEF FN+�z������Œ�`�����I
�@���m����z�����̌`�ɐ������āA�`���ɢDEF FN���t�����DEF FN�̒�`�͊�������B����ȏ�ł��ȉ��ł��Ȃ��B�v���O�����Ƃ��Ă͒P������܂�Ȃ��L�q�ł���B(�z�����Ƃ����̂� ������(��)�@�̌`�ɐ�������Ă��āA���̒l�ڌv�Z�ł�����̂��w���Ă���B
�@�A�����Ƃ����̂� ��(��,��)���b�@�Ƃ����`�ŕ\�킳��Ēl�ڌv�Z�ł��Ȃ����̂�����)�B
�@�d�˂Ďw�E����A�����Ƃ����̂�sin,cos,tan,atn,sinh,log,exp�Ȃǂ̈�ʓI�Ȑ��w�����������w���̂ł͂Ȃ��_�ɓ��ɗ��ӂ��Ă��炢�����B�s�^�S���X�̒藝��A�����@���A�]���@���Ȃǂ������ꂩ�̖��m�������߂�z�����̌`�ɕϊ�����A����͂����`���� DEF FN �������ăv���O�������C���Ƃ��A��x���s���邾���ła�`�r�h�b�̑g�������ɂȂ�̂ł���B �@DEF FN���p�̊�{���͢�A���S���Y�����ǂ̗l�ȓ��e�̗z�����ɐ�������ł������I����Ƃ���(�v���O�����Z�p�ł͂Ȃ�)���ꂼ��̉��p����̌ŗL�Z�p�ɋA������̂ł���B
[�Q]�@���E�l����ْl���`�揈���ɃJ�M
�@�v���O�������L�̖��Ƃ��ẮA�ɒl����ْl��G���[�̏����ł��邪�A����͌����I�ɂ̓T�u���[�`�������ł������ł���B�A���G���[���N�������ꍇ�̍s�ԍ������������p�����s�ł͂Ȃ�DEF FN�̒�`�s�ɂȂ邤���A�ϐ��������R�Ɏg����̂ōČ������G�Ńf�o�b�O������Ȃ�̂ł���B������DEF FN���g���ꍇ�ɂ͒�`��Ƌɒl����ْl�������ɏ������ĖȖ��Ȏ��O�f�o�b�O���ς܂��Ă���g�ݍ��ނׂ��ł���B�e�X�g�ł����Ε��̓��Ăł͂Ȃ��A��ɂ�茵���Ȗ͔͉����߂��Ă��邩��A���Z�̃A���S���Y���ɂ��Ă�茵���ȗ�����v�������̂ł���B�����Ƃ����Ƃł͂Ȃ���ʂ̐l�����p����\�t�g�̏ꍇ�ɂ́A�I�y���[�^�Ƀg���u���Ώ��\�͂����҂��ׂ��ł͂Ȃ�����T�u���[�`�������ł����Ă��͔͉I��͂��v�������B���̓_�ōl�����DEF FN������Ƃ����ĉ�͂ɓ��i�̒��ӂ�v��������ł͂Ȃ��B�����͎蔲����͂̃��b�c�P�d���ɂȂ��Ă��܂����ꍇ�Ɍ�ŋN���鎖�Ԃ̉���������𑝂����x�̈Ⴂ�ł���B���̂��Ƃ́A�����܂ŁA�e���p����̌ŗL�Z�p��̖��ł���DEF FN���̂�����̂ł͂Ȃ����Ƃ͔[�����Ē����邾�낤�B[�R]�@�Ɨ��ϐ��������̔��� ���Z�^�����͑��Ĕ����ł���
�@�����`���{�a�@�c�c(�`���O)�Ƃ����Ƃ��A�`�C�a���萔�ł���Δ����Ƃ��Ă͖��_���̈ꎟ���ł��蔟���`�Ƃ��Ă�
�@������(��)���`���{�a �c(�`���O)
�ƕ\�L���Ă����B
�@�Ƃ���ł������ʌ`�Ńv���O��������ꍇ�͂ǂ����Ƃ����ƁA�w�����łȂ��`,�a���ϐ��Ƃ��Ĉ����Ēl����͂���̂ł͂Ȃ����낤���B���Ȃ킿
�@������(��,�`,�a)���`���{�a�@�@�c�c(�`���O)
�Ƃ����̂������ɍl�����ꍇ�̔����`�ł���B����͂R�̓Ɨ��ϐ����������ł���B
DEF FN���g���Ē�`�����
DEF FNF(X,A,B)=A*X+B�@�c�c(A<>0)
�ł���B
�Q�������ɂ��Ă����l�Ŏ�����
������(��,�`,�a,�b)
�@�@���`��2�{�a���{�b�@�c(�`���O)
�Ƃ����S�Ɨ��ϐ��̔����ł���B
DEF FNF2(X,A,B,C)=A*X*X+B*X+C
�Ŕ�����`�����B
�@�ʏ�̉��Z�����́A�����̓Ɨ��ϐ����Q�Ƃ��āA�ŏI���ʂ���Ƃł��邩��A�r���o�߂ꉉ�Z�������ɑg����ł��܂��Ό��Ǣ���ϐ��̔�����ɋA������B������̖��Ƃ��āA�A���S���Y�����ǂ��������Ĉ�ʉ����A�v���O�������C������₷�����āA�f�o�b�N�ƃ����e�i���X�̂��Ղ��\�t�g�ɂ��邩�Ƃ������Ƃł���B
�@�T�u���[�`�����̎������� DEF FN�����Ă��A�����̒��ۉ�:���m���̑��ɂ͂��܂���ʂ��オ��Ȃ��B�t�ɕK�R�����Ȃ��̂ɁA�S�����s�����P�{��DEF FN�ɂ܂Ƃ߂邱�Ƃ͌��ʂ���ێ琫���������ăi���Z���X�ł���B���P�ʂ̂܂Ƃ܂�̂���s�����A��ʌ`�Ƃ���DEF FN�����Ďg���ė��p���т̂ł����͂ꂽ���C�����u���C�u�����[��Ƃ��Ď��̂������I�ł��낤�B
[�S-(1)]�@�Ɨ��ϐ��������Ȃ������I�@�@�W���^�╶���^�����R������
�@������(��)�^�����g�����ꂽ�O�o�̔����̒�`���炢���A�W���^�╶���^�������ł���B�Ƃ͂�����Ɨ��ϐ��������Ȃ�������Ƃ����̂́A��ʓI�Ȑ��l�^�̔����T�O����͗����ɂ��Ȃ��R�̂���Ƃ���ł���B�����Ŏ���Ƃ��Ă`�c�R���o�[�^����̓ǂݎ����l���Ă݂悤�B�@�`�c�R���o�[�^�Ƃ͑��ʒl(�v���l)�̏W���̊e�v�f���f�W�^���l�̏W���ɕϊ����鑕�u�ł���B�f�[�^���R�}���h�̂��Ƃ�̂��߂Ƀ|�[�g�A�h���X�����蓖�Ă��Ă��邪�A����͌v���f�W�^���l�̏W���̗v�f�ł͂Ȃ��B�ϊ������͢�f�W�^���l�̏W���̗v�f���\����L�^�l�̏W���̗v�f��ɕϊ�����̂�����A�������ɓƗ��ϐ��͗v��Ȃ��̂ł���B
�@DEF FNADI=CONST*(INP(ADRS)+256*INP(ADRS+1))-CONST2
�@�@(ADRS:A/D�Ɋ����Ă�I/O�߰ı��ڽ�A�@CONST,CONST2�͕ϊ��萔)�Ƃ����B
�@������AADRS,CONST,CONST2��Ɨ��ϐ��ƍl���邱�Ƃ��\�ł���B
�@DEF FNADI(ADRS,CONST,CONST2)=(INP(ADRS)+256*INP(ADRS+1))*CONST-CONST2
�@���̏ꍇ��R�p�����^�[�����܂��Ă����ʒl�ł��锟���̒l�͓��R���܂�Ȃ��B���x���̓d���d�����̂̔푪�ʒl�̂`/�c�ϊ��o��(�v���f�W�^���l)���K�v�ł���B
[�S-(2)]�D��ʍ��W�����Ɨ��ϐ��^����
�@�b�q�s�X�N���[����̃J�[�\����X�|�b�g�̍��W���Ɨ��ϐ��������Ȃ������ł���B�m����Y���W��CSRLIN��͓Ɨ��ϐ��������Ȃ����X���W��POS()��̊��ʓ��̐��l�̓_�~�[�ʼn��ł��ǂ���������͓Ɨ��ϐ����Ȃ��B
�@N88BASIC�̃O���t�B�b�N���W�ɂ��Ă�
�@POINT(�@�\�ԍ�)
�Ƃ������������邪�A����������ɂ����ΓƗ��ϐ����Ȃ������ɕ��ނ����ׂ��ł���
�B�W���̗v�f�͊e�X�N���[�����W�ł���@�\�ԍ��ł͂Ȃ�����ł���B
�@���������g�p��͂���قnj����ɍl�����ɋ@�\�ԍ���Ɨ��ϐ��Ƃ��Ĉ����đS���x��͂Ȃ��A���ϐ��̏ꍇ�������Ɨ��_��̑��Ⴞ���ł���B
[�S-(3)]�D���W�ϊ��ɂ͓K���� DEF FN
�@CSRLIN��POS(0)��P��DEF FN�ɒu���������Ƃ���ŁA�������̕ύX�ɂ�鏈���̖��m���̈Ӗ������Ȃ����A�O���t�B�b�N��ʂƁA�e�L�X�g��ʂ̍��W�ϊ��p�Ƃ��Ē�`����ƁA���W�n��ł���̂ʼn�ʐv��������₷���Ȃ�B�����A�P���Ȕ��W�Ȃ�Εϊ��萔���`���Ă�����悸�����������`���X�}�[�g�ł���B
1110 SX%=640/80 : SY%=400/25
�Ɛ錾���Ă���
LINE(18*SX%,Y*SY%)-STEP(6*SX%,SY%)
�Ȃǂ̌`�Ŏg�p����B
[�S-(4)]�D��@�\�ԍ�������̣���y
�@POINT(�@�\�ԍ�)�����̏ꍇ�ɂͤ�������e�������I�ɂ͔���Ȃ����疼�̕ύX�ɈӋ`���o�Ă���B
���߂ɏ���������ذݍ��W(GX,GY)�����߂�͈̂ȉ��̒ʂ�ł���B
1160 DEF FNSX=POINT(2)
1170 DEF FNSY=POINT(3)
���[���h���W(TX,TY)�ł̒l��N88-BASIC�ɂ͏�������Ă���B
1130 DEF FNGX=POINT(0)
1140 DEF FNGY=POINT(1)
���ēƗ��ϐ��������Ȃ������ł���B�ǂ���̔�����������₷�����p���ł̊ԈႢ�����Ȃ����͈�ڗđR�ł���B
[�T]�@�������������ɂ͏[�����ӂ��I
| �w �� �b�c�a�k(�w) | �w �� �b�c�a�k(�w) | |||
|---|---|---|---|---|
| 1.00!= | 1.000000000000000# | 1.50!= | 1.500000000000000# | |
| 1.01!= | 1.009999990463257# | 1.51!= | 1.509999990463257# | |
| 1.02!= | 1.019999980926514# | 1.52!= | 1.519999980926514# | |
| 1.03!= | 1.029999971389770# | 1.53!= | 1.529999971389771# | |
| 1.04!= | 1.039999961853027# | 1.54!= | 1.539999961853027# | |
| 1.05!= | 1.049999952316284# | 1.55!= | 1.549999952316284# | |
| 1.06!= | 1.059999942779541# | 1.56!= | 1.559999942779541# | |
| 1.07!= | 1.070000052452087# | 1.57!= | 1.570000052452087# | |
| 1.08!= | 1.080000042915344# | 1.58!= | 1.580000042915344# | |
| 1.09!= | 1.090000033378601# | 1.59!= | 1.590000033378601# | |
| 1.10!= | 1.100000023841858# | 1.60!= | 1.600000023841858# | |
| 1.11!= | 1.110000014305115# | 1.61!= | 1.610000014305115# | |
| 1.12!= | 1.120000004768372# | 1.62!= | 1.620000004768372# | |
| 1.13!= | 1.129999995231628# | 1.63!= | 1.629999995231628# | |
| 1.14!= | 1.139999985694885# | 1.64!= | 1.639999985694885# | |
| 1.15!= | 1.149999976158142# | 1.65!= | 1.649999976158142# | |
| 1.20!= | 1.200000047683716# | 1.70!= | 1.700000047683716# | |
| 1.30!= | 1.299999952316284# | 1.80!= | 1.799999952316284# | |
| 1.40!= | 1.399999976158142# | 1.90!= | 1.899999976158142# | |
| 1.48!= | 1.480000019073486# | 1.98!= | 1.980000019073486# | |
| 2.00!= | 2.000000000000000# | |||
PRINT CDBL(1.23) Enter
�ƑŌ����Ē��������B��ʂɂ� 1.230000019073486 �ƕ\�������B
�@�P���x�����Ɣ{���x�����̑Ή��\[�\�T]���݂�ƈꌩ�S�z�ɂȂ邭�炢���l���Ⴄ�B���̌����͂Ƃ����A�}�C�N���\�t�g�n�̂a�`�r�h�b�ŏ����������ꍇ�A�������������������_�̏��Q�i���Ȃ̂�10�i���̏����ɑ��Ă͕K���덷���Ă��邪�A�\�����[�`���Ŗ����̂S�̂T��������s�Ȃ��Ă��̌덷�������Ȃ����Ă��邽�߂ł���B�P���x�̒l��{���x�ɕϊ�����ꍇ�A�{���Ȃ�P���x���l�̖��������̌������덷�̕������ׂ������A���ꂪ�s�Ȃ��Ă��Ȃ����猅�����덷�������B����� VAL("������")�����ł��w�肷��L�����������Ȃ���Γ����ł���B
�@VAL(STR$(X)) �̒l�ׂĂ��ċC�t�����̂��������� USING "#.##�c(������15��)�c#"�ɓK�p����Ɛ������{���x�ɕϊ�����邪 X#=VAL(STR$(X)) �ł� CDBL(X) �̏ꍇ�ƕς��Ȃ��B����̊���͂����肵�Ȃ��̂����������̂��B
�@���Ȋw�v�Z�Ŋ�{�P�ʂ�����g���ꍇ��A���������Ő���������g���ꍇ�ɂ͂��̐��x���ς����Ȃ����͏�Q�ɂȂ�Ȃ��̂�����ǁA�x���b�ϊ��Ȃǂ�����ƌ덷�̉e���ɂ���ď��_���Ƃ��Ă͐������̂ɏ������ɑ傫�Ȍ덷�������邱�Ƃ�����B���̌덷���[���z�����Ĕ������\������K�v������B����� DEF FN �Ɍ��������Ƃł͂Ȃ�����G���[�̔���������̂œ��ɐT�d�Ɉ����������悢�Ƃ������Ƃł���B���̏����ł�1/50����̌덷�������Ă͖��O�ł���B
[�T-(2)]�@�{���x�u�`�k
�܂��A�{���xVAL�����́AVAL�������W���ȏ�̗L���������w�肷��Ɣ{���x�ϊ������鐫�����g���āA�������ɕ�����̃[����t�������Ă���B�A���A�����l������ɏ����_���Ȃ��ꍇ�ɂ̓[���̐��������������̂Ń[���̑O�ɏ����_��t�������Ă���B(1210�s)
[�T-(3)]�@�{���x�b�c�a�k
�@�{���xCDBL�́A�{���xVAL���������̂܂܈��p���āA���l����ɕϊ����Ă�������n���Ηǂ�(1310�s)�B�P�ɕ�����ɂ��Đ��l�ɖ߂������ł͔{���x�͕ۏႳ��Ȃ��B
1200 ' �{���xVAL �� �����_�t�� �� 0 �t��
1210 DEF FNVALU#(X$)=VAL(X$+STRING$(-(INSTR(X$,".")=0),".")+"00000000")
(�X�Ɏw���\�����[�h�ł̌듮�����s�Ȃ��ƈȉ��̃��C���ƂȂ�)
1210 DEF FNVALU#(D$)=VAL(D$+FNVALDP$(D$)+STRING$(8,"0"))
1220 DEF FNVALDP$(D$)
=STRING$(-(INSTR(D$,".")=0 OR INSTR(D$,"E-")>0),".")
1300 ' �{���xCDBL
1310 DEF FNCVDBL#(X)=FNVALU#(STR$(X))
�y�R�z�����s��`���\�ɂ���
�@�@ �c�d�e �e�m �̑��d���i���p
�@����܂ł̔�����`�ŏd�v�Ȃ��Ƃ��܂Ƃ߂Ēu�����B- �@ DEF FN �̒��ɕʂ� DEF FN�����p���邱�Ƃ��ł�
- �A �ǂ�����ɐ錾���Ă��x��Ȃ��A
- �B �����̔����͌ォ��錾���������̗p�����
- �C DEF FN�̔������ɕt����ϐ��^�錾�͗L����
�@�������͗��p���鏇���ɂ������Ȃ����ۂ̔������p�܂ł̊Ԃɐ錾����悢���A���s�r���Ŕ����̒�`���e��ύX���Ďg�p���邱�Ƃ��ł��邩�瓮������ɂ�蔟����`��ς��Ȃ��珈�����邱�Ƃ��ł���B
�@�����̌^�錾�Ŕ������Ɂ���t����Əo�͂�������ł��锟���ƂȂ�A����t����Ɖ��Z���x���オ��B
�@�܂����i���p�����������͎��p���ςȉ��l������B�������e�����Ē�`���镛��������Ԗ��ɒ�`���āA�������������`�ŖړI�̔������`���邱�Ƃɂ����DEF FN�̎��P�s�ȓ��Ƃ���������˔j���āA���Ȃ莩�R�ɔ�����`���邱�Ƃ��o���邩��ł���B�ǂ̔������������Ƃ��đ�������p�ł���̂ŁA���Ԓi�K�̕��������`���đ��i�K�ɔ������p���d�˂�X�^�b�N��������[��G���A�̋�������X�ɑ�K�͂̔������`���ė��p���邱�Ƃ��ł���B
[�Q]�@�����������F�e�q�b�i�w�j
�����������߂锟���e�q�b�i�w�j�͂g�o��e�N�g���Ȃǂ̉Ȋw�Z�p�p�R���s���[�^�ɂ͓��������Ƃ��ď�������Ă���B�����DEF FN�ō\�����悤�ƌ����̂ł��邪�A�������Z�ɕ��������_�Q�i�@��p����@��ł͑O�o�̏������Q�i�\�L�덷�ɂ�錅�����Ŏv��ʗ������ɂ͂܂��ċ�J���邱�ƂɂȂ�B�}�V�����a�b�c(�Q�i���P�O�i�@)���Z�ł���ΑS���x��Ȃ��̂����A�}�C�N���\�t�g�n�̗l�ɏ��Q�i���Z�ł͏������������Q�d�Ɉ��p���锟����`�͉�����邩�A�܂��͔����̐��x�����炩���ߌ��肵�āA�ő包�����덷�ȏ�̕�l����ɉ��Z���Č����������Ȃ���Ȃ�Ȃ��B�@���^�̂e�q�b�i�w�j��
1410 DEF FNFRC(X)=X-FIX(X)
�Ɣ�����`�����B���ꂪ���d���p�ɂ���Ăǂ̗l�Ȍ덷���N�������������Č��悤�B
X=1.30:Y=FNFRC(X)*100:
Z=FNFRC(FNFRC(X)*100):?X,Y,Z
�ƑŌ�����Ɖ�ʂɂ͈ȉ��̗l�ɕ\�������B
1.3 30 .999996
�@������ FNFRC(X) ���d�Ɉ��p����'Z'�̒l:.999996 ���܂�ł��������B�{���Ȃ�O�̔��ł���B����͂x�̒l: 30 �����ۂ� 29.999996 �ł���̂��V�X�e���̕\�����[�`�����������ۂ߂ĕ\����������ɑ��Ȃ�Ȃ��B[�\�P]�߂�Ɣ����͌������������ł���B����ł͕|���Ďg���Ȃ��B
�@PC-98�̃��[�U�[�Y�}�j���A���ɕϐ��\���̋L��[�}�U]�������āA����ɂ��Ɖ������̏�������23�r�b�g������24�r�b�g�ڂ����������邱�Ƃ����炩�Ȃ̂ŁA�������̏C���͉��Z�r���Ŕ{���x�ϊ����Ĉ����ꍇ�ɂ�24�r�b�g�ڂɉ��Z���邱�Ƃ��K�v�ł���B
�P/�Q23=1/ 8,388,608��1.1921E-07
�P/�Q24=1/16,777,216��5.9605E-08
 ���̕���s�Ȃ��Ģ��������������`����ƈȉ��̒ʂ�ł���B
���̕���s�Ȃ��Ģ��������������`����ƈȉ��̒ʂ�ł���B1410 DEF FNFRC(X)=BRW#*X-FIX(BRW#*X)
1420 BRW#=1.00000006#
�@��L�̌������C�����{����FNFRC(X)�����œ������������ƍ��x��
1.3 30 5.6147E-06
�ƕ\�������B�����10-8�䂾����덷�Ƃ��Ă͒P���x�͈̔͂ł��邪�A�x���b��p����ꍇ�A���������R���ɂȂ��0.5�b�O��̌덷���鐸�x�ł���B
[�R]�@��ԥ���ٓ_������ւ��͢�_�����X�C�b�`���
�@��Ԃɂ��L�q�������ς��ꍇ�A��Ԗ��̊e�L�q�����ɘ_������p������ԃX�C�b�`��݂��āA��ԊO�̒l��^����ƃ[���������悤�ɂ��Ă����B�����̋�ԋL�q���𑍂ĉ��Z����ƑS��`��ɂ��Ă̔������\���ł���B��`��̋�Ԃ��̔���������(��)�Ƃ���Ƃ����`��S�̂̔����Ƃ��Ă�
g(x)=g1(x)+g2(x)+g3(x)+g4(x)+�c�c
gn(x)=-fn(x)*(Xn<=x AND x
[�R-(2)]�@�_�����̒l
�@��_�����̒l��Ƃ����̂́A�_�����̓��e����U�(�������Ă��Ȃ�)�Ƃ��Ƀ[���A��^�(�������Ă���)�Ƃ��ɂ͢�|�P�v�(���邢�͋@��ɂ���Ċ�ɢ�{�P�)�ƂȂ�B�������Ԕ���̘_�������e���ɏ悸�邱�Ƃɂ���ăX�C�b�`�ƂȂ�B
�@��^��̒l����{�P��Ȃ̂���|�P��Ȃ̂��ׂ�ɂ�
�@�H�m�n�s �O Enter�@�@�@���Ƃ�
�@�H�T���S Enter
�@�H"�w"��"�`"
�ȂǂƑŌ����Ēl�ׂ�悢�B
�@�h�e���łh�e�Ƃs�g�d�m�̊ԂɋL�q�����������̔��f����_�����̒l��Ƃ��Ē�`����Ă���̂ł���B�a�`�r�h�b�ł͋t�����̢�|�P����嗬�ƂȂ��Ă���B�������A���ɂ͘_��������^��Ţ�{�P��Ȃ̂ɢ�m�n�s�@�O�����|�P��Ƃ��� Sharp PC-1350 �|�P�R���̗l�ȃ��[�U�[�������̋@�������̂ŁA�Ȗ��Ȏ��O�f�o�b�O������ɉz�������Ƃ͂Ȃ��B
�@�_�����Z�̃u�[���㐔�ł͢�P�����^�v���������A��^�����|�P��̏ꍇ�A�悸��������̐����������Ɛς̕��������]����̂ō��S�̂̋ɐ��ɂ͏[�����ӂ��K�v�ł���B���ۏケ�����_�����ɂ�鉉�Z�̃o�O�̌��ƌ����Ă悢�B�����g���ꂪ�킩���Ă��Ȃ���J��Ԃ��ԈႦ�ăo�O�`�F�b�N�Ɉ����������������ȕ����ł���B���̓_�Ɋւ��Ă�BASIC���t�@�����X��}�j���A���̢�T�v�-��_�����Z����Ţ�_�����Z�q�͉��Z�̑O�Ɉ������l��-32768����+32767�܂ł̂Q�̕␔�\���̐����ɕϊ����܂��B�c�c�c�w�肳�ꂽ�_�����Z�ł́C���̐����ɑ��ăr�b�g���Ƃɉ��Z���s�Ȃ��܂�.��Əq�ׂĂ���16�r�b�g�S����'�P'��'�^'�̏ꍇ�A�␔�\���ɂ��|�P�ƂȂ邱�Ƃ�����B�v�v�z�̖��ł���P�������ł͂Ȃ����Ƃ͐G��Ēu�������g�p�ŃG���[�̑f�ɂȂ��Ă���B
[�R-(3)]�@���ٓ_��ɂ����p
�@���̕����́A������[���ɂ�����ٓ_�ɂ����p�ł���B������[���ɂ�����͂��������ꍇ�A�G���[���N�����Ȃ��_�~�[�l��^���ĉ��Z���āA���̍�����ԃX�C�b�`�ɂ��[���ɂ��ĉe�����Ȃ�����悢�B�^�l�͓������Z���ƂĂ���ʍ��̋L�q������^������B
[�R-(4)]�@��I���A���I��
�@�召��r�I���͗ǂ����p����B�_���ɒ����ɃR�[�f�B���O����Τ�傫������I�����锟����
1520 DEF FNMAX(X,Y)=-X*(X>=Y)-Y*(X<Y)
����ό`���Ē�`�����
1510 DEF FNMAX2(X,Y)=X+(X<Y)*(X-Y)
�Ǝ�X�}�[�g�ɂȂ邪�A�������ł̌������덷�����f�����댯���l����Ǝ��͑O�҂̒�`���������B
�@���l�ɏ���������I�����锟����
1530 DEF FNMIN(X,Y)=-X*(X<=Y)-Y*(X>Y)
�����ړI�ŕ�����₷���B
[�S]�@�L�[���͕⏕�Ƃ���DEF FN
�@�a�`�r�h�b��INPUT���ͤ�J�[�\���L�[��������ƕςȃf�[�^���E������ACLR�L�[�ʼn�ʑS���������Ă��܂��ȂǁA��ʎg�p�Ҍ����\�t�g�̃f�[�^���͂�C����ɂ͂��Ȃ藊��Ȃ����݂ł���B���[�쐬�^�\�t�g�𐿂������V�X�e���n�E�X�̍ő�̢���裂��J���[�Ŕ�������ʂƁA��ʂɓ��͉\�ȂP�������̓��[�`���ł��邱�Ƃ͏��Ȃ��Ȃ��B�Ƃ����̂�����������{�I�ɂ͕\�W�v�ƂS�����Z�Ƃr�n�q�s�ł���A���ʂ��t�@�C���ɋL�^���v�����g�A�E�g���邾���̎d�l�Ȃ�A���x�̋Z�p���Z�����邱�Ƃ͂Ȃ����A�Z�p�I���e��������������Ă������ɂȂ�Ȃ�����ł���B
�@���̂P�������͎��̃`�F�b�N��DEF FN�����͗L���ɓ����B���K�����˂ė�������悤�B �@�L�[���͂P�L�[���ɓ��͂��`�F�b�N���Ĉē���x�����o����Ɠ��͂̎g������͑啝�Ɍ��シ��B�`�F�b�N���e�Ƃ��Ă͇@���l������_��A�A���t�@�x�b�g��B16�i����C���͔͈͊O��D���l+�A���t�@�x�b�g��E�V�t�g�L�[�̃Z���X�ƌ������Ƃ��낾�낤���B
1600 ' X$�������ł��邱�Ƃ̔���
1610 DEF FNNUMS(X$) ="0"<=X$ AND X$<CHR$(ASC("9")+1)
1630 ' X$�������ł��褏����_�̏ꍇ�͕t�������E$���ɏ����_�s���݂̔���
1640 DEF FNNUM(X$,E$)=FNNUMS(X$) OR X$="." AND INSTR(E$,".")=0
1700 ' X$���A���t�@�x�b�g�ł��邱�Ƃ̔���
1710 DEF FNALP(X$) =("A"<=X$ AND X$<="Z") OR ("a"<=X$ AND X$<="z")
1800 ' X$�����l���A���t�@�x�b�g�ł��锻��
1810 DEF FNALNUM(X$)=FNNUMS(X$) OR FNALP(X$)
1900 ' X$��16�i���ł��邱�Ƃ̔���
1910 DEF FNHEXA(X$)="A"<=X$ AND X$<="F" OR "a"<=X$ AND X$<="f") OR FNNUMS(X$)
2000 ' ���l���l��O�ł��邱�Ƃ̔��聩(�����̖��m��)
2010 DEF FNOUTX(X,H,L)=X>H OR L>X
2100 ' PC-9801�ż�ķ���������Ă��邱�Ƃ̔���
2110 DEF FNSHIFT=(INP(&HE8) AND &H40)=0
[�T]�@��W�����I���g����
�@[�x]�̕���������₷���Ƃ����̂͐l�ԑ��ł���}�V���̑��ł͂Ȃ�����A�}��-�}�V��-�C���^�[�t�F�C�X���ŏ�p�P�ʌn�Ɗ�{�P�ʌn�̑��ݕϊ����s�Ȃ��I�y���[�^���̗v������������B�@���̕ϊ�/�t�ϊ��͒P���Ȕ��W�ł���Εϊ��萔��ݒ肷����� DEF FN ���ێ琫���ǂ��Ȃ�B
2410 PAI#=3.141592653589793#+2.385D-16
2420 RAD#=PAI#/180#
2430 DEG#=180/PAI#
�ƒ�`���Ă�����
PRINT SIN(30*RAD#) Enter
PRINT ATN(1)*DEG# Enter �ŗǂ����礍X�� DEF FN ���`���ė��p����K�R���ɖR�����Ȃ�B
[�T-(2)]�@�Ƃ��Ƃ�g���L������
�@2410�s�̃�(PAI#)�̒�`�Ŗ����Ɏw���\���̍������Z����Ă���B����͕ϐ��������[�̂����\���ɂ͎g���Ȃ������r�b�g�܂Ő��l���`���ĉ��Z�덷�����Ȃ����悤�Ƃ�����̂ł���BN/N88-BASIC�ł͂R�r�b�g�]:��P�����\�����ꂸ���������p�Ɏg���Ă���B�Ȋw�Z�p�p�̃��[�N�X�e�[�V�����ł͕\�������{�Q���`�R�������ۂ̓������Z���Ƃ��Č������덷���ڗ����Ȃ��l�ɂ��Ă���B���̕����ɂ��z������Ƃ��̕����Z�덷�����Ȃ��ł��邱�Ƃ������B
PRINT ATN(1#)*DEG# Enter
�ɂ���Ď�������ƁA�A����Ȃ��ł� '45.00000000000001' �ł��邪��A����ɂ���Đ����� '45' ��\������B�����'���x'�̖��Ƃ��������ނ���'�C��'�̖��ł���'���i���l'�̖��ł��낤�B�Ȃ��v���O�������C���ɑS����Ō����Ă����X�g������16���\���ɂȂ�̂Ţ���X�g�������Ȃ̂ɓ��쌋�ʂ������ɈႤ��C���̈������ۂ��N�����̂�(2410�s�̗l��)���ӂ��K�v���B
�����Ă��̕ϊ�����`�����
2510 DEF FNSINDEG(X)=SIN(X*RAD#)
2520 DEF FNCOSDEG(X)=COS(X*RAD#)
�ł悢����又�����ł̊�{�P�ʍ̗p�̌����ɏƂ点�Ή��Z�����̍�������K�͂̑傫���V�X�e���قǍ̗p������������A�܂�����ł� DEF FN �ɑ���S���I���S���l����Ƃ���͕ϊ��萔�����̕��������e�i���X�S���҂��猙���Ȃ��ōς݂������B�K�R���̔����_�������Z���܂܂ꂽ�肷��ƍŒ�̕]���ɂȂ肩�˂Ȃ��̂�����BDEF FN�h���h���嗬�ł��錻�݁A����p��DEF FN���͔����悤!��Ƃ����̂� DEF FN����̐G���ׂ����e�Ȃ̂��낤�B
[�U]�@�U�������̒�`
�@�����d��ł͓��R�����Ă���t�����@�\���a�`�r�h�b�ł͎����ŎZ�o���Ȃ���Ȃ�Ȃ��B����𢋉�������@��Ȃǂ�p���ė͂Â��ŎZ�o����ꍇ�ʼn��Z���x�����ɂ���A���邢�͕W�����[�`���Ƃ��đ��p����ꍇ�ɂ� DEF FN�����ނ���}�V���R�[�h��p���ă��[�U�[�������`���������悢�B�R�[�h�̃Z�b�g��
CLEAR -INT(-VOL/16) 'VOL�̓R�[�h��
DEF SEG=�c�c�cϼݺ��ނ̾����ı��ڽ
DEF USRn(X)=�@�V�@�@�@�@�̾�ı��ڽ
BLOAD "����̧�ٖ�"�@�ł��ށB
�������A�A�Z���u�����g���ĕ��������_�̐��l���Z���s�Ȃ��̂͐����Șb���Ȃ肨�������ł���A���̔����̕ό`�Ŏ����ł���̂Ȃ��ʓI�ɂ�DEF FN�̕������p���l�������B
[�U-(2)]�@sin-1�ƁAcos-1�� �����̍쐬
�@�O�p�����̋t�����łm�W�W�a�`�r�h�b�ɏ�������Ă���̂̓A�[�N�^���W�F���g:�`�s�m(�w)�����݂̂ł��邪�A�O�p�����̑��݊W���𗘗p����A�[�N�T�C���ƃA�[�N�R�T�C���������\���ł���B(���ό`�̏ڍׂ͗�)
sin2(X)+cos2(X)=1
�@�@�@�@�@sin(X)
tan(X)=�\�\�\�\�\
�@�@�@�@�@cos(X)
��TH=sin-1(X)
�@�@=ATN(X/SQR(1-X2))
�@�@X=�}1�ŤTH=�}��/2
�@ �@TH=cos-1(X)
�@�@=ATN(SQR(1-X2)/X)
�@�@X=0��TH=�}��/2
�]����
2610 DEF FNACSIN(X)=ATN(X/SQR(1-X^2-(X^2=1)))*(X^2<>1)-SGN(X)*(X^2=1)*PAI#/2
2620 DEF FNACCOS(X)=ATN(SQR(1-X^2)/(X+(X=0)))*(X^2<>0)-(X=0)*PAI#/2
������[���ɂ���Ȃǂ̓��ٓ_�ɒ��ӂ��Ĕ�����`����A���ʂ̍���͂Ȃ��Bsinh,cosh,�Ȃǂ��ȒP�ɒ�`�\�ł���B
[�V]�@�p�x�̒l��ϊ�
�@�p�x�͂P��360�x���߂���ƌ��ɖ߂�̂����礎g�p��ʂɈ˂��Ēl�悪�قȂ�B��ʓI�ɂ́}180�x(�}��)�ł��낤���q��@��D���̍q�@�⑪�ʂł͖k���O�Ƃ��Ď��v��]��360�x����ʊp��Ƃ��č̗p���Ă���B���g�p�ł͂���������}�^��Ƣ���l�^��̑��ݕϊ����K�v�ł���B�@���ʊp(0�`2��:360�x)���}��(180�x�j�ɕϊ����锟����
2810 DEF FNPNTH(X)=X+2*PAI#*(X>PAI#)
�@�t�ɤ�}����ʊp�ɕϊ����锟����
2830 DEF FNDRC(X)=X-2*PAI#*(X<0) �ł���B
[�W]�@�p�x�̉��Z�E���Z
�@�����̒l�悪���肳���Ɗp�x�̉��Z�A���Z�Ɉ˂��Đ������O�l��������Z����Z�������K�v�ł���B�@�pA,B�̒l�����ʊp(0�`2��:360�x�j�Ƃ�����Z�ƌ��Z�ͤ
2910 DEF FNADDTH(A,B)=A+B+2*PAI#*(A+B>2*PAI#)
2920 DEF FNSUBTH(A,B)=A-B-2*PAI#*(A<B)
�ƒ�`�ł���B
�@�l��̕ϊ��͑O�o�̒l��ϊ����������p���邱�Ƃ��ł��邪�A�ǂ���̒l�����Ƃ��Ĉ������ɂ�褁}�̒l��Œ��ڎZ�o����p�x�����Z�������]�܂����ꍇ������B���̏ꍇ�̔�����
XXXX DEF FNADDTH(A,B)=A+B+2*PAI#*(A+B>PAI#)
XXXX DEF FNSUBTH(A,B)=A-B-2*PAI#*(B-A>PAI#)
�ƂȂ�B
[�X]�@�S���ʃA�[�N�^���W�F���g
�@��S���ʃA�[�N�^���W�F���g��Ƃ����̂͂ǂ����낤�B�^���W�F���g�����́}90[�x]�ɕs�A���������Ĥ180[�x]�����̔���������A�q�@�V�X�e���Ȃǂł��̋t����:�`�s�m�𗘗p���ĂP��360[�x]�̕��ʊp���Z�o���悤�Ƃ���IF THEN ELSE�̎R��ɂȂ肩�˂Ȃ��B�����DEF FN�ꔭ�ŋ��߂悤�Ƃ������X�X�������O�ȗ��ł���B(���F���̔����͌��݂ł͕\�v�Z�\�t�g123-2001�AExcel-2003��JAVA��ATAN2(x,y)�����ȂǂƂ��č̂������Ă���D���̋L�����e��1991/04���s(1990/08���q)�ł��̐�삯�ƂȂ��Ă���)
�@BASIC��TAN()�����ɒP���x�̐��l��������
�@TAN(+-1.7014118E +38)
�����߂�Ƥ���ƃG���[�����̢0��ɂȂ��Ă��܂��̂Ńo�O��Ƃ��ĕK���G���[�̌����{���x�ň������ƂƂ���(�\�U�Q��)�B
| �w | �`�s�m(�w)�� | ||||
|---|---|---|---|---|---|
| �{���x | +-1.7014118346046922D +38 | 1.570796326794897 | [RAD] | ||
| �P���x | +-1.7014117E +38 | 1.57080 | [RAD] | ||
| +-1.7014118E +38 | 0 | (�P���xATN�̃o�O)
| +-1.7014119E +38 | 0Verr | OV�װ �Ŕ͈͊O
| |
�@�ő呍������ 10[�q]=10+7[�o]
�@��������\��0.1[�o]=10-1[�o]
�Ƃ���AY/X�̍ő�l��10+8�ł��褎g�p�͈͂̐��l�ł̓G���[�ɂ͂Ȃ蓾�Ȃ����Ƃ�����B
�@�`�s�m�����̏ꍇ�A����������(180�x)�����̔����Ȃ̂łP�̓Ɨ��ϐ������(180�x)�ȉ����ȏォ�f�o���Ȃ��B�����ŁA�w�x���W�����]���铮�a�̂w����,�x������^���邱�Ƃɂ���ĂP���̊p�x�邱�Ƃɂ���B
�������Ɓ��x�^�w�ł��邩��x����(�w���O)�����ْl�ƂȂ�B���̓��ْl�̕����������Ē�`���Ō�ɍ�������悢�B
| �ی� | ���@�� | ��l | ���Z�K�p���� |
|---|---|---|---|
| �T | (X>0)*(Y>0) | 0 | -------- |
| �U | (X<0) | �� | (X<0) |
| �V | |||
| �W | (X>0)*(Y<0) | 2�� | (X>0)*(Y<0) |
- 1. �w���O �̏ꍇ
- �x���O �ł͊p�x�Ƃ͎Z�o�s�\�ł��邪�A�����𒆒f�����Ȃ����߂̃_�~�[���l�Ƃ���ERROR�ɂȂ�Ȃ���:�[����I�ԁB
- �x���O �̏ꍇ�A�Ɓ��@�^�Q
- �x���O �̏ꍇ�A�Ɓ��R�^�Q
- �x���O �ł͊p�x�Ƃ͎Z�o�s�\�ł��邪�A�����𒆒f�����Ȃ����߂̃_�~�[���l�Ƃ���ERROR�ɂȂ�Ȃ���:�[����I�ԁB
- 2. �w���O �̏ꍇ
- �x���O:��T�ی�:��= ATN(Y/X)
- �x���O:��W�ی�:��= ATN(Y/X)+2��
- �x���O:��T�ی�:��= ATN(Y/X)
- 3. �w���O �̏ꍇ:��U�`�V�ی�
- ��= ATN(Y/X)+��
- ��= ATN(Y/X)+��
| �ی� | ���� | ���ʊp | ���@�@�� | �p�x���Z ��l | ||||
|---|---|---|---|---|---|---|---|---|
| �w | �x | �x�^�w | ||||||
| ��T�ی� | �k�|�� | 0�` 90 | X>0 | Y>0 | �{ | �{0�x | ||
| (�{�x��) | �� | 90 | X=0 | �� | ------ | |||
| ��U�ی� | ���|�� | 90�`180 | X<0 | �| | �{180�x | |||
| (�|�w��) | �� | 180 | Y=0 | �O | ||||
| ��V�ی� | ��|�� | 180�`270 | Y<0 | �{ | ||||
| (�|�x��) | �� | 270 | X=0 | �� | ------ | |||
| ��W�ی� | ���|�k | 270�`360(0) | X>0 | �| | �{360�x | |||
| (�{�w��) | �k | 0 | Y=0 | �O | ------ | |||
3010 DEF FNACTN(X,Y)= FNR0(X,Y)+FNR1(X,Y)
3020 DEF FNR0(X,Y)= (0.5-(Y<0))*PAI#*(X=0)*(Y<>0) 'X=0:�}90�
3030 DEF FNR1(X,Y)=-ATN(Y/(X+(X=0)))*(X<>0)+(-(X<0)+(X>0)*(Y<0)*2)*PAI#
�@�@�@�@PAI#=3.141592653589793#+2.385D-16'�@�@�@(20��)

�@�ȏ�̃��C����ʉ߂�����ł����
PRINT FNACTN(A,B),FNACTN(X#,Y#)
:R2=FNACTN(Q1#,Q2#)
�ȂǂƎg�p���邱�Ƃ��ł���B�l����}�Ƃ���ɂ͑O�o�̒l��ϊ���������p������
�@PRINT FNPNTH(FNACTN(X,Y))
�ȂǂƂ��Ďg���悢�B

[10]�@�E�����W/�������W
�@����ʊp��̏o�Ă����Ƃ���ŁA�E�����W�ƍ������W�ɂ��ĐG��Ă����������悢���낤�B�@���w�Ŋw�ԕW���I�Ȓ������W�́{�w�����E�����,�{�x����������Ƃ��ā{�w�����p�x���_�F�O�x�Ƃ��鍶�����W�ł���B�e�������ɇT�ی�����W�ی��܂łɋ敪����Ă���B
�@���ʊp�̍��W�͖k���{�w��,�����{�x���Ƃ�,�{�w�����p�x���_:�O�x�Ƃ���E(���v)�����W�ł���A���v�������ɇT�`�W�ی��Ɗp�x����`����Ă���B����Ȃ��ƈ����ɂ��Ȃ�˘f�����A���_��̈����͉E��荶��葊�݂ɕ������x���w��Ώێ��ɂ��鋾�ΏƂ̊W�ɂ��邩��A�p�x�̉�]�����������ł��邱�Ƃ������Ă͑S�����l�Ɉ����Ă悢�B
�@�x���w�̒�����ɒu����������Ċϑ�����t���̍��W��̌��ۂɌ�����̂�����A�㐔�I�ɕ����Ƃw,�x�����Ⴆ�Ȃ��l���ӂ�������_��͂≉�Z�����͓����ł悢�B
[10-(2)]�@���E����Ⴂ�̎��v��
�@�Ƃ��낪�A���v���ƂȂ�Ƌt�����W�ł͍������B�v�����u�����Ă��̕���ŕW���I�ȉ�]�����ō쐬����Ă���̂ŁA���̓ǂݎ�肾���̑��u�ł����Z���K�v�ƂȂ邵�A���Z�������s�Ȃ��C���e���W�F���g�̂��̂͑S������グ�ɂȂ��Ă��܂����Ƃ�����B
�@���ʊW�ł̓g�����V�b�g/�Z�I�h���C�g��p���邪���̕��ʊp�ڐ���͑��ĉE���ł���B���j��(�Ȃǂƍ����ĂȂ��I�R���p�X)�̖ڐ�����������k���O�x�Ƃ���E���ڐ���ł���q�s�ɂ������đ��݂ɋ��ʂ̎ړx�������ɍ����͂Ȃ��B
[10-(3)]�@�b�q�s���W�͉E(���v)���,�ꕔ�E���I
�@�R���s���[�^��f�B�X�v���[�̉�ʂ��e�L�X�g��ʁA�O���t�B�b�N��ʂƂ��ɒ������W�Ƃ��Ă͉E(���v)�����W�ł���B�{�w�����E������ł��邱�Ƃ͐��w���W�Ɠ��������{�x�����͉������ł���A�������p�x���_�Ƃ���E�����W�ł���B���w���W�Ƃ̑Δ�ł͒����x���O�����ΏƂ̎��Ƃ�����W�n�ł���A��̕��ʊp���W���E��90�x��]���������ʂƐ���������̂ł���B
�@�Ƃ��낪�AN88-BASIC�̓O���t�B�b�N��ʂł̊p�x�̎w�肪�����ƂȂ��Ă���A���W�n�Ƃ̓��ꂪ�ۂ���Ă��Ȃ��B�p�x�̍����𐳕����ɂ���̂Ȃ�A�O���t�B�b�N���W����������{�x�����ɂ���C���M�����[�ȕϊ��������ɍ�}�ł���B�e�L�X�g��ʂ̕����ɏ������Ƃ����̂ł���ACIRCLE���̉�]�����͉E���ɓ��ꂳ���ׂ��������Ǝv���B���p�ʂł�������Ă��~�O���t�͎��v���ɕ`����Ă����̂����ʂł͂Ȃ����B�����ʂȂ̂ɏꍇ�ɂ���ĕϊ����@���قȂ�Ƃ����̂͂��������Ȃ��B
�@�ɍ��W�\������ʊp����ɂ���\�t�g�E�F�A����|����ꍇ�̓V�X�e���̊�{�v�Ƃ��āA�ǂ̕����ɉE�����W�A�������W���̗p����̂��������ɋᖡ���邱�Ƃ��K�v�ł���B
[11]�@���W�ϊ��͂c�d�e�@�e�m�̓ƒd��
�@����W�ϊ�����w����̋S�壂̗l�ł��邪�A���퐶���ł͉��̒�R���Ȃ�����W�ϊ�����s�Ȃ��Ă���B���W�ϊ��Ƃ����̂́A���_�Ɗ�̕����Ɗ���@���߂āA���̊�ɂ��\�L���Ă����ʒu(���W)���A�ʂ̌��_�Ɗ�̕����A�ړx�ŕ\�킵�������Ƃł���B�y�n�̒n���ɖ��邯���s�̐��k�P��������W�ϊ����Ģ���c�n��w�����R�q��Ƃ�����w��萼���S�q����ɂQ�q��Ƃ������Ă����s�s�炿�̐l�ȊO�͑��͍���Ȃ��B���ʂ̋ɍ��W�\���ƒ������W�\�����ӑR��̂ƂȂ��Ă����̓����b���\�����Ă����ł���B���s�s�X�͗�̊����Ȓ������W�n�ł���A��G�ی��ニ��ȂǂƓ�k������̒��������ʂ�̖��O�ňʒu�w�肷�邱�ƂɊ��炳��Ă��邩��A�����̗l�Ȗ������̊X�ɂ���Ɩ��q�ɂȂ�₷���̂ł���B�ǂ����悤���Ȃ��������s�Ƃ����̂͂����͋��Ȃ��B���̍��W�ϊ�������w����̓�⣂ɂȂ��Ă��܂��̂͐��k�̃f�L�����ނ��됔�w�̃J���L�������⋳�������̕��������ƍl����ׂ����낤�B�@���ʍ��W�̕ϊ��ōł��������颒������W�̉�]�ϊ���̔����������݂悤�B�ϊ��̍l�����Ƃ��ẮA���͢�ɍ��W�\����ւ̕ϊ�����Ĥ��]�p�������Z���Ă���Ăѕʂ̒������W�ɖ߂��Ă�����A���Z������ƁA��]�������W�n����݂��V���W�͌��̂w,�x�̒l�ƍ��W�̉�]�p�Ƃ̎O�p���������ŕ\���ł���B
�@�w���� cos�Ɓ|�� sin��
�@�x���� sin�Ɓ{�� cos��
�@�ŋ߂̋��ȏ��͢�ꎟ�ϊ��Ǝʑ���̏͂ł��̕ϊ������̂�グ�čs���g���Ď��̂悤�ɏ����\���Ă���B
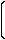 | �w |
 | �� |
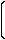 | cos��, | -sin�� |  | �~ | 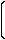 | �� | 
| �@�@�c�c�c(�s��A��p�f�\��) |
| �x | sin��, | cos�� | �� |
�@������`�͂w,�x���ꂼ��P�s���ňȉ��̒ʂ�ł���B
3210 DEF FNROTX(X,Y,TH)=X*COS(TH)-Y*SIN(TH)
3220 DEF FNROTY(X,Y,TH)=X*SIN(TH)+Y*COS(TH)
�@���̔����́A�ړ��v����덷��ŌX����̂��߂ɑ��p�����B�v�����u��ςԗ���D����q��@�Ȃǂ̉ˑ̂��X�����̊p�x�������đΒn���W�֕ϊ����邽�߂ł���B���̉�]�ϊ����ˑ̓����W�ł̐��������킹�ƁA�Βn����W�ւ̕ϊ��̂Q�i�K�Ɏg���Đ�Έʒu���Z�o���Ă�����ł��邪�A�v���O�������C���Ƃ��Ă͂P�i�K���P�s�ōς�ł��܂��B
�@�Ƃ��낪�A�̂̍��Z�̋��ȏ��ɂ͂��ꂪ�f�ڂ���ċ��Ȃ������I(���̋��ȏ��ɂ͂܂��ڂ��Ă���!���݂̍��Z�����N�ɂƂ��Ă���ͤ��낱��!�Ȃ̂�?��D���l!�Ȃ̂�?)�B���̉�]�ϊ����A�w�I��}�ɂ���ĉ�͂��e�ی�����IF THEN �ŕ������Ă��̏ꂻ�̏�ŐV���W�̒l�����߂Ă�����v���O�������C���̗ʂ͖c��Ȃ��̂ɂȂ�B����DEF FN���P���Ȃ̂̓A���S���Y�����P���Ȃ��߂ł���BDEF FN���V���v���ɂ�����ł͂Ȃ��B
[12]�@�x���b�ϊ��A�x�ϊ�
�@60�i�̓x���b��x�����̏����_�ŋ���� DDD.MMSS �ŕ\�킷�Ɠ��o�͂̎g�����肪�悢�̂ŁA�����d��ɂ͂��̕������̗p����Ă��邪�A���Q�i�@�̉��Z�ł��̕������̗p����ƁA�O�o�̌�������̂��߂Ɍv�Z���x��0.5�����ǂ����邱�Ƃ͂ł��Ȃ��B�������v����̏o�͎��̂��x���b�Ƃ����̂������̂Ŋ��Z�������������������悢�B? FNDMS#(21.5000),FNDEG#(21.2960)��Enter
�ȂǂƂ��Ďg�p����B���x��0.5���]�A10�i�@�ł� 0.00014 ���x�̂܂�߂ɂ��덷���܂܂�Ă���B
' DDD.MMSS �� DDD.DDDD �ϊ�
3510 DEF FNDEG#(X#)=FNDMI(X#)+FNDF1#(X#)+FNDF2#(X#) 'DMS$-->DEG
3520 DEF FNDMI(X) =FIX(X*BRW#):BRW#=1.00000006# '������
3530 DEF FNDF1#(X#)=FIX(FNFRC#(X#)*100)/60#
3540 DEF FNDF2#(X#)
�@�@�@�@�@�@=FIX((FNFRC#(X#)*100-FNDF1#(X#)*60)*100+SGN(X#)/2)/3600#
' DDD.DDDDDD �� DDD.MMSS �ϊ�
3610 DEF FNDMS#(X#)=FIX(X#)+FNMM#(X#)/100#+FNSS#(X#)/10000#
3620 DEF FNMM#(X#)=FIX(FNFRC#(X#)*60)
3630 DEF FNSS#(X#)=FIX((FNFRC#(X#)*60-FNMM#(X#))*60+SGN(X#)/2)
�y�S�z���Z�͢�n��S�̂Ƃ��čl���悤
�@�e��v���V�X�e���̗l�ɎZ�o�l����������āA���ꂪ�݂��Ɋ֘A���Ă���悤�ȏꍇ�A���Z�����͊�{�P�ʂƊ�{��ɂ���čs�Ȃ������V���v���Ńo�O���������ɂ����Ȃ�B���p����Z�o���ɕϊ��萔��������A�e�l�����Z�Ɉ��p���閈�ɕϊ��萔���悸��̂͌����ăX�}�[�g�ł͂Ȃ����肩�o�O�����̉����ɂȂ肩�˂Ȃ��B���������X�̕ϊ��� DEF FN��p���邱�Ƃ͂ł��邪����͊��҂ł��Ȃ��B���G�ȉ��Z�����͢�l�j�r�`�L���P�ʌn��Ȃǂ̊�{�P�ʌn��p���āA�p�x�̒P�ʂ�BASIC�ł̊�{�P�ʂł�����[rad]�ɓ��ꂵ�ėp���������V���v���ɂȂ�B��L���P�ʣ�Ƃ����̂͌��ۂ���Ԃ̗��̊p:�S��[��ޱ�]�Ŋ������P�ʌn���w���Ă���B�e���`���ɂ₽��ƂS���o������B
�@�ł́A�ǂ�ȏꍇ����{�P�ʗD�悩�Ƃ����Ƃ����ł͂Ȃ��B�V�X�e���Ƃ��Ď��p�P�ʌn�ő���(�O�p�������قƂ�ǎg�킸��)�������Ă��āA��v���ŕϊ��̕K�v���S���Ȃ��ꍇ�Ɋ����Ċ�{�P�ʂɕϊ����t�ϊ�����K�v�͂Ȃ��B
�@DEF FN�͉��Z�̎啔�ɓK�p���������L���Ȃ��Ƃ������BDEF FN������ꍇ�ɂ̓A���S���Y�����V�r�A�ɋl�߂�K�v����A��荇���I�ȃA���S���Y��������ꍇ������A�X�ɃX�}�[�g�ɂȂ�B
[�S-(2)]�@�X�^�b�N�������[�𑝂₵�Ďg��
�@FOR NEXT,WHILE,DEF FN ��T�u���[�`�����g���ƃ��[�U�[��X�^�b�N��������[���g����B���G��DEF FN �ł̓X�^�b�N��G���A���g���s������ Out of memory error ���ł邱�Ƃ�����B�X�^�b�N�̈�̑傫���� CLEAR���Ŏw�肷�邱�Ƃ��ł���B�l�r�|�c�n�r�łm�W�W�|�a�`�r�h�b�ł� CLEAR���̑�Q�p�����^�[��m�d�b�@�Y�t�̂m�W�W�|�a�`�r�h�b�i�W�U�j�ł͑�R�p�����^�[���X�^�b�N�������[�e�ʂ��w�肷��B�m�ۂ����e�ʂ͗^�����p�����^�[��16�{�ł���B���w��̏ꍇ�̃f�t�H���g�l��&H20�ŁA���̗e�ʂ�&H200��512�o�C�g�ł���B
�@�A���A�X�^�b�N�̈�𑝂₷�Ƃ��̕��e�L�X�g�G���A���������邩��A�e�L�X�g�G���A�̋�e��:FRE(1)�̒l�ɒ��ӂ������̌��ˍ������l���Ċg������K�v������B
[�S-(3)]�@���d���p��\�肷�锟���͕�����^���Ȃ�ׂ�������
�@������Ɋւ���DEF FN�𑽏d�Ɏg���Ƃ��Ȃ�p�ɂ�
�@�@string fomuiar is too complex
�Ƃ��� error����������B���̏ꍇ�A�����̍\����S���ς��Ȃ��Ǝg���Ȃ����Ƃ������B������A���d���p���\�肳���ꍇ�͕������^�����d�Ɉ��p�����̂��Ȃ�ׂ�������K�v������B�P�ƂŃf�o�b�O���鎞�ɂ͐��m�ɓ����̂ɑ��d���p�ł͑S�������Ȃ��Ȃ�̂�����n������邢�B
[[ �c�d�e�@�e�m ���K����-�P]]
�@�����ŁA�c�d�e�@�e�m��`�̗��K���Ƃ��悤�B
�y���z�@�ɍ��W�|�������W�ϊ��̂c�d�e�@�e�m�������`����B
- �@�@���ʍ��W�n
- �A�@�n���V�^�ɍ��W�n
�@�@(�ԓ����ܓx�Z�x�A���o����)
- �B�@���w�^�ɍ��W�n
�@(�V��:�k�ɂ��ܓx�Z�x���ɂ�180�x����o����)
�@�ȏ�̗��͢���w�̗��H��Ƃ�����ۂ̔����͐������B�������A���裂Ə̂��Ċ��ɐ������ꂽ�z�����������Ģ�`���ɕ������
'DEF FN������(�p�����^�[���X�g)='
��t���룂Ƃ����̂ł͑S�����K�ɂȂ�Ȃ��ł͂Ȃ����B��`����ɓ������Ă̐��w�I��͏���������DEF FN��`�̎��̂Ȃ̂ł���B�����炱��BASIC�̃}�j���A��������������ǂ�ł�DEF FN�͎g����悤�ɂȂ�Ȃ��̂��B
�@���̖��͍X�ɁA�w�I�ȍ�}����Ă̏������Ȃ��Ȃ��t�����A�㐔�I�Ɉꎟ�ϊ��Ȃǂ���̃A�v���[�`�̕����ϊ������P���ɂȂ�g�p�ɓK���Ă���B�����̉������Œ�`���Ĕ�r���Ă݂�Ɨǂ����낤�B�S�ی�����}�ʼn����Ĉ�{�ɍ����ł�����͂Ȃ��Ȃ��̃x�e�����Ȃ̂��낤�B1950�N��ȍ~���܂�̕��͐��w�Ɏʑ��ƈꎟ�ϊ��A�W���Ȃǂ��h�T�b�Ɖ������Ă��邩�礐̂̃e�L�X�g���Ђ�����Ԃ��Ƃقڂ��̂܂܂̉������邱�Ƃ������B����ȑO���܂�̃I�W����͢���͂œ�֓˔j��������������A�d���Ȃ����������߂ĔF�����Ď��M�r������̂͗L�Q���v�����瑁�߂Ɏq�������̎Q�l����q��������悢�B�n�q(�I�y���[�V�����Y����T�[�`)���́A�k�o(���j�A�[��v�����j���O:���`�v��@)���́A�V�L���@���̂Ɩʔ������ȍ��ڂ�����ł��ċ����������邪�A�������ꗥ�ɐ��k�����ɋl�ߍ��碐��w�D�����������̂��낤������w�������������̂��낤���A��������肾�B������͂ł������nj�͌���̂��C���I��Ƣ�w�^�̉��D����Ƃ��r�ׂĂǂ��炪����w�I�v�l�ͣ��g�ɂ����ƌ�����̂��낤���B�G�b!�q���̍������K��Ȃ�����!?��������܋����Ă�16�N�҂��Ă�킯�ɍs���Ȃ�����A�Ԓ̃r�[���P�{�Z�b�g�̒l�i�ŎQ�l������ɓ�����낵���B���ȏ��Ƃ͈���ēǎ҂̋����̂Ȃ����͔̂p��A�ʔ����̂��Ĕł��d�˂Ďc���Ă���B
�y�T�z�c�d�e�@�e�m �������p�̋�̗�
�@���Ă���܂łŤDEF FN �����쐬�ɂ��Ă̊�{�I������I�����BDEF FN ���K�v�ɂȂ�Τ���̓��e��~�����Ĕ����������Ē�`����悢�̂ł��邪�A�ǂ��ł��g�������ȏ�����I�����⤓��ʂȗp�r�ւ̓K�p�ᤂ����Ђƃq�l�����������Ȃǂ���̓I�Ɏ����Ă������������낢�뉞�p����W���₷������e�l�̕W�����C�u�����[���\�����₷���Ȃ�̂ōX�ɐ،��̎�قȂ鉞�p��������Ă����B
[1]�@�����@���̊��p�Ƣ���̊p�x��A����̕Ӓ���T�O�ւ̊g��
�@�O�p�`�̓�ӂ̒����ƈ���̒��_�̊p�x����A��ӂ̋��p�����߂�ꍇ�A�����@�����狁�߂邱�Ƃ��֗��ł���B[�}�X]�Ɏ����O�p�`�`�a�b�ɉ��Ċe���_�̑Εӂ̒��������ꂼ�ꂁ,��,��,�O�p�`�ɊO�ڂ���~�̔��a���q�Ƃ���Ƃ�,�e�ӂƊp�x�̊ԂɈȉ��̓��������藧��(�ؖ���)�B
�@�@(�ԓ����ܓx�Z�x�A���o����)
�@(�V��:�k�ɂ��ܓx�Z�x���ɂ�180�x����o����)
| a �\�\�\�\ | b ���\�\�\�\ | c ���\�\�\�\ | �@ ���Q�q |
|---|---|---|---|
| sin �` | sin �a | sin �b |
�@���̊W�𢐳���@����ƌĂԖ�ł��邪�A���̓��̈�𖢒m���ɑI��ŎZ�o����z�����`�ɕό`�����DEF FN�����Ƃ��Ďg����B
�@�@�@�@�@�@��
sin �`���\�\�\ sin �a ������
�@�@�@�@�@�@��
�`��sin-1(���sin �a�^��)
�b���Q�ڂq�|(�`�{�a)���Q�ڂq�|{sin-1(���sin �a�^��)�{�a}
�ł���B����͐�قǂ��A�[�N�T�C�����������̂܂܈��p�ł��邩��
4010 DEF FNSINANG(A,B,TH)=FNACSIN(A*sin(TH)/B)
4015 DEF FNSINANGC(A,B,TH)=PAI#-FNACSIN(A*sin(TH)/B)-B
 �ɂ���ā}��/�Q(�}90�x)��l��Ƃ��锟������`�ł����B
�ɂ���ā}��/�Q(�}90�x)��l��Ƃ��锟������`�ł����B�@�w�I�ȍ�}�ɂ���@�͐l�Ԃ���Ƃ����ł͕�����₷���Ę_���G���[�̔�����}���邱�Ƃ��ł���B���̍ہA���߂�p�̕��������������ɂ���ꍇ�ɂ́AIF THEN �ɂ���ĕ����ʂɕ����ĂR�p�`�������āA��ŕ���������������t����̂��I�[�\�h�b�N�X�Ȍv�Z�@�ł���B�Ƃ��낪�R���s���[�^�����͂��������w�I���������A�ŏ��������:�ɐ����������đ㐔�I�Ɉ��������K���Ă���B���̓_�Ţ�Ȃ܂������𗘗p���Ȃ��� IF THEN �����č����@���̗p����̂͊w�I�����Ƃ̐ܒ��ł��܂�X�}�[�g�łȂ���̂ł���B
�@[�}�X-b]�ő㐔�I����̕�����������Ă݂悤�B�I�������A���̕Ӓ��ƕ��̊p�x�̓����ɂ�萳���̔�����ł��ĕ֗��ł���B�ӂ��ɕ������̒��������e���āA�p�x���v���������������肪���A�E��肪���̍������W�n�Ƃ��悤�B��������ƕӂ����������̏ꍇ���܂ł͎O�p�`�̒��_�̊p�x�ł������a�́A�V��̊p�x�v���ł͢��p������ɂȂ�A�����Ɠ������̊p�x���̗p�����B��p�̂������͓��l������Z�o�l�͌����ɐ������ɂȂ��Ă���B�����A�Ӓ����Ɗp�x�a��㐔�I�ɕ��������߂Ĉ����A�Z�o�l�ł���p�x�`���㐔�I�ɕ���(����)�t�������l�������āA������S�����ꏈ���ɂ��邱�Ƃ��ł���̂ł���B
[2] ��Q�]���@���̊��p�Ƣ���̊p�x��A����̕Ӓ���T�O�ւ̊g�� <5.2>
�@�}�Y�̎O�p�`�Ŋe�ӂɂ�����2����2�{��2�|�Q���� cos �b
![���̕Ӓ��F�]���@��](./fig6.gif) �̊W�����肱����Q�]���@����ƌĂԂ��A�b���O �� �b���� �ł͂Q��@��:(�`�}�a)2���`2�{�a2�}�Q�`�a:�Ɠ����ʂł���A�b����/�Q�ł̓s�^�S���X�̒藝���̂��̂ł��邩�猵���ȏؖ��͎Q�l���ɏ���Ƃ��Ă��A���������ȋC�����Ă��邾�낤�B
�̊W�����肱����Q�]���@����ƌĂԂ��A�b���O �� �b���� �ł͂Q��@��:(�`�}�a)2���`2�{�a2�}�Q�`�a:�Ɠ����ʂł���A�b����/�Q�ł̓s�^�S���X�̒藝���̂��̂ł��邩�猵���ȏؖ��͎Q�l���ɏ���Ƃ��Ă��A���������ȋC�����Ă��邾�낤�B�@�����ł͎O�p�`�̓�ӂ̒����ƁA���̋��p�������Ă���ꍇ�̖��m�̂P�ӂ̒��������߂锟�����`����B����͗��ӂ̕��������Ƃ�Ηǂ�����
4110 DEF FNCOSLEN(A,B,TH)
�@�����@���Ɠ��l�A�������ɂ��Ă̘_�c������ƁA���ʓI�ɂ�͂蓯�ꎮ�ŏ����ł��邱�Ƃ��킩��B�ӂ��̕��̕Ӓ����l�����Ă��Acos�̊p�x����p�ƂȂ��� COS(��-TH)���|COS(TH) �Ƃ��ċɐ����t�]���邽�ߎZ�o���Ƃ��Ă͑㐔�I�ɑS������ƂȂ�̂ł���B���̌������������Ƃɂ���āA���Z�𐳑��ƕ����ɕ�������K�v���Ȃ��Ȃ����B
�@�ȏ�̂悤�ȑ�ʂ̉�͏�P�s�ɋl�܂��Ă���ꍇ�A���C�����ꌩ���ē������̑S�Ă𗝉����邱�Ƃ͕s�\�ɋ߂����A��ꌩ���ĉ���Ȃ����C���͎g��Ȃ���Ƃ������j�͖��炩�ɍs���߂��ł���B�W�����C�u�����[�Ƃ��đS�����`�ŏ������Ă����̂ł���A����������e�̕�����₷�����̂ɓ��ꂷ��H�v�͕K�v�ł��邪��͂ƃC���^�[�t�F�C�X���L�����h�L�������g���������Ă����Ώ[���֗��Ɏg����ł͂Ȃ����B���Z���e�̕�����₷���̓T�u���[�`�������ƕς��Ȃ��B
4100 ' ��ӂƂ��̋��p�����Ӓ�������:�]���@��
4110 DEF FNCOSLEN(A,B,TH)=SQR(A*A+B*B-2*A*B*COS(TH))
4140 ' �O�ӂ����p������
4150 DEF FNCOSANG(A,B,C)=FNACSIN(SQR(1-((A*A+B*B-C*C)/A/B/2)^2))
4180 ' ��ӂƂ��̋��p���瑼�̈�p��������:(�]���@��+�����@��)
4190 DEF FNTRITH(A,B,TH)=FNSINANG(A,FNCOSLEN(A,B,TH),TH)
[�T-(2)-3]�@�O�Ӓ����璸�_�p�����ށF(��Q�]���藝)
�@�Ȃ��A�O�ӂ̒�������e�p�x�����߂锟������`���Ă������B
�@�@�@�@�@�@��2�{��2�|��2
cos �b���\�\�\�\�\�\�\�\�\
�@�@�@�@�@�@�@�Q����
cos �b��sin(�b+��/�Q)�@�@������
�O�o�̃A�[�N�R�T�C��������A�[�N�T�C�����������p����悢�B�A�[�N�R�T�C�������́}��/2����ʂł��Ȃ�����A�����ł͊����ăA�[�N�T�C�������ŃA�[�N�R�T�C�������߂Ă݂悤�B
sin2�b��1�|cos2�b
�@�b��sin-1(SQR(1-cos2�b)) �ł���A��� cos �b �̒l�����߂Ă��邩�� DEF FN �����͈ȉ��̂悤�ɒ�`�����B����� COS �̋t����������A
�@cos �w��cos(�|�w)�@�ł��萳���̕�������ʂł��Ȃ����炱�̎��������Ă������̊p�x����`���邱�Ƃ͂ł��Ȃ��B
[�Q-(3.b)]�@�O�p�`�̎O�ӂ���ʐς������i�⑫�߁j
�@���L���̕⑫�F�O�p�`�̎O�ӂ���ʐς����߂�͓̂y�n���ʂ̊�{�D�O�p�`�̗��ގ��p��ɂ͌������Ȃ��D
�@�ʐώZ�o���j�Ƃ��ẮA���]���藝����P�p�̗]��cos�����߁A�����sin�Ɋ��Z�A�p�����ޓ�ӂ��C���Ɗp�b�̐�������A�O�p�`�ʐρ�������sin(��)�^�Q �Ƃ��Čv�Z����.
���Ȃ킿
�@��2����2�{��2�|�Q������cos�b�@�c�c�c(���]���藝)���
�@cos�b��(��2�|��2�|��2)�^�Q�����
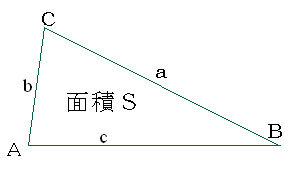
|
| �Ӓ������ꂼ��a,b,c�A ���̑Ίp�����ꂼ��A,B,C�Ƃ���D |
�@sin2�b�{cos2�b���P�@�c�c�c(�O�����̒藝�̌n)
�@sin�b��sqrt{�P�|cos2�b}�@�ƂȂ邩��A
�@sin�b��sqrt[�P�|{(��2�|��2�|��2)�^�Q�����}2]
���ʐ�S��������sin�b�^2�@�ƂȂ�B
��������[�U�[��`�����������
DEF FNSINC(a,b,c)
�@�@�@�@=sqr(1-((c^2-a^2-b^2)/a/b/2)^2)
DEF FNSQUARE(a,b,c)=a*b*FNSINC(a,b,c)/2
�ƒ�`����A�g�p����
PRINT FNSQUARE(a,b,c)
���Ɣ��ɊȒP�ɂȂ�B
(���L���̕⑫�F)
�ʐρ�sqrt{���(���|��)(���|��)(���|��)}
�@����(���{���{��)�^�Q�@�@�@�@�@�c�c�c�c�c�c�c�i�w�����̌����j�����̂܂ܔ�����
DEF FNS(a,b,c)=(a+b+c)/2
DEF FNSQUARE(a,b,c)=sqr(FNS(a,b,c)*(FNS(a,b,c)-a)*(FNS(a,b,c)-b)*(FNS(a,b,c)-c))
�Œ�`����B�g�����͑O�߂Ɠ����B
�@�L���������̂邩�A������Ղ��Z�o�������̂邩�̑I���̓N���C�A���g�̎w�肪�Ȃ���v���O���}�[�̍D�݂����A�ǂ���̎Z���Ōv�Z���Ă��A���R�A���ʂ͓����ł���B
[�Q-(4)]�@��Ӓ��Ƌ��p���瑼�̒��p��
�@�O�p�`�̓�ӂ̒����Ƃ��̋��p���瑼�̒��p�����߂�̂́A�]���@���Ɛ����@�����c�����ėp���āA�悸���m�̂P�Ӓ������߂āA����ɂ�葼�̒��p�����߂�悢�B��`���� 4190�s�ł���B
[�R] �@�g���C�A���h�G���[�@�ɂ��t�����ߎ�
�@�L�q�ł���t���������݂��Ȃ��ꍇ���������(��)���O�̍�����v�Z�ŋ��߂邱�Ƃ͍���ł��邪�A�v���O���}�u���̌v�Z�@(�d����܂�)���g���ė͂Â��Ŏw�萸�x���̋ߎ��l���Z�o������@���������l�����Ă���B���̈�ł���A�P���ȃA���S���Y���ł���Ȃ��獂���x������x���Z�̊��҂ł��颃j���[�g���̋����@��̗�ɂ��ĐG��Ă��������B[�R-(1)]���[��(�N������)����
�@���������̎������w���~��Ăm�N�̕��������ŕԍς���ꍇ�́A���N�ԍϊz�`�Ƒ��ԍϊz�s�����߂�Ƃ����͖̂��炩�ɂR�Ɨ��ϐ��̔����ł���B
�@�@�@�@�@�@�@��
�`���\�\�\�\�\�\�\�\�w�@�@�c�c(��<>�O)
�@�@�@�@�P�|(�P�{��)-N
�`���w�^�m �c�c(�����O)
�s���`�E �m
�@�܂����m�����m��w,���Ƃ����ꍇ�����l�ɂR�Ɨ��ϐ��̔����ł��邪�A���ɂ��Ă͋L�q�ł���z�������Ȃ��̂Œ��ڌv�Z�ł��Ȃ��B��������߂̢�j���[�g���̋����@��̗��ɉāA�m�Ƃw�ɂ��Ď��������
�@���������̎������w���~��Ė��N�`�����ԍς���ꍇ�A���N(�m)�ŕ����I���邩!�Ƃ�������
�@�@�@�@�@�@�@�@�@�� �w
�@�@�@�@����(�P�|�\�\�\)
�@�@�@�@�@�@�@�@�@�@�`
�m���|�\�\�\�\�\�\�\�\�\�\�\
�@�@�@�@����(�P�{��)
�@���������̎�������Ăm�N�Ԃɂ킽�薈�N�`�����ԍς���ꍇ�ɁA���������w���~����邾�낤���H
�@�@�@�@�P�|(�P�{��)-N
�w���\�\�\�\�\�\�\�\�`�c�c(��<>�O)
�@�@�@�@�@�@��
�w���m�E�` �c�c(�����O)
�Ƃ����R�{�P�̔������l������B
XXXX DEF FNLOANX(A,N,R)=(1-EXP(-N*LOG(1+R)))*A/R ��
XXXX DEF FNLOANA(X,N,R)=R/(1-EXP(-N*LOG(1+R)))/A
XXXX DEF FNLOANN(X,A,R)=-LOG(1-R*X/A)/LOG(1+R)
�̎O�{����{���ł��邪�R=0�� R=A/X�����ٓ_�ɂȂ��ĕʂ̎��ƂȂ�R<0��܂��� A/X<R �͒�`��O�ł���B
���O�`�F�b�N�Œ�`��O��r������K�v������B�܂������O�͕ʂ̎��Ȃ̂ŁA��Ԑ�ւ��X�C�b�`���e���ɐ݂��āA�_�~�[�������ăG���[��������Ĥ�l�����߂�B
4310 DEF FNLOANX(A,N,R)=
�@�@�@�@�@-(1-EXP(-N*LOG(1+FNNZ(R))))*A/FNNZ(R)*(R<>0)-N*A*(R=0)
4320 DEF FNLOANA(X,N,R)=
�@�@�@�@�@-X*FNNZ(R)/(1-EXP(-N*LOG(1+FNNZ(R))))*(R<>0)-X/N*(R=0)
4330 DEF FNLOANN(X,A,R)=
�@�@�@�@�@LOG(FNNZ(1-R*X/A))/LOG(1+FNNZ(R))*(R>0)-X/A*(R=0)
4350 DEF FNNZ(R)=R-(R=0)
�@���ۂɃ��[����g�ޏꍇ�ɂ͌������ƃ{�[�i�X�����������āA�N���͕����ł��N�����̌v�Z���P���ł���A�X�Ɏ����������グ��S���a����v�����ꂽ�肵�ĕ��G����ƂȂ��ďڍׂ̕ԍϋ��z�͋��Z�@�ւ̔��s����W���ԍϕ\�ɗ��邱�Ƃ��قƂ�ǂȂ̂�����ǁA��{�̌v�Z�������̌v�Z���ōs�Ȃ��ĕԍόv��̃V�~�����[�g�����Ă������Z�@�ւ̏o�������̎��������Ȃ�悭�����ł��Ď��M�������Č���i�߂邱�Ƃ��ł���B
�@���̏������v�Z�̎��������̑傫���T���ृN���W�b�g�v�Z�ȂǂɓK�p����Ƥ�ԍύs�ז��̒P���v�Z�ɂ���Ď����������ƂȂ閯�@491���̌v�Z�����Ƃ̌덷���ڗ����Ă��邩�璍�ӂ��K�v���B
�@�]�k�����ɢ�g�[�^����V�X�e����̊ϓ_���碃p�\�R���p�T�������\�t�g����l����Ƥ�P�ɗ��������@�Ȃǂ̊��K�p���������m�F��ԍόv�揑����邾���ł́A�ǂ�Ȃɍ��@�\�ŃX�}�[�g�ȃ\�t�g��������Ƃ���ʼn����̔�Q�ҋ~�ςɂ͂Ȃ�Ȃ����Ƃ��w�E�������B
�@�T�����N���W�b�g�����}�N���ł݂�A�؋��������ł��邩�̐�`�Ǝ���ɋ����ɂȂ鏎�������Ƃ������Љ�̔��f�ł��邱�Ƃ͋^���Ȃ����A�~�N���ŌX���݂�ƁA�����J���đ҂����̕@��Ɏ���߂Â������̂悤�Ȕ��Εa�I�Ȕ�Q�҂�����킯�ŁA�䓖�l�����o�I�ɂ��̐�������ς��錈�ӂ����Ă��Ȃ��̂ɁA���͂ŏ���ɉ������Ă��ق�100���Ĕ����Ă��Ƃ̖و���ƂȂ��ĉ����ɗv�����܂��̓w�͂����A�ɋA���̂��o�����ł���B�����̂��͓̂��ʂ̈��ӂ��Ȃ�����u�Ȃ����͐U��Ȃ��I�v���R���鎖���̑O�ɗ��������@���̍������J�b�g���̂ƃ��b�g���炵�����݂��Ģ�ԍόv�揑������肻�̗]�����@�I�ɓ��ݓ|���Ă����v���Z�X�������[�`�������Ă��邩��A�^�ʖڂɑ��k�ɂ̂��Ă����c�̂�ٌ�c�̗͓Y����Z�p�I�ȍ���͂��܂�Ȃ��̂ł��邪�A���l�������̐ӔC�Ƃ��Ď��o���Ď�����}��Ȃ�����Ĕ���h����͂Ȃ��B�����̗F�l�Ŗ��N���I���:BS�c�c�cBS���i�撧����Ƃ��Đ������k���������Ă���D�G�Ȍ��Z�p�҂�����B���ꂪ����̃T�����\�t�g�ő��k�ɂ̂袈����T�����ގ��̖��l��ɍՂ�グ���ċ��邪�A���܂�ɑ����Ĕ��ɕ��ꂩ�����đΏ����j�����߁A���X�������������Ȃ�ɂ��Ă��A���l�̎��o�𑣂����ꂱ��̑[�u�ɏd�_���ڂ����̂������B���m�F��ԍόv�揑�Ȃǂ͏ڍׂȍ쐬�@(����@)�������āA���l���g�ɍ�点�āA���҂Ƃ̌������Ȃ͂��邪�K�����l���S�Ői�߂����邱�Ƃɂ����B��������ɂ��₩�Ɂw���̋ݏ͂́�����Ɓ~�~�g�̊����o�b�`�Ȃ�ł��x�ȂǂƢ���������̂����Ŕ̗͂ŕK���ɕ��������ČJ��Ԃ��������Ď��ɂ͢���̖������v���w�J���̎m�x�������݂��̎g������ŏ������ꂵ�߂�Ƃ͏�Ȃ��I��Ȃǂƈꔭ���܂���(���k���ē��肪�_�炩���Ȃ����Ƃ�!)�������@�̓��ӂ�Ƃ������v���Z�X�̒��Ŕ�Q�Ҏ��g�����炵�Ď����ċN�𑣂��A����ł���������l�̂Ȃ��ꍇ�ɂ͉Ƒ�����̋t�O���蔼�̍����܂Ŗʓ|�����悤�Ƃ�����g�[�^����v���O������̂Ȃ��ł̕⏕�c�[���Ƃ��ē��퐶������̃p�\�R����\�t�g���l����ׂ��Ȃ̂��B����̓J�X�^����\�t�g�𐿂������V�X�e����n�E�X�̎��_�Ƃ͂��Ȃ�Ⴄ�����̎��_��ł���B
�@�܂��A���̔����͑ݎ̗�������ւ���ƁA���̂܂ܔN���v�Z�ɂȂ�B���Ȃ킿�A�M����s�ȂNj��Z�@�ւɂw���~���������ŗa���āA�m�N�Ԃɂ킽��N�������ꍇ�A���N�̔N���z�`�����ށI�Ƃ������ɗ��p�ł���B
[�R-(2)]�@���s����@�͓d�Z�@�Ɉˑ��I
�@���āA��̃��[���v�Z�ŁA��������������ɂȂ邩���Z�o���Ă݂悤�B�L�q�\�ȋt���������݂��Ȃ������̍����R���s���[�^�ɂ�鎎�s����@��p���ė͂����ŋ��߂悤�Ƃ����̂�����A��v�Z�ł̋t�Z�͌�Ɩւ邪��������f�@�\�̂���v���O�����d���R���s���[�^�̉��K�ۑ�Ƃ��Ă͒��x�荠�̉ۑ�ł���B���Z�����𒊏ۉ����� DEF FN �ɂ͈�w�K������ł���A���̃v���O���������m�ɓ����ƃr�M�i�[�͑�ςȎ��M�����B�@�����A�w�E���Ēu���ׂ����Ƃ�����B���ۂɂ͋L�q�ł���t���������݂���̂Ɏ��s����@��p����̂͐��w���s���o���Č��\�p�Ƃ��Ă͂��Ȃ�p�����������炻���͐T�d�ɒ��������w�ʂɊm�F����Ȃǂ�����������ł���B�����ɂ���Ă͂��Ȃ萸�x�̍����ߎ����̑��݂��m���Ă���B�A���A�\�t�g�͌��ʃI�[���C�̐��E����������c�[���Ƃ��Ă͎d�l�����Đ��m�ɓ����Β����͉��ł��悢�Ƃ����̂������ł���B���l�̕]���̂��߂Ƀ\�t�g�����̂ł͂Ȃ��̂��B�����������c�ɂ͌��킵�Ă�����(�Ƃł������ċ������Ă����Ȃ��Ƣ���w���l�ԣ�̎��ɂ̓E�b�J������o���Ȃ��I���݂��Ȃ��Ƃ͎v���̂�����ǂ�������t��������������S�����i�T�C�I)
�j���[�g���̋����@�ł̔������p
 �@���s����Ƃ͂����Ă��A���̑Ώۂɂ���ėl�X�ȕ��@���l������B
�@���s����Ƃ͂����Ă��A���̑Ώۂɂ���ėl�X�ȕ��@���l������B�@ ���̊܂܂�Ă����Ԃ������������ĕВ[����l���v�Z���āA�����ɋ߂��l�̕t�߂��X�ɍׂ����������Ďw��덷�͈͓��̉����߂餂Ƃ������@�͕����̍��������o�������ł���B
�A ���̒l�𐄑����Ĕ����ɓ��Ă͂߂āA���̒n�_�ł̐ڐ������������߁A���̐ڐ��̍���V���ȍ��̐���l�Ƃ��āA�덷�̑傫���ׁA�ݒ�͈͂��傫�Ȍ덷�ł���A�V���Ȑ���l�����Ƃɍēx�ڐ��������̌v�Z���J��Ԃ��Ƃ�����������j���[�g���̋����@��ƌĂ�čL���g���Ă���B���̕����͉��ւ̎����������ăA���S���Y�����P���Ȉ�d���[�v�Ȃ̂ŏd��ł���B���_�͕��������������Ă��܂����Ƃł���B������A���������P����,�P�ꍪ�ł��邱�Ƃ��������Ă���ꍇ�ɍ̗p����Ƃ��A�S��`������ď��Ԃɍ������߂Ċm�F����Ȃǂ̍H�v�̂��Ƃɍ̗p�ł�������ł���B���̕��������Z�������̐��w�̎Q�l���Ɍf�ڂ���Ă����B�ŋ߂̍��Z���͊w�Ԃ��Ƃ������đ�ς��B
:�����o��:
�@��d�q�v�Z�@�̐��w��������̉�@��j���[�g���̒����ߎ��@������Њ���V�����[�~�M�1975/7����|�V������
������(��)�̑I��
�@�j���[�g���@�ł͂܂���ӂ���
��(��)���O�@�Ƃ������������������Ă��̂�i�ɂ�����ڐ������������߂�B
�@��i�ł̐ڐ��̌��z�����߂�ɂ������Ĕ����ȋ������ͤ�v�Z�@�ň����s����L���̒l�ł��邩�礂�i�̗����Ɂ}�����ꂽ�_��ݒ肵�āA�X�������߂������덷����Ȃ��\���������B
�@������ڐ����z��
�@���@�@�@�@�@�@�@�@�@��(��i+��)-��(��i-��)
�\�\{��(��i)}���\�\�\�\�\�\�\�\�\�\�\ �� ��
�@�����@�@�@�@�@�@�@�@�@�@�Q ��
�@�ڐ���������
��(��)�|��(��i)�� ��(���|��i)
�@���̕������� ��(��0)���O �̓_��0���V���ȍ��̐���l�ł���B
�@�@�@�@�@�@�@ �D
��0�|��1�� �|��(��i)�^��(��i)
�@���̎��̒l�͐��荪�̏C���l�ł���B���ꂪ���p��[����������ΐ����Ƃ𒆎~���Ă悢�B���̔���� IF THEN �ōs�Ȃ��ă��g���C����[�v���`�����āA���̎������܂�ł���B
�ӊO�ɊȒP�I���[���������v�Z�ւ̢�j���[�g�������@��̓K�p
�ȏ�̃A���S���Y�������[���v�Z�ŋ�̓I�Ɏ��������Ă݂悤�B
�@�O�o�̎����A�Q���̍������߂�`�ɕό`���� ��(��) �Ƃ��邪�A�w���萔�Ȃ̂Ł@��(��)��FNLOANX(A,N,R)-X �ł���B
5100 X=1000�@�@�@'�ؓ��z(����)
5110 A= 120�@�@�@'�����ԍϊz(����)
5120 N= 10�@�@�@'�ԍϊ���(����)
�ȏオ��ӂ̗^�l�ł���B�����薢�m���̗������������߂�BINPUT���[�`���ł����̒l��^����Ǝ��p���C���ƂȂ�B�g��������l������Ə��s���œ��͂ł��邱�Ƃ��]�܂����B
5130 IF A*N<X THEN STOP�@�@�@�@�@�@�@�@�@�@'�L�蓾�Ȃ����l�̃g���b�v
5210 DEF FNLOANX(A,N,R)=
�@�@�@�@-(1-EXP(-N*LOG(1+FNNZ(R))))*A/FNNZ(R)*(R<>0)-N*A*(R=0)�@'������
5220 DEF FNNZ(R)=R-(R=0)�@�@�@�@�@�@�@�@�@�@�@�@�@�@'0��1
'
5240 DLT=0.00001�@'�����ψʕ����`
5230 LIM=DLT�@�@�@'�덷���E���w��
�@�������q�́A�O���傫���A�`���w�����������̂͊m���ł��邩��A
�@�ŏ��̐���l�����ɒ��Ԃ̂`���w���Q�ɑI�ԁB
5300 R=A/X/2�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@'������l
'
5400 *RETRY�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@'�� R�̏C���l��D
5410 D=-2*DLT*(FNLOANX(A,N,R)-X)/(FNLOANX(A,N,R+DLT)-FNLOANX(A,N,R-DLT))
5420 R=R+D�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@'R�̐V����l
5430 IF ABS(D)>LMT THEN *RETRY�@�@�@�@�@�@�@�@�@�@�@'�덷�͈͊O�͍Čv�Z
'
5500 PRINT "��������";USING "###.### [%]";R*100�@ �@'[[��!!]]
5510 END
�@�j���[�g���@�ł̎������Z���͂킸���R�`�S�s�ɉ߂��Ȃ����A����̎��s�ɂ���Ăق�̈�u�ʼn��l����B������e�X�g���Đg�ɕt���Ă������l�͑傫���B�i[LIST2]�Q�Ɓj
[�S] �k�b���U���g������
�R�C��:L�ƃR���f���T�[:C�ɂ�鋤�U��H�̋��U���g��:FRQ�́A�T��
FRQ=1/(2�~�~SQR(L�~C))
�ł��邩��A������`�����
DEF FNFRQ(L,C)=1/SQR(L*C)/2/PAI#
�ƂȂ�B����́A�X�ɂk,�b�����ꂼ�ꖢ�m���Ƃ��锟���ɕό`���Ďg���邱�ƂɂȂ�B
�@�����e��CAP��
DEF FNCAP(FR,L)=1/4/PAI#/PAI#/FR/FR/L
�@�����C���_�N�^���XLI��
DEF FNLI(FR,C)=1/4/PAI#/PAI#/FR/FR/C
�@���̎�̔����́A�b�q���U�@�A�{�[�f���}�A�i�C�L�X�g���}�A�e��t�B���^�[�ȂǁA�v�W�̌v�Z���قƂ�ǖԗ�����B�����ɏ������߂��v�Z���قƂ�ǂ��̂܂܂� DEF FN ��������Β�`����Ă��܂��̂�����A����ȒP���Șb�͂Ȃ��B
[�T] �g����I�ėp�c�d�e�@�e�m ����
�@�Ō�ɂǂ��ɂł��g��������DEF FN�����������Ă����B�ʏ�̍�Ƃ͂���܂łɏЉ����Ƃ��킹���̒��x��DEF FN�̃T���v��������ƁA�����œƎ��ɍ쐬����DEF FN�͎又�����[�`���ȂNjɂ߂Č���ꂽ���̂ɂȂ�A���͕����ȂLjꕔ�����ɂ�闬�p��g�����͈̔͂ő����͂��ł���B
�@STR$(X)�����͕����̐����ɍS�炸�P���̕�����������B����������蕥�������ꍇ�́A
�@ �������ɂQ���ڈȍ~���璊�o����B���̏ꍇ����������̂Ă��ĕ����͕�����Ȃ��Ȃ�B
6010 DEF FNNS$(X)=MID$(STR$(X),2)
�A ���ƂO�̏ꍇ�����Q���ڂ��璊�o���A�������͎c���B���̌^�͕������𗘗p����ꍇ�ɍ̗p����B
DEF FNNS$(X)=MID$(STR$(X),2+(X<0))
�B ���l�̒�`�悪�O�`�X�͈̔͂Ɍ����Ă���ꍇ�� HEX$(X) �����̂܂ܗ��p�ł���B
�@���̔�����������p���邩��ėp���̓_�Ň@���̗p����̂�����ł���B
�@�����l�w���E�l�߂m���̕�����Ƃ������P�o�C�g����:�a���Ŗ��߂锟���́A��̕���������锟�������p���Ĉȉ��̗l�ɒ�`����B
6020 DEF FNSTRB$(X,N,B$)=RIGHT$(STRING$(N,B$)+FNNS$(X),N)
�@�����l�w���E�l�߂m���̕�����Ƃ�����"0"�Ŗ��߂锟���́A��̋��w�蕶����Ŗ��߂锟�������p���Ĉȉ��̗l�ɒ�`����B
6030 DEF FNSTRZ$(X,N)=FNSTRB$(X,N,"0")
�@�����l�w���E�l�߂m�{�P���̕�����Ƃ��č��[���Ƃ�����"0"�Ŗ��߂锟���́A��̋�"0"�Ŗ��߂锟�������p���Ĉȉ��̗l�ɒ�`����B
6040 DEF FNSTRSGN$(X,N)=MID$("+-",1-(X<0),1)+FNSTRZ$(X,N)
�@�ʐM����Ȃǂł̃t�H�[�}�b�g�̋�J�͌�������B
�@16�i�����l�w���E�l�߂m���̕�����Ƃ�����"0"�Ŗ��߂锟���͈ȉ��̒ʂ�ł���B
6050 DEF FNHEXSTR$(X,N)=RIGHT$(STRING$(N,"0")+HEX$(X),N)
���������m���ɂ܂�߂锟���͈ȉ��̒ʂ�ł���B
6060 DEF FNRND.$(X#,N)=FNNS$(INT(X#*10#^N+.5)/10#^N)
�@���l�̏����w��̔ėp�������Ȃ����߂ɁA�e�l�ł��낢���J���Ă���B�Ȃ��ɂ� MS-DOS�� RAM�f�B�X�N��ݒ肵�āA������g���� PRINT USING "#.##";X �ŃV�[�P���V�@����t�@�C���ɋL�^���āA���߂ĕ�����f�[�^�Ƃ��ēǂݏo���Ƃ����܂��܂����v���Z�X�Ő��l�̏����w�蕶������쐬������������B����͔z��f�[�^�𑽗p���Ȃ���Εs�g�p�̈�ƂȂ�128[KB]���L���邾���Ť�o�O�̂Ȃ������w�肪�ł���̂����� RAM��640[KB]�̃V�X�e���ł͎��p�Ƃ��đÓ��ȕ��@�Ƃ����ׂ��ł���B�����A������DEF FN�̏Љ�̃y�[�W�ł���ADEF FN �����ō\�����Ă݂悤�B�w�����l�A�m���S�����A�l�������������Ƃ���Ƃ��A���l�����w�蔟�� FNRDX$(X,N,M) �͈ȉ��̗l�ɒ�`�ł���B��`�ɋ�J���Ă��A���C�u�����[�ƂȂ�����͒����Ɉ�؎��G���K�v���Ȃ��̂����炻�̌�̌����͂悢�B
6070 DEF FNRDX$(X,N,M)=MID$(FNRDS$(X,N,M),INSTR(FNDP$(X),"."),N-(M>0))
6080�@�@DEF FNDP$(X)
�@�@�@�@�@ =MID$(STR$(X),2+(X<0))+STRING$(-(INSTR(STR$(X),".")=0),".")
�@�@�@(�����_�t�� ������)
6090�@�@DEF FNRDS$(X,N,M)
�@�@�@�@�@ =STRING$(N-M+(M=0)," ")+FNDP$(X)+STRING$(M,"0")
�@�@�@(�����t�� ������)
�y�Y�z ��ėp�T�u���[�`���vs ��̗D�ʢDEF FN�����
��c�d�e�@�e�m������Ƣ�ėp�T�u���[�`����������r����I�ƌ�����ƁA���ꂱ��t�я��������Đ����ɂ��Ȃ��J����B���ʂɎg����T�u���[�`���ł́A�ϐ��������肳��Ă��܂��̂ŁA�ʂ̃��C�����瓯��̉��Z���ł��邪�ʂ̕ϐ����̏������Ăԏꍇ�ɁA�O�̒l���ꎞ�ޔ�������Ȃǂ̎葱�����K�v�ƂȂ�A�X�ɒl�̎�n�����K�v�ƂȂ�̂ŁA���������ł͕ϐ�������Ȃ� �c�d�e�@�e�m���D�ʂȂ̂͊m���ł���B�@����A��v�Z�̃A���S���Y���ɒ����ɃR�[�f�B���O���ĉ��Z����11�łɒB����v���O�����̋@�\�lj���������|��������e�L�X�g�������[�̋e�ʂ�27�o�C�g�����Ȃ������̂ŁA�S�̂̏������R���s���[�^�����̉��Z�A���S���Y���ɐ����������� DEF FN ���̗p�����B���ʂ͌��A���S���Y���Ɍ��������̂��x�ꂽ���ߐV�K���쓯�R�ɂȂ��Čv������ɑS���Ԃɍ��킸�ɎU�X�̖ڂɂ��������A���e�Ƃ��Ă͉��Z���Ɣ�����`�������ꂼ��P�y�[�W�O��̍��v�Q�y�[�W��ɐ�������āA�������[�e�ʂ�10�L���o�C�g�]�ɂ������A�lj��v���d�l�𑍂Ď�����������őS�ʍ폜����Ă����R�����g���L�ڂ��邱�Ƃ��ł����B���Z�����C���̌��v�҂͂����c�d�e�@�e�m �̌��p����ƌ�������B�������ۂ͢��v�Z�p�̏璷�x�̍���(�G���[�����₷�����j�I��)��ƃA���S���Y�����R���s���[�^�����̃A���S���Y���ɕς������Ƃ�����ł���A�ėp�T�u���[�`�������ō쐬�����Ƃ��Ă��S�y�[�W���x�Ɏ��܂���e�������B
�@���̃A���S���Y���ύX�͎d�l�lj��ύX���������邽�߂ɁA�����̏����ł͊��S�ɍs���l�܂����������[�s���̓˔j��Ƃ��Ă�ނȂ��s�Ȃ������̂ł���A�K�R�����Ȃ��̂ɐ���ɓ��삵�Ă���\�t�g�̎�v�A���S���Y����ύX����̂́A�V���ȃo�O�����̋@�����邾���̋��s�ł���B
�@�K�������v���O���~���O�̐��Ƃł͂Ȃ��e����Z�p�҂��A�����v�Z���������̂܂܃R�[�f�B���O���ăA���S���Y����G���[���N����Ȃ��悤�ɂ���Ƃ������j�͎����Ƃ̕��j�Ƃ��Ă͋ɂ߂Đ��������j�ł���B��v�Z�ł̋��ʏd�����������܂����������ł���Ȃ��ǂ��̂����A����Ă��ď����@�Ɋm�M�̎��Ă�A���S���Y����ϋɓI�ɕ������闝�R�͂Ȃ��B���ꂪ�ǂ�Ȃɗ��j�I������I�A���S���Y���ł����Ă��v���d�l�����Đ��m�ɓ��삷�����͑Ó��ȕ��@�ł���B���������邢�͕���Ƃ����̂͑S���̋؈Ⴂ�ł���B�Ƃ͌����Ȃ���A90߂܂ł�������Ȃ��V���ΐ��\�ƌv�Z�ڎ���̃A���S���Y�����̂܂܂̖c��ȃ��C���Ɗi�����āA�v�킸�����̐����Ţ���ʉ�����Ă��̂͊w�̐��E�Ȃ�ł��˃F��ƙꂢ�Ă��܂����̂��B��d�C������ɂƂ��Ă͎O�p�����́w�g�x������A�����Ă邯�ǁA�y�،��z�͍�}�ōl���邩��90�K�ȏ�̊p�x�͊ᒆ�ɂȂ������ł�����Ɖ����Ă������A�܂��ɂ��̒ʂ�Ŏ��̎����ł������BPC-98�̔\�͂̌��E�ɒ��킷��v���d�l���Ȃ���ΑS�����ɂ��Ȃ炸����ɉ��Z���Ă����̂�����B
�@�Ƃ��낪�A�T�u���[�`�����c�d�e�@�e�m�̋@�\�ɕ���Ĉ�ʉ����āA����[�J���ϐ�����߂āA����ɑ������`�ŏ�����i�߂�`���ɐ�������ƁA�ϐ����m�̏Փ˂̖��ƁA�T�u���[�`���ւ̓��o�͂ł̃f�[�^�̎�n���葱���ƃe�L�X�g�������[����̖��ɏW���B�����A���S���Y�����̗p����ꍇ�ɂ͂c�d�e�@�e�m����D�ʂ��Ƃ��Ăःe�L�X�g��������[������Ȃ��Ȃǂ̕����I�Ȑ����ɂԂ����Ģ���I���ʣ��������܂ł́A����I�ɗD�ʂɂȂ邱�Ƃ͂��܂�Ȃ��̂ł���B
�@�T�u���[�`���̒�`�͎��R�x����������A���̏ꂻ�̏�ɍ��킹�č���Ă��܂��B���̂��Ƃ�������ɈႤ�������o�ė���Ƌ��ʉ�������Ȃ�B
�@�c�d�e�@�e�m������`�ł͈�ʉ����܂ޏڍׂ̌��������߂��邩��A���̌����̒��ŃA���S���Y�����̂����ǂ���āA���̌��ʂ̕������͑傫���̂��낤�B
�@���ǁA���J�ɐv�����v���O�����ł͂c�d�e�@�e�m�ƃT�u���[�`���̑卷�͐��܂�Ȃ����A��͂̎���Č������킹�����ɂȂ�ɏ]���āA�蔲�������܂苖���Ȃ��c�d�e�@�e�m�̕������̕��i���������ɂ����Ȃ�Ƃ����̂����m�Ȏ��Ԃ��낤�B
�@��͂ł̎蔲���́A�s���Ȃǂł��̉��{���̘J�͂�D���B���̈Ӗ��ł͈ꉞ�̉�͂�v������ �c�d�e�@�e�m�����̕���(���_�����)������̒���������ƌ�����̂��낤���B
�@�����̃|�P�R����v���Z�X����p�ɊJ�����ꂽ�R���e�b�N�̂o�b�|�X�W�p���A���^�C���a�`�r�h�b�Ȃǂɂ͂c�d�e�@�e�m�����@�\�͑��݂��Ȃ��B�����ł́A����[�J���ϐ�����߂āA���̕ϐ��Ƃ̏Փ˂ɒ��ӂ��Ȃ��� �c�d�e�@�e�m���̃G�l���M�[���₵���ėp�T�u���[�`�����쐬���Ăc�d�e�@�e�m�ɑウ��ق��Ȃ��̂ł���B
�y�Z�z�킩��Ղ�DEF FN��`
�@���Ȃ��Ȃ�����DEF FN�ɂ��ďd��Ȍ�������Ă���B�wDEF FN��`���́A�ǂ̂悤�ɕ��G�Ȃ��̂ƂȂ��Ă��������Ȃ��B���̃u���b�N�{�b�N�X�ƂȂ�B������`���͂P�s�͈̔͂Ɍ�����c�c�c�BFOR��,IF����p����ΊȒP�ɕ\���ł��邱�Ƃ����G�Ȏ��ƂȂ�����,�Ƃ��ɂ͋L�q�s�ƂȂ����肷��B�c�c�c������Â炭�Ȃ邱�Ƃ͔������Ȃ��悤���B�x(�O�o��v���O���~���O��X�^�C���u�b�N�)�B�@����̓��[�U�[����`����DEF FN�������A�ʂ�DEF FN�������牽�d�ɂ��Q�Ƃł��邱�Ƃ������Ƃ������ߔ�������������Ǝv���B�{�e��U��Ԃ��Ă݂Ă��A����̑����͑��d���p�ɂ���Ď����`���Ă���B�X�̋@�\�����Ԏ��͂���Ȃɕ��G����ł͂Ȃ����A�S��`���\�킷�����e��Ԏ��̘a������`�Ԃ͒P���Ō��ʂ��͈����Ȃ��͂��ł���B�����̓��e���̂����G���Ƃ����̂�DEF FN�Ɍ��炸�����g���Ă����G�ɂȂ邩��{���ʖ��ł���B
�@�����̒�`�撆�̋�Ԃ̐�ւ��ɗp���Ă��题_�����̒l���������ɂ����ő�̗��R�͢���܂�g������Ă��Ȃ����ƣ�ɉ�����'�^'�̏ꍇ��'�|�P'���������Ƃł͂Ȃ����낤���B������������Ɋ�Â��ے�I�]���͏C�������ׂ��ł���B
�@�����܂œǂ�ŗ����ł������� DEF FN�Ɋւ��Ă͊ԈႢ�Ȃ��G�L�X�p�[�g�ɂȂ��Ă���B���܂܂� DEF FN �ɂ��Čn���I�ɐ����������̂��Ȃ������̂�����A����G�Ȕ�����A���S���Y����ǂݔ�����Ƃ���ł��������Ⴂ�͂Ȃ��B�L�q���e�͒��w���獂�Z�P�N�Q�N���x�̐����ł����ȏ���Q�l���Ɠˍ����Ȃ���ǂ݂��Ȃ�����e�ł���B�����A�O�\�H�������߂���Ƃ����Ă̋P���铪�]��������������͂��߂ăg���J�`�Ńu�b�������ċl�ߍ��ސK������Ă����r����Ȃ���ԂƂȂ�B��s�����@�a�`�r�h�b����͢���o�p�\�R����ƕ���œǎ҂̃I�W����x�̍����G���ƕ����Ă���(�s�f�����ŗ����ǂ�ł鎄��'KYON2'�Ȃ��'OJIN2'�Ȃ̂�?!)�B������A�Ⴂ����肩�Ȃ藝��̗͂������I�W����ǎ҂̂����P���̓ǎ҂��V���ɓǂ݂��Ȃ��ė��������Ƃ��Ă��ꋓ�Ɍ��̖��l��̢DEF FN �����̃G�L�X�p�[�g����a�������ł���B�����v���O���}�[�Ƃ��Ă̎��͂͂���Ƃ͓Ɨ��̂��Ƃ���ł���B�V�X�e�����\������\�͂�A���S���Y�����\������\�́A�g�D���Ǘ�����������\�͂Ȃǂ� DEF FN��m��������Ƃ����Ĕ���I�Ɍ��シ���ł͂Ȃ��B�R�[�f�B���O�ɓ������� DEF FN�������C�y�ɁA�ȑO���K�Ɏg����悤�ɂȂ��������ł��邩�甼�l�O�͂�͂�܂����l�O�ł���B��o�̢�X�^�C���u�b�N��͊T�˗ǂ���������Ă��ĎQ�l�ɒl����{����������ł��ł�\�������邪�A���̂Ƃ��A�DEF FN�g�p����l�O�ࣂ����������Ҏ��� DEF FN �ɂ��ĉ��Ə������߂�̂��A���������y���݂ł͂���B��܃t�@�C���c�c�����w��Ȃ�đO�ɁA�\�t�g�̃v������݂���c�d�e�@�e�m�����w��Ȃ�Ă̂��o����Ă���A�v���O���}�[�Ƃ��Ă͔��l�O:�A�}�`���A:��(�ʕ��삪���ł���)�����V�R�V�R�܂Ƃ߂邱�Ƃ͂Ȃ������̂ł���B
�@�Ƃ͂�������ǖ{���́A�c�d�e�@�e�m�����Ƃ����̂́A�v���O�������̐l���������ނ���A��啪��ɂ̓G�L�X�p�[�g�ŁA���̕���ł̏����̂��߂Ƀv���O���������l�����ɂ��������Ă���B���Z�p�҂͌ŗL�Z�p�̏W��ł��鏔���������X�����Ă���̂�����A�ɒl�����ƒ�`��̌����͂�蒼�����Ƃ��Ă���{�I�� DEF FN�������邾���Ţ���x�̋Z�p�I���e�������� DEF FN����������낼��o�Ă���͂��ł���B����������啪��̐l����p���� �c�d�e�@�e�m����ʌ`�ɐ������ė��_�������������e�̔Z�����̂ɂȂ�̂��낤���B�\�t�g���{�E�������悤�ɂ������钘�Ҏ��Ɂu�\�t�g�J����Ƃł͂Ȃ���ʌ�������̂c�d�e �e�m�_�v�����҂��Ă��C�̓łȂ̂�������Ȃ��B�{�e�ł̉��K�ɂ܂�����������A�������Ȃ��� �c�d�e�@�e�m���̂ō��邱�Ƃ͂Ȃ��B
�c�d�e�@�e�m�T���v������C��
�ȏ�̉���ɗp�����v���O��������C�����T�u���[�`���ɂ���[���X�g�T]�Ɏ����B
GOSUB *DEF.FN [[Enter]]
�Ƃ�����ͤ�_�C���N�g����[�h�ł��g�p�ł���̂ŋC�y�Ƀe�X�g���Ē��������B�K�v���������o���ă��i���o�[�������̂��A�X�L�[�Z�[�u����}�[�W�p�̃��C�u�����[���̂��̂ł���B
��j���[�g���̋����@��̗��[���X�g�U]�ɁA�eDEF FN�����̎g�p�T���v����[���X�g�V]�Ɏ����B[���X�g�V]�ł́A�����ւ�'��'�L�[�',,'��܂��͉�ʂ̎w���ɂ��'ESC'�L�[��p����B�O�p�`�̌v�Z�ł͕s�����l�r�����Ȃ��̂�Illegal fanction call�Œ�~����B��U�ł����c�d�e�@�e�m�̂��̌�̎g�p�͎��ɂ������Ȃ��̂��B
�@�Ō�ɁADEF FN���K�����ЂƂB
- �@ �_�o����_�`�a��ʂ钼���ւ��낵�������̑��s�̍��W�����ށB
- �A �Z�o�s�\�̈�̑[�u�ɂ��ďq�ׂ�B
- �B �Z���̎�����ւ��@�́H
- �C �s���`�a�̋�ԓ����ǂ������肹��
- �D �����`�a����_�o�܂ł̋����́H
- �E ��L�̋����ɂ��āA����]�����𐳂Ƃ��镄����t����
�@����A�ǎҏ��Z�쐬�̃��j�[�N�Ȃc�d�e�@�e�m�����쐬�̃��|�[�g�����҂������B
1000 *DEF.FN�@�@�@�@�@�@'�c�d�e�@�e�m������` �T���v�����C��
1100 '�@�@�@�@�@�@�@�@�@save "DEF_FNSM.BAS",A'
1110 '��@�\�ԍ�������̣���y:�Ɨ��ϐ��̂Ȃ�����
1120 '�@���߂ɏ����������̨�����W(GX,GY)
1130 DEF FNGX=POINT(0)
1140 DEF FNGY=POINT(1)
1150 '�@�X�N���[�����W(SX,SY)
1160 DEF FNSX=POINT(2)
1170 DEF FNSY=POINT(3)
1180 '
1190 '
1200 '�@�{���xVAL�@�@�@�@�@�@�� �����_�t���@�@�@�� 0 �t��
1210 DEF FNVALU#(D$)=VAL(D$+FNVALDP$(D$)+STRING$(8,"0"))
1220 DEF FNVALDP$(D$)=STRING$(-(INSTR(D$,".")=0 OR INSTR(D$,"E-")>0),".")
1300 '�@�{���xCDBL
1310 DEF FNCVDBL#(X)=FNVALU#(STR$(X))
1320 '
1400 '�@����������
1410 DEF FNFRC(X)=BRW#*X-FIX(BRW#*X)
1420�@�@�@BRW#=1.00000006#
1430 '
1500 '��_�����̒l��̗��p
1510 '�@�@�傫������I�����锟��
1520 DEF FNMAX(X,Y)=-X*(X>=Y)-Y*(X<Y)
1525 '����������I�����锟��
1530 DEF FNMIN(X,Y)=-X*(X<=Y)-Y*(X>Y)
1540 '
1600 ' X$�������ł��邱�Ƃ̔���
1610 DEF FNNUMS(X$) ="0"<=X$ AND X$
1630 ' X$�������ł��褏����_�̏ꍇ�͕t�������E$���ɏ����_�s���݂̔���
1640 DEF FNNUM(X$,E$)=FNNUMS(X$) OR X$="." AND INSTR(E$,".")=0
1650 '
1700 ' X$���A���t�@�x�b�g�ł��邱�Ƃ̔���
1710 DEF FNALP(X$) =("A"<=X$ AND X$<="Z") OR ("a"<=X$ AND X$<="z")
1720 '
1800 ' X$�����l���A���t�@�x�b�g�ł��锻��
1810 DEF FNALNUM(X$) =FNNUMS(X$) OR FNALP(X$)
1820 '
1900 ' X$��16�i���ł��邱�Ƃ̔���
1910 DEF FNHEXA(X$) ="A"<=X$ AND X$<="F" OR "a"<=X$ AND X$<="f" OR FNNUMS(X$)
1920 '
2000 ' ���l���l��O�ł��邱�Ƃ̔��聩(�����̖��m��)
2010 DEF FNOUTX(X,H,L)=X>H OR L>X
2020 '
2100 ' PC-9801�ż�ķ���������Ă��邱�Ƃ̔���
2110 DEF FNSHIFT=(INP(&HE8) AND &H40)=0
2120 '
2410 PAI#=3.141592653589793#+2.385D-16
2420 RAD#=PAI#/180#
2430 DEG#=180/PAI#
2440 '
2600 '�������/��������
2610 DEF FNACSIN#(X)=-ATN(X/SQR(1#-X*X-(X*X=1)))*(X*X<>1)-SGN(X)*(X*X=1)*PAI#/2
2620 DEF FNACCOS#(X)=-ATN(SQR(1#-X*X)/(X+(X=0)))*(X*X<>0)-(X=0)*PAI#/2
2630 '
2790 '�l��̕ϊ�
2800�@�@ '���ʊp���}�ɕϊ����锟��
2810 DEF FNPNTH#(X#)=X#+2*PAI#*(X#>PAI#)
2820�@�@ '�}����ʊp�ɕϊ����锟��
2830 DEF FNDRC#(X#)=X#-2*PAI#*(X#<0)
2840 '
2890 '�p�x�̉��Z/���Z
2900�@�@'�p�x�̒l�����ʊp(0�`2��:360�x�j�Ƃ�����Z/���Z
2910 DEF FNADDDR#(A#,B#)=A#+B#+2*PAI#*(A#+B#>2*PAI#)
2920 DEF FNSUBDR#(A#,B#)=A#-B#-2*PAI#*(A#
2940 DEF FNADDTH#(A#,B#)=A#+B#+2*PAI#*(A#+B#>PAI#)
2950 DEF FNSUBTH#(A#,B#)=A#-B#-2*PAI#*(B#-A#>PAI#)
2960 '
3000 '�S���ʱ����ݼު��
3010 DEF FNACTN#(X,Y) =FNR0#(X,Y)+FNR1#(X,Y)+(-(X<0)+(X>0)*(Y<0)*2)*PAI#
3020�@�@DEF FNR0#(X,Y) =(.5-(Y<0))*PAI#*(X=0)*(Y<>0)�@�@'X=0:�}90�
3030�@�@DEF FNR1#(X#,Y#)=-ATN(Y#/(X#+(X#=0)))*(X#<>0)�@�@'[ X<>0 ]
3040 'PAI#=3.141592653589793#+2.385D-16'�@�@�@�@(20��)
3050 '
3200 '�������W�̉�]�ϊ�
3210 DEF FNROTX(X,Y,TH)=X*COS(TH)-Y*SIN(TH)
3220 DEF FNROTY(X,Y,TH)=X*SIN(TH)+Y*COS(TH)
3230 '
3490 '�x���b�����x����ݕϊ�
3500 '�@DDD.MMSS �� DDD.DDDD �ϊ�
3510 DEF FNDEG#(X#)=FNDMI(X#)+FNDF1#(X#)+FNDF2#(X#)�@�@�@'DMS$-->DEG
3520�@�@DEF FNDMI(X) =FIX(X*BRW#):BRW#=1.00000006#�@�@�@�@�@'������
3530�@�@DEF FNDF1#(X#)=FIX(FNFRC(X#)*100)/60#
3540�@�@DEF FNDF2#(X#)=FIX((FNFRC(X#)*100-FNDF1#(X#)*60)*100+SGN(X#)/2)/3600#
3550 '
3600 '�@DDD.DDDDDD �� DDD.MMSS �ϊ�
3610 DEF FNDMS#(X#)=FIX(X#)+FNMM#(X#)/100#+FNSS#(X#)/10000#
3620�@�@DEF FNMM#(X#)=FIX(FNFRC(X#)*60)
3630�@�@DEF FNSS#(X#)=FIX((FNFRC(X#)*60-FNMM#(X#))*60+SGN(X#)/2)
3640 '
3990 '�����@��
4000�@�@'��ӂƕВ��p���瑼���p [ B>=A*SIN(TH) ]
4010 DEF FNSINANG(A,B,TH)=FNACSIN#(A*SIN(TH)/B)
4020 '
4050�@�@'��ӂƗ��[���p���瑼�̕�
4060 DEF FNSINLEN(C,TA,TB)=C*SIN(TA)/SIN(PAI#-TA-TB)
4070 '
4090 '�]���@��
4100�@�@ '��ӂƋ��p������
4110 DEF FNCOSLEN(A,B,TH)=SQR(A*A+B*B-2*A*B*COS(TH))
4140�@�@ '�O�ӂ����p������
4150 DEF FNCOSANG(A,B,C)=FNACSIN#(SQR(1-((A*A+B*B-C*C)/A/B/2)^2))
4160 '
4170 '(�]���@��+�����@��)
4180�@�@ '��ӂƂ��̋��p���瑼�̈�p��������
4190 DEF FNTRITH(A,B,TH)=FNSINANG(A,FNCOSLEN(A,B,TH),TH)
4200 '
4210 '�O�ӂ���ʐς����ނP
4220 DEF FNSINC(a,b,c)=sqr(1-((c^2-a^2-b^2)/a/b/2)^2)
4230 DEF FNSQUARE(a,b,c)=a*b*FNSINC(a,b,c)/2
4240 '
4250 '�O�ӂ���ʐς����ނQ�A�w�����̌���
4260 DEF FNS(a,b,c)=(a+b+c)/2
4270 DEF FNSQUAREH(a,b,c)
�@�@�@�@�@�@�@�@=sqr(FNS(a,b,c)*(FNS(a,b,c)-a)*(FNS(a,b,c)-b)*(FNS(a,b,c)-c))
4280 '
4290 '
4300 '���[��/�N�������v�Z
4310 DEF FNLOANX(A,N,R)=-(1-EXP(-N*LOG(1+FNNZ(R))))*A/FNNZ(R)*(R<>0)-N*A*(R=0)
4320 DEF FNLOANA(X,N,R)=-X*FNNZ(R)/(1-EXP(-N*LOG(1+FNNZ(R))))*(R<>0)-X/N*(R=0)
4330 DEF FNLOANN(X,A,R)=LOG(FNNZ(1-R*X/A))/LOG(1+FNNZ(R))*(R>0)-X/A*(R=0)
4350 DEF FNNZ(R)=R-(R=0)
4360 '
5990 '�ėp�c�d�e�@�e�m����
6000 '���l������̕���������苎��
6010 DEF FNNS$(X)=MID$(STR$(X),2)
6020 '���l�̋��w�蕶����Ŗ��߂�
6030 DEF FNSTRB$(X,N,B$) =RIGHT$(STRING$(N,B$)+FNNS$(X),N)
6040 '���l�̋�'0'�Ŗ��߂�
6050 DEF FNSTRZ$(X,N)=FNSTRB$(X,N,"0")
6060 '�����t�ŋ��[���Ŗ��߂�
6070 DEF FNSTRSGN$(X,N)=MID$("+-",1-(X<0),1)+FNSTRZ$(X,N)
6080 '16�i���l�̋�'0'�Ŗ��߂�
6090 DEF FNHEXSTR$(X,N)=RIGHT$(STRING$(N,"0")+HEX$(X),N)
6100 '���������m���ɂ܂�߂锟���͈ȉ��̒ʂ�ł���B
6110 DEF FNRND.$(X#,N)=FNNS$(INT(X#*10#^N+.5)/10#^N)
6120 '���l�̏����w��̔ėp����
6130 DEF FNRDX$(X,N,M)=MID$(FNRDS$(X,N,M),INSTR(FNDP$(X),"."),N-(M>0))
6140�@ DEF FNDP$(X) =MID$(STR$(X),2+(X<0))+STRING$(-(INSTR(STR$(X),".")=0),".")
6150�@�@'(�����_�t�� ������)
6160�@ DEF FNRDS$(X,N,M)=STRING$(N-M+(M=0)," ")+FNDP$(X)+STRING$(M,"0")
6170�@�@'(�����t�� ������)
6180 '
6190 '
7000 '���K�T���v��
7010 '�ꎟ�����͎O�Ɨ��ϐ������I
7020 DEF FNF(X,A,B)=A*X+B'�@�c�c(A<>0)
7030 '
7040 '�����͎l�Ɨ��ϐ������I
7050 DEF FNF2(X,A,B,C)=A*X*X+B*X+C
7060 '
7500 '�k�b���U�̒萔�v�Z
7510�@�@ '���U���g��
7520 DEF FNFRQ(L,C)=1/SQR(L*C)/2/PAI#
7530�@�@ '�����e��CAP
7540 DEF FNCAP(FR,L)=1/4/PAI#/PAI#/FR/FR/L
7550�@�@ '�����C���_�N�^���XLI��
7560 DEF FNLI(FR,C)=1/4/PAI#/PAI#/FR/FR/C
7570 '
8000 RETURN
5000 ' save "NEUTON.BAS",A'�@�@�@�j���[�g���̋����@�̎���
5100 X=1000�@�@'�ؓ��z(����)
5110 A= 120�@�@'�����ԍϊz(����)
5120 N= 10�@�@'�ԍϊ���(����)
5130 '
5140 IF A*N
5210�@�@DEF FNLNX1(A,N,R)=-(1-EXP(-N*LOG(1+FNNZ(R))))*A/FNNZ(R)*(R<>0)
5220�@�@DEF FNLNX0(A,N,R)=-N*A*(R=0)�@�@�@�@�@�@�@�@ 'R=0
5230 DEF FNNZ(R)=R-(R=0)�@�@�@�@�@�@�@�@�@�@�@�@�@�@ '0��1
5240 DLT=.00001�@'�����ψʕ����`
5250 LMT=DLT�@�@ '�덷���E���w��
5260 '
5300�@R=A/X/2�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@'������l
5310 '
5400 *RETRY
5410�@�@D=-2*DLT*(FNLOANX(A,N,R)-X)/(FNLOANX(A,N,R+DLT)-FNLOANX(A,N,R-DLT))
5420�@�@R=R+D
5430 IF ABS(D)>LMT THEN *RETRY�@�@�@�@�@�@�@�@�@�@�@ '�덷�͈͊O�͍Čv�Z
5440 '
5500�@PRINT "��������";USING "###.### [%]";R*100�@�@ '[[��!!]]
5510 END
100 '�@�@save "DEF_FNTS.BAS",A'�@�c�d�e�@�e�m���� ���p�s�d�r�s
110 '�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@1990/07/31,/08/11 T.Mizushima
120 WIDTH 80,25:CONSOLE 0,25,,1:SCREEN 3,0,0,1:COLOR 5,0,0,0,1
130 Q$=CHR$(27):QT$=CHR$(34)
140 GOSUB *DEF.FN 'DEF FN�����̃Z�b�g
150 '
160 PRINT "Please hit Return Key."
170 '
180 WINDOW(0,0)-(1280,800) : LINE(639,0)-( 0,399),7
185 PRINT "(GX,GY)=("FNGX","FNGY"), (SX,SY)=("FNSX","FNSY") ";:INPUT "",X$
190 '
200 X$=" ":PRINT "�{���xVAL/CDBL����"
210 WHILE X$>"":INPUT "Number X$=",X$:X#=VAL(X$)
220�@ PRINT "X$="X$", X#=VAL(X$)="X#", FNVALU#(X$)="FNVALU#(X$);
230�@ PRINT ", CVDBL#(X)="FNCVDBL#(VAL(X$))
240 WEND
250 '
260 X=1.234:PRINT "������:FRAC(X)���� �� MAX & MIN"
270 WHILE X<>0:INPUT " X=",X
280�@ PRINT "FRC(1000*FRC(X))="FNFRC(FNFRC(X)*1000),
290�@ PRINT "MAX(X,PAI#)="FNMAX(X,PAI#);
300�@ PRINT "MIN(X,PAI#)="FNMIN(X,PAI#)
310 WEND
320 '
330 '
340 X$=" " : PRINT "�����͔���:ESC=EXIT"
350 F$="ASC=&&_, Num=##_, Alp=##_, Alp or Num=##_, HEXA=##_, "
360 WHILE X$<>Q$:PRINT " X$=";:X$=INPUT$(1)
370 PRINT USING F$;HEX$(ASC(X$)),FNNUMS(X$),FNALP(X$),FNALNUM(X$),FNHEXA(X$);
375 PRINT USING "Shift=##";FNSHIFT
380 WEND
390 '
400 PRINT "�t�O�p�����ƒl��ϊ�":X=-1
410 WHILE X<>0:INPUT "�}�O�p��X=",X
420�@ PRINT "ARCSIN(X)="FNACSIN#(X)*DEG#,FNDRC#(FNACSIN#(X))*DEG#
430�@ PRINT "ARCCOS(X)="FNACCOS#(X)*DEG#,FNDRC#(FNACCOS#(X))*DEG#
440 WEND
450 '
460 '
470 PRINT "�p�x�̉��Z/���Z:":X=45
480 WHILE X<>0 OR Y<>0:INPUT "�w�}�x:(�w,�x)��",X,Y
490�@ PRINT "(X+Y)="FNADDDR#(X*RAD#,Y*RAD#)*DEG#,FNADDTH#(X*RAD#,Y*RAD#)*DEG#
500�@ PRINT "(X-Y)="FNSUBDR#(X*RAD#,Y*RAD#)*DEG#,FNSUBTH#(X*RAD#,Y*RAD#)*DEG#
510 WEND
520 '
530 '
540 PRINT "�S���ʱ���ݼު��(Y/X)":X=-1
550 WHILE X<>0 OR Y<>0:INPUT "�}���a(X,Y)=",X,Y
560�@ PRINT "ARCTAN(Y/X)="FNACTN#(X,Y)*DEG#,FNPNTH#(FNACTN#(X,Y))*DEG#
570 WEND
580 '
590 PRINT CHR$(12)"���W�̉�]�ϊ� DEMO";
595 X0=320 : Y0=200 : RD= 100 : WINDOW(0,0)-( 639,399)
600 FOR DF =0 TO 1:DRC=1-2*DF
605�@ FOR TH=0 TO PAI#*2-.01 STEP PAI#/12#
610�@�@�@RESTORE 590
615�@�@�@READ X$,Y$ : GOSUB *P.CAL
620�@�@�@PSET(XD,YD) : COL=(RND(TH)*8 MOD 7)+1
625�@�@�@WHILE X$<>"END"
630�@�@�@�@ LINE-(XD,YD),COL
635�@�@�@�@ READ X$,Y$ :GOSUB *P.CAL
640�@�@�@WEND
645�@ NEXT TH
650 NEXT DF
655 X$=INPUT$(1):CLS 3:IF X$<>CHR$(13) THEN 590 ELSE 700
660 DATA 0,+10, 20,+10, 25, 0, 20,-10, 0,-10, 0,+10, END,END
665 '
670 *P.CAL
675�@�@�@XD=X0+RD*(1+DF/2.5)*COS(TH*DRC)+FNROTX(VAL(X$),VAL(Y$),TH*DRC)
680�@�@�@YD=Y0+RD*(1+DF/ 4 )*SIN(TH*DRC)+FNROTY(VAL(X$),VAL(Y$),TH*DRC)
685 RETURN
690 '
700 PRINT "�x���b���x���x���b����ݕϊ�":D=-1
710 WHILE D<>0 : INPUT "�}�x.���b=",D
720�@PRINT "ANGLE="FNDEG#(D)"[Deg], ="FNDMS#(FNDEG#(D))"[DD.MMSS]"
730 WEND
740 '
750 N=10 : B$="*" : M=4 : X=-1
760 PRINT "���l������̉��H:(����="N", ������="M", ���ߕ�����="B$")"
770 F$="No SGN=@_, B$=@_, 00=@_, +0=@_, ": G$="HEXA=@_, Round=@_, Rnd2=@"
780 WHILE X<>0 : INPUT " X=",X
790�@�@PRINT USING F$;FNNS$(X),FNSTRB$(X,N,B$),FNSTRZ$(X,N),FNSTRSGN$(X,N);
800�@�@PRINT USING G$;FNHEXSTR$(FNMIN(X,65535!),4),FNRND.$(X,N),FNRDX$(X,N,M)
810 WEND
820 '
830 PRINT "��ӂƈ꒸�p���p�ƈ��": A=45
840 WHILE A<>0 OR B<>0 :INPUT "(��,��,��B)��",A,B,TH:IF A+B+C=0 THEN 880
850�@�@PRINT "��A="FNSINANG(A,B,TH*RAD#)*DEG#;
860�@�@PRINT ", ��C="180-TH-FNSINANG(A,B,TH*RAD#)*DEG#;
870�@�@PRINT ", ��c="FNCOSLEN(A,B,PAI#-TH*RAD#-FNSINANG(A,B,TH*RAD#))
880 WEND
890 '
900 PRINT "��ӂƓp����ӂƈ꒸�p": TA=45
910 WHILE TA<>0 OR TB<>0 :INPUT "(��,��A,��B)��",C,TA,TB:IF TA+TB=0 THEN 950
920�@�@PRINT "��C="180-TA-TB;
930�@�@PRINT ", ��a="FNSINLEN(C,TA*RAD#,TB*RAD#);
940�@�@PRINT ", ��c="FNSINLEN(C,TB*RAD#,TA*RAD#)
950 WEND
960 '
970 END : GOTO 100
980 '---------------------------
990 '
|
mailto: mizushima00��yahoo.co.jp Last update: 09/01/12 FireFox3�Ή� 06/10/21 �f�ڢThe BASIC���'91/02�`/05�Z�p�]�_�Њ��@���M1990/08/08 |
 (�Q�ƌ�) |
 (�ڎ�) |