関連事項メモ

[三角函数常用公式]

sin(α＋β)＝sinα・cosβ＋cosα・sinβ　………………　(1.　　(加法定理)
sin(α−β)＝sinα・cosβ−cosα・sinβ　………………　(2.
cos(α＋β)＝cosα・cosβ−sinα・sinβ　………………　(3.
cos(α−β)＝cosα・cosβ＋sinα・sinβ　………………　(4.
（(1.＋(2.）／２
sinα・cosβ＝(1/2){sin(α＋β)＋sin(α−β)}　………　(5.
sinα・cosα＝(1/2)sin(2α)　………………………　(5.1
（(3.＋(4.）／２
cosα・cosβ＝(1/2){cos(α＋β)＋cos(α−β)}　………　(6.
(cosα)²＝(1/2){cos(2α)＋１}　……………………　(6.1
（(3.−(4.）／２
sinα・sinβ＝(1/2){cos(α−β)−cos(α＋β)}　………　(7.
(sinα)²＝(1/2){１−cos(2α)}　……………………　(7.1

tan(α＋β)＝[sin(α＋β)]／[cos(α＋β)]
　　　　 ＝(tanα＋tanβ)／(１−tanα・tanβ)　……　(8.1　　(tan加法定理)
tan(α−β)＝[sin(α−β)]／[cos(α−β)]
　　　　 ＝(tanα−tanβ)／(１＋tanα・tanβ)　……　(8.2

(6.1，(7.1のα←α/2 代入
sin(α/2)＝±sqrt{(１−cosα)／2}　 …………………　(9.1　　(半角公式)
cos(α/2)＝±sqrt{(１＋cosα)／2}　 …………………　(9.2
tan(α/2)＝±sqrt{(１−cosα)／(１＋cosα)}
　　　　 ＝±[sqrt{(tanα)²＋１}−１]／[sqrt{(tanα)²＋１}＋１]

sin(2α)＝２sinα・cosα
　　　 ＝２sinα√(１−sin²α)　………………………　(10.1
　　　 ＝２cosα√(１−cos²α)　………………………　(10.2
cos(2α)＝cos²α−sin²α
　　　 ＝１−２sin²α　…………………………………　(11.1
　　　 ＝２cos²α−１　…………………………………　(11.2

sin(α)＝cos(α−π/2)＝cos(π/2−α)
cos(α)＝sin(π/2−α)
tanα＝sinα／cosα
sin²α＋cos²α＝１
sin(−α)＝−sin(α)　…………　奇函数:原点対称
cos(−α)＝cos(α)　……………　偶函数:Ｙ軸対称
tan(−α)＝−tan(α)　…………　奇函数:原点対称

周期函数
sin(α＋２πn)＝sin(α)　…………　
cos(α＋２πn)＝cos(α)　…………　
tan(α＋πn)＝tan(α)　　…………　

sin(α＋π)＝−sin(α)　…………　
cos(α＋π)＝−cos(α)　…………　
tan(α＋π)＝tan(α)　　…………　

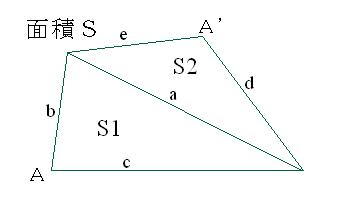
三角形の面積　　　　　　 <SQUARE>

• ２辺とその挟角より：ｂ，ｃ，∠Ａ
  三角形面積Ｓ＝（１／２）ｂ・ｃ・sinＡ
  
  
• １辺とその両端角：ａ，∠Ｂ，∠Ｃ
  算出方針：三角形の内角の和→∠Ａ→正弦定理より他辺長→三角形面積Ｓ
  ∠Ａ＝２∠Ｒ−(∠Ｂ＋∠Ｃ）→sinＡ＝sin(Ｂ＋Ｃ)、
  　ｂ＝ａ／sinＡ×sinＢ＝ａ・sinＢ／sin(Ｂ＋Ｃ)
  ∴Ｓ＝(1/2)ａ・ｂ・sinＣ＝(1/2)ａ²・sinＢ・sinＣ／sin(Ｂ＋Ｃ)
  　　＝(1/2)ａ²／{cosＢ/sinＢ＋cosＣ/sinＣ}
  　　＝(1/2)ａ²／{1/tanＢ＋1/tanＣ}
  
  
• ３辺長ａ，ｂ，ｃの場合　　<SQUARE_3>
  算出方針：円周角一定→第２余弦定理からcos→３平方定理からsin→
  三角形面積Ｓ＝（１／２）ｂ・ｃ・sinＡ により算出
  ａ²＝ｂ²＋ｃ²−２ｂｃ・cosＡ だから、
  cosＡ＝（ｂ²＋ｃ²−ａ²）／（２ｂｃ）
  sinＡ＝sqrt（１−cos²Ａ）
  ∴ Ｓ＝（１／２）ｂ・ｃ・sqrt［１−{(ｂ²＋ｃ²−ａ²)／(２ｂｃ)}²］
  
  
• ３辺長ａ，ｂ，ｃの場合[別解]ヘロンの公式
  　Ｓ＝sqrt{ｓ(ｓ−ａ)(ｓ−ｂ)(ｓ−ｃ)}
  　　　　但しｓ＝(ａ＋ｂ＋ｃ)／２

正矢：半径(弦,正矢) 　　　　　　<Seiya>

　弦長Ｌと正矢ｄから曲率半径Ｒが求められる。
　Ｒ（Ｌ,ｄ）＝｛（Ｌ/２）²＋ｄ²｝／２ｄ
　ｄ（Ｒ,Ｌ）＝Ｒ−sqrt{Ｒ²−(Ｌ/２)²}
See→［正矢計算詳解］
(07/07/21追記)

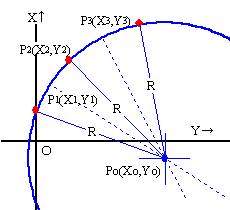
３点を通る円の半径と中心座標　　　<3-Point>

考え方：円の中心は３点から等距離の点。２点から等距離の点は２点を結ぶ線分の垂直２等分線だから、２本の垂直２等分線の交点が円の中心となる。
　　詳細→(３点法試算結果)
　実算出法は、表計算ソフトに布数して中間計算値を順次算出して最終数値を得ると簡単。(07/07/22追記)

[緯度、経度からの座標換算]　 [詳細解説]<Earth>

　　(07/07/23追記)

[マクローリン展開と正弦函数の近似値算出]　　　 <Maclaurin>

Maclaurin's expansion

ｆ(x)＝Ａ₀＋Ａ₁ｘ＋Ａ₂ｘ²＋ Ａ₃ｘ³＋……＋Ａ_nｘⁿ＋……
としたとき、n→∞ でＡ_n→０ に収束する展開をマクローリン展開と云い、近似値算出に用いる。
　係数Ａ_nの算出方法は、ｆ^n・(0)＝n！・Ａ_n で算出。

sinｘのマクローリン展開
ｆ(0)＝sin0＝0＝Ａ₀
ｆ^1・(0)＝　cos(0)＝　１＝１！Ａ₁　　　Ａ₁＝１／(１！)
ｆ^2・(0)＝−sin(0)＝　0＝２！Ａ₂　　　
ｆ^3・(0)＝−cos(0)＝−１＝３！Ａ₃　　　Ａ₃＝−１／(３！)
ｆ^4・(0)＝　sin(0)＝　0＝４！Ａ₄
ｆ^5・(0)＝　cos(0)＝ １＝５！Ａ₅　　　Ａ₅＝１／(５！)
ｆ^6・(0)＝−sin(0)＝　0＝６！Ａ₆
ｆ^7・(0)＝−cos(0)＝−１＝７！Ａ₇　　　Ａ₇＝−１／(７！)
ｆ^8・(0)＝　sin(0)＝　0＝８！Ａ₈
ｆ^9・(0)＝　cos(0)＝ １＝９！Ａ₉　　　Ａ₉＝１／(９！)

ｆ^(2n＋1)・(0)＝(−１)ⁿ＝(2n＋1)！Ａ_(2n＋1)　　　　　(ｎ＝0,1,2,3,……)
　　　　　Ａ_(2n＋1)＝(−１)ⁿ／(2n＋1)！　　Ａ_(2n)＝０

∴sinｘ＝ｘ−ｘ³／3！＋ｘ⁵／5！−ｘ⁷／7！＋ｘ⁹／9！…………

cosｘのマクローリン展開
ｆ(0)＝cos0＝１＝Ａ₀
ｆ^1・(0)＝−sin(0)＝　０＝１！Ａ₁
ｆ^2・(0)＝−cos(0)＝−１＝２！Ａ₂　　　Ａ₂＝−１／(２！)
ｆ^3・(0)＝　sin(0)＝　０＝３！Ａ₃
ｆ^4・(0)＝　cos(0)＝　１＝４！Ａ₄　　　Ａ₄＝１／(４！)
ｆ^5・(0)＝−sin(0)＝　０＝５！Ａ₅
ｆ^6・(0)＝−cos(0)＝−１＝６！Ａ₆　　　Ａ₆＝−１／(６！)
ｆ^7・(0)＝　sin(0)＝　０＝７！Ａ₇
ｆ^8・(0)＝　cos(0)＝　１＝８！Ａ₈　　　Ａ₈＝１／(８！)
ｆ^9・(0)＝−sin(0)＝　０＝９！Ａ₉

ｆ^(2n)・(0)＝(−１)ⁿ＝(2n)！Ａ_(2n)　　　　　(ｎ＝0,1,2,3,……)
　　　　　Ａ_(2n)＝(−１)ⁿ／(2n)！　　Ａ_(2n＋1)＝０

∴cosｘ＝１−ｘ²／2！＋ｘ⁴／4！−ｘ⁶／6！＋ｘ⁸／8！…………

￥１０５．電卓によるsin(x)、cos(x) の近似値計算

sin(x)、cos(x) の転開項値

次 数		sin			cos
		15	85		15	85	度
0		−			1.00000000	1.00000000
1		0.26179939	1.48352986		−
2		−			−0.03426946	−1.10043043
3		−0.00290575	−0.54417380		−
4		−			0.00019573	0.20182452
5		0.00001025	0.05988254		−
6		−			−0.00000045	−0.01480626
7		−0.00000002	−0.00313793		−
8		−			0.00000005	0.00058190	×
9		0.00000000	0.00009592		−		×

　周期２πの函数で、区間０≦ｘ≦π／２ で 函数値０≦f(x)≦１となるグラフ４個で構成されているので、この範囲で何項目まで計算するべきか検討する。(右表)。単位はradだから角度に(π/180)を乗じて換算する。
　有効数字３桁ならsinで５次項、cosで６次項まで算出（計３項）、４桁ならsinで７次項、cosで８次項まで算出（計４項）で足りることが分かる。

sin(x)、cos(x)電卓打鍵法整理(３項近似／４項近似)＋α 　　　　　　<Calc>

sin(x) 布数 key 角度 × 355 ÷ 113 ÷ 180 ×＝ 　 M+ 　 ÷ ５ ÷ ４ − １ × 　 MR 　 ÷ ３ ÷ ２ ＋ １ × 　 MR√ 　 ＝ 　 　 　 　 π≒355／113

cos(x) 布数 key 角度 × 355 ÷ 113 ÷ 180 ×＝ 　 M+ 　 ÷ ６ ÷ ５ − １ × 　 MR 　 ÷ ４ ÷ ３ ＋ １ × 　 MR 　 ÷ ２ − １ ＝±

sin(x) 布数 key 角度 × 355 ÷ 113 ÷ 180 ×＝ 　 M+ 　 ÷ ７ ÷ ６ − １ × 　 MR 　 ÷ ５ ÷ ４ ＋ １ × 　 MR 　 ÷ ３ ÷ ２ − １ × 　 MR√ 　 ＝±

cos(x) 布数 key 角度 × 355 ÷ 113 ÷ 180 ×＝ 　 M+ 　 ÷ ８ ÷ ７ − １ × 　 MR 　 ÷ ６ ÷ ５ ＋ １ × 　 MR 　 ÷ ４ ÷ ３ − １ × 　 MR 　 ÷ ２ ＋ １ ＝

log(x) 布数 key 値x √√√ √√√ √√ ＋ １ ÷＝ ２ ＝− １ × 222.36 ＝± 　 　 　 　 ln(x) 布数 key 値x √√√ √√√ √√ ＋ １ ÷＝ ２ ＝− １ × 512 ＝±

１０x 布数 key 値x ÷ 222.36 ＋ １ ÷＝ ２ ＝− １ ÷＝ ×＝×＝ ×＝×＝ ×＝×＝ ×＝×＝ 　 　 εx 布数 key 値x ÷ 512 ＋ １ ÷＝ ２ ＝− １ ÷＝ ×＝×＝ ×＝×＝ ×＝×＝ ×＝×＝

　関数電卓は現在、某大コンビニチェーンで\980.＋税程度で常備しており、必要時はそれを利用した方が早く確実。\105.電卓での函数算出の実質は「頭のさび落とし」か。出先でどうしても実用的値が欲しい場合の奥の手としてここにｍｅｍｏしておくことにする。
フーリエ級数展開とリップル周波数分析
　

2006/06/18　23:55

---

mail to: adrs				前	主目次
Last Update=06/06/18	06/06/18

---