【整流波形と周波数成分】

　 交流を直流に変換(＝整流)するに際して、直流分（平均値）と共に、阻止すべき変動分の周波数成分が必要である。この分析はフーリエ級数展開に拠るが、波形の位相角から算出する方式と、電気通信など時間軸基準から算出する方法があり、結局は同結果ではあるが、「整流波形」ということから先ず角度基準で算出する。
　 鉄道での実用方式としては、単相全波（２相）整流、三相全波（６相）整流、３相Ｙ−Δ組合せ（１２相）を考えれば足り、３相Ｙ−Δ組合せは、1/2電圧の三相全波整流の位相をπ/６（≡30度）ずらしたものと考えれば３相の変形でピーク値が２種の1/2電圧がπ/6ずれたベクトル和として解析できる。

フーリエ級数基本公式

函数が周期函数の場合：f(x)＝f(x＋2π)：以下の級数で表せる
　 f(x)＝ΣAnsin(ｎx)＋B0＋ΣBncos(ｎx)   ………(1)
　この係数An、Bnを算出するにはsin(ｍx)、或いはcos(ｍx)を乗じて１周期(０〜2π)の間を積分すると、ｍ＝ｎでのみ０以外の値を持て、ｍ≠ｎでは総て０となって、各係数は以下の値となる。
　　Ａn＝(１／π)∫02π f(x)・sin(nx)dx   …………(2)
　　Ｂ0＝(１／２π)∫02π f(x)dx
  …………(3)
　　Ｂn＝(１／π)∫02π f(x)・cos(nx)dx
 		  …………(4)
　更に、Ｙ軸対称(偶函数)であることと、１周期中の繰返し函数の省略演算を利用するなどして計算量を減らせばよい。

［単相全波：２相整流波形］

Ｖ2(x)／Ｖm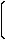＝    sinｘ   ……　0≦ｘ≦π …………(5)
−sinｘ   ……　π≦ｘ≦2π
Ｖ2(x)＝Ｖ2(−x)　：Ｙ軸対称函数
∴正弦項Ａn＝０、直流分と余弦項中の偶数項のみ算出。
∴1/2周期＝0〜πまでの積分値を２倍すれば可
     Ｂ0／Ｖm ＝(１／π)∫0π・sin(x)dx＝２／π ……(直流分)
Ｂn／Ｖm ＝(２／π)∫0π・sin(x)cos(nx)dx
＝(−４／π)Σ｛cos(2mx)／(2m−1)(2m＋1)｝ …m＝1,2,3,4 …∞
∴ Ｖ2(x)＝ (２/π)Ｖm−(４/π)Ｖm[cos(2x)／(1･3) ＋cos(4x)/(3･5) ＋cos(6x)／(5･7)＋
………＋cos(2mx)／{(2m−1)(2m＋1)}＋……]　……(6)
リップル率Ｒ＝交流実効値／直流値＝各周波２乗平均根／直流値　だから、
　 Ｒ＝２･sqrt{(1/1･3√2)2＋(1/3･5√2)2＋(1/5･7√2)2＋(1/7･9√2)2＋……}
　 　＝sqrt{(1/1･3)2＋(1/3･5)2＋(1/5･7)2＋(1/7･9)2＋……}≒0.341651672　……(7)

［３相全波：６相整流波形］

Ｖ6(x)／Ｖm＝  sin(ｘ+π/3)   ……    　0≦ｘ≦π/3 　………(8)
 sin(ｘ)   ……  　π/3≦ｘ≦2π/3
 sin(ｘ−π/3)   ……　2π/3≦ｘ≦3π/3
 sin(ｘ−2π/3)   ……　3π/3≦ｘ≦4π/3
 sin(ｘ−3π/3)   ……　4π/3≦ｘ≦5π/3
 sin(ｘ−4π/3)   ……　5π/3≦ｘ≦6π/3
Ｖ6(x)＝Ｖ6(−x)　：Ｙ軸対称函数(偶函数)
∴正弦項＝０、直流分と、余弦項のみ算出。
Ｖ6(x)＝Ｖ6(x−nπ/3)　 ：π/3毎の繰り返し函数：６周期
∴1/6周期＝π／3までの積分値を６倍すれば可。余弦項は６･ｍ倍のみ。
     Ｂ0／Ｖm ＝{１／(π/3)}∫0π/3・ sin(x＋π/3)dx＝３／π ……(直流分)
Ｂn／Ｖm ＝(６／π)∫0π/3・sin(x)cos(6mx)dx
＝−(６／π)Σ｛cos(6mx)／(6m−1)(6m＋1)｝ …m＝1,2,3,4 …∞
∴ Ｖ6(x)＝ (３/π)Ｖm−(６/π)Ｖm[cos(6x)／(5･7)＋cos(12x)/(11･13)
＋cos(18x)／(17･19)＋cos(24x)／(23･25)＋cos(30x)／(29･31)＋
……＋cos(6mx)／{(6m−1)(6m＋1)}＋…]　……(9)
リップル率Ｒ＝各周波２乗平均根／直流値　だから、
　 Ｒ＝２･sqrt{(1/5･7√2)2＋(1/11･13√2)2＋(1/17･19√2)2＋(1/23･25√2)2＋……}
　 　＝sqrt{(1/5･7)2＋(1/11･13)2＋(1/17･19)2＋(1/23･25)2＋……}≒0.0296593　……(10)

［３相Ｙ−Δ重畳：12相整流波形］

　 １／２電圧で相互にπ/6(＝30度)位相のずれた6相整流波を加算する方式すなわち
Ｖ12(x)／Ｖm＝(1／2Ｖm)｛Ｖ6(x)＋Ｖ6(x−π/6)｝　　　という接続である。
　 先ず位相がπ/6遅れの整流波 Ｖ6(x−π/6)／Ｖm は
周波数成分は基本波の６ｎ倍のみだから、(π／６)×６ｎ＝ｎπで、ｎが偶数だと2πの整数倍で同一極性、奇数だと同一極性2πの整数倍から逆極性となるπだけずれるので、移相しないものと丁度打ち消し合って、偶数次成分のみが残る。
すなわち１２・ｍ倍の周波数のみが残り、６(２ｍ−１)倍の周波数は総て打ち消されて０になることを示す．
Ｖ6(x−π/6)＝ (３/π)Ｖm−(６/π)Ｖm[−cos(6x)／(5･7)＋cos(12x)/(11･13)
−cos(18x)／(17･19)＋cos(24x)／(23･25)−cos(30x)／(29･31)＋
……＋(−1)mcos(6mx)／{(6m−1)(6m＋1)}＋…]　……(10)
{(9)+(10)}／２
∴ Ｖ12(x) ＝(1/2){Ｖ6(x)＋Ｖ6(x−π/6)}
＝ (３/π)Ｖm−(６/π)Ｖm[cos(12x)/(11･13)＋cos(24x)／(23･25)＋
　　……＋cos(12mx)／{(12m−1)(12m＋1)}＋…]　……………(11)
リップル率Ｒ＝各周波２乗平均根／直流値　だから、
　 Ｒ＝２･sqrt{(1/11･13√2)2＋(1/23･25√2)2＋……}
　 　＝sqrt{(1/11･13)2＋(1/23･25)2＋(1/35･37)2＋……}≒0.007260272　……(12)

　 位相差π／６＝30度の１／２Ｖm電圧をそれぞれ全波整流して加算したとした場合の、最大値を求めておく。
一方を基準Ｓとして、もう一方は、
　　　Ｓ･cos(π/6)＋ｊＳ･sin(π/6)＝Ｓ√３／２＋ｊＳ(１／２) だから
この合成値はＶm'＝{(１＋√３／２)＋ｊ(１／２)｝Ｓ、
絶対値｜Ｖm'｜＝sqrt[(１＋√３／２)2＋(１／２)2]･Ｓ
　　　＝sqrt(２＋√３)･Ｓ＝Ｖm・sqrt(２＋√３)／２≒0.965925826
　 この最大値に対し、平均値は　最大値×(12/π)×sin(π/12)
　　　＝(12/π)・(√３−1)／(√8) だから，
元々の最大値Ｖmに対しての平均値は両係数の積になる．すなわち
平均値 ＝Ｖm・sqrt(２＋√３)／２・(12/π)・(√３−1)／(√8)
＝Ｖm・12・sqrt(２＋√３)・(√３−1)／{(２√２)・２・π}
＝Ｖm・３・sqrt{(２＋√３)・(√３−1)2}／(π√２)
＝Ｖm・３・sqrt{(２＋√３)・(４−２√３)}／(π√２)
＝Ｖm・３・sqrt{(２＋√３)・(２−√３)}／π
＝(３／π)･Ｖm　　　となって(11)式と同値である．

［平均値，リップル比較］

　上記計算により各方式の交流最大値に対する平均値と，リップル周波数比，リップルP−P電圧比，リップル実効値電圧比を示す。
  • 　比較対照の単相全波ブリッジは，(最大値を中心に流通角180度：π)
    平均値が最大値×(2/π)・sin(π/2)＝(２／π)≒0.6440、
    リップル周波数比２、
    最大値１に対し最小値がcos(π/2)＝０だから
    　　　　リップルP−P電圧比１。
    　　リップル率≒0.342
  • 　３相６パルス整流（３相ブリッジ結線，２重星形結線）の場合は，(〃流通角60度：π／3)
    平均値が(6/π)・sin(π/6)＝3／π≒0.95493、
    リップル周波数比６，
    最小値がcos(π/6)＝(√3)／2＝0.8660だから
    　　　　P−P値比＝(2−√3)／2≒0.13397。
    　　リップル率≒0.0297
    整流波形
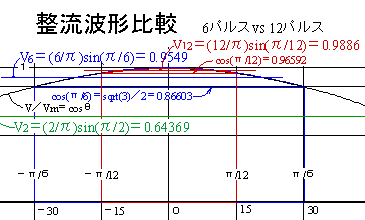
  • 　３相12パルス整流（三相Ｙ−Δブリッジ縦続結線）では，
    （先の計算はＶｍ／２ と、位相がπ/6ずれたもののベクトル和で計算。ここではその合成値をＶｍとしている。結局同値。）
    平均値が(12/π)・sin(π/12)≒0.98861、
    リップル周波数比12，
    最小値がcos(π/12)≒0.96593 だから
    　　P−P値比＝１−cos(π/12)≒0.03407。
    リップル率≒0.00726
  • 　平均値を基準にP−Pと実効値のリップル率を計算すると、12パルス型は６パルス型の１／4.4〜１／4.0909(＝実効値)に下がり、しかもリップル周波数が２倍になって除去し易くなることが分かる。
  • それぞれの整流波形を周波数成分に分けて角周波数ωｔで表すと
    • 単相全波整流
      Ｖ2(t)／Ｖm＝２/π−４/π*{cos(2ωt)/(1*3)＋cos(4ωt)/(3*5)
      　　　　　　＋cos(6ωt)/(5*7)＋cos(8ωt)/(7*9)＋……
      　　　　　　＋cos(2nωt)/((2n−1)*(2n＋1))＋……}
    • ３相全波整流
      Ｖ6(t)／Ｖm＝３/π−６/π*{cos(6ωt)/(5*7)＋cos(12ωt)/(11*13)
      　　　　　　＋cos(18ωt)/(17*19)＋cos(24ωt)/(23*25)＋……
      　　　　　　＋cos(6nω)/((6n−1)*(6n＋1))＋……}
    • ３相全波整流Ｙ−Δ縦続接続
      ピーク値をＶｍとするとき
      Ｖ12(t)／Ｖm＝12/π*sin(π/12)−24/π*sin(π/12)*{
      　　　　　　　 cos(12ωt)/(11*13)＋cos(24ωt)/(23*25)
      　　　　　　＋cos(36ωt)/(35*37)＋cos(48ωt)/(47*49)＋……
      　　　　　　＋cos(12nωt)/((12n−1)*(12n＋1))＋…}
    • 上記３式の初項が直流成分で、第２項以下との比率がリップル率（実効値／直流値）である。平滑度(リップル率)は、周波数により平滑フィルターで大きく変わるので、ナマ波形のリップル率を算出してもあまり意味がなく、下表の様な周波数成分毎の振幅/直流値の方が実際的だろう。２相→６相→１２相と、相数が増えるに従って打ち消されて無くなる周波数成分があることが分かる。
単相全波整流リップル振幅比　周波数成分別ピーク電圧比
ｆ比2f4f6f8f10f12f14f16f18f
2相2/(1*3)
0.66667 		2/(3*5)
0.13333		2/(5*7)

0.05714 		2/(7*9)
0.03175		2/(9*11)
0.02020 		2/(11*13)

0.01399		2/(13*15)
0.01026 		2/(15*17)
0.00784		2/(17*19)

0.00619
6相000000


リップル振幅比　周波数成分別ピーク電圧比
ｆ比6f12f18f24f30f36f42f備考
6相2/(5*7)
0.05714 		2/(11*13)

0.01399		2/(17*19)
0.00619 		2/(23*25)

0.00348		2/(29*31)
0.00222 		2/(35*37)

0.00154 		2/(41*43)
0.00113		３相全波
12相0000Ｙ−Δ縦続


2006/06/30　23:55
mail to: adrs

 旧
旧 		新
新 		戻る
前 		LIST
主目次
Last Update=06/06/30 06/06/30