[260]

BBS
BBS
mail to: adrs
旧
旧 		新
新 		Diary INDEX
Geo日記 		戻る
前 		LIST
主目次

探査機軌道：金星より外か？内か？
今後６年間の軌道：JAXA発表の「図」 vs 「解説」記事

　金星探査機「あけぼの」の軌道投入失敗の記事が９日朝刊各紙に並び、約６年後に再度の軌道投入チャンスがあるとされましたが、後日の発表で原因として燃料の流れが細くなりエンジンが過熱し、縦方向回転を生じて異常発生として緊急待機体制で主エンジン停止とあって、エンジン破損の可能性も強く出てきましたから、今度ばかりは小惑星いとかわ探査機「はやぶさ」の様な薄氷を踏む奇跡的な地球帰還ミッションの様にはいかないかも知れません。

　はやぶさ自体、往路で姿勢制御装置（リアクションホイール）が３軸中２軸故障して必死の裏技でいとかわ接地を成功させており、復路ではさらに推進エンジン全４基の故障に見舞われ、構成要素をつなぎ合わせて１基分を復活させてカプセルのみ帰還という離れ業だったので、機器としての信頼性は高くはないのを、イレギュラーな手動操作でたまたま運良く繋げだということでしょう。

　一旦転けてから裏技で繋ぐのがお定まりの「仕様」なのは彼のNEC-PC「不具合」をなぞったのかも知れませんが、今回ばかりは都合の良い裏技を駆使できない致命的事態の臭いもします。壊れ方が微少であれば、進行方向を軸にスピンを掛けて狂いを平均化して無くしてしまう「はやぶさ」帰還の裏技？を使えるのかどうか？重力が大きく、噴射中に向きを変える必要が有る場合に適切に追従できるかどうかを考えると、益々苦しい事態なのか？とは思いますが、頑張って、何とかピンチ脱出法を編み出して貰いたいと思います。そうでないとまたあの衆愚パフォーマンス反知性派蓮舫議員に問答無用に仕分けられてしまいそうです(ww

　この一連の報道で、相互に矛盾する内容だと思ったのは、今後の金星探査機「あけぼの」の軌道が金星の公転軌道より内側なのか、外側なのかが判然とせず、

内側軌道か？外軌道か？

【ケプラーの法則】　　　<C1>
第1法則（楕円軌道の法則）
惑星は、太陽をひとつの焦点とする楕円軌道上を動く
第2法則（面積速度一定の法則）
惑星と太陽とを結ぶ線分が単位時間に描く面積は一定である（同一軌道で）
第3法則（調和の法則）
惑星の公転周期の2乗は、軌道の長半径の3乗に比例する
(第１、第２法則は中学理科の天文分野)
　この報道事実の何処が相互に矛盾するかといいますと、探査機も金星も動力飛行ではなく、全くの慣性による公転なので、太陽に対して低い・近い軌道ほど高速・短周期で公転、太陽に遠いほど長周期で公転するわけで、日経続報記事の金星10公転に対して探査機11公転で追いつくのが正しいとすれば、探査機の方が平均的には太陽に近い軌道を回っていることになり、JAXA公表図だとする金星軌道の若干外側を追い掛ける図とは相互に矛盾することになります。さてどちらが正しいのでしょうか？

JAXA自体が矛盾資料を配付か？ 　　　<P2>

　資料出所でみますと、次回周回軌道投入可能時期までの今後６年間の略図も、公転数もJAXA発で、情報源の信用性としては同格ですが、金星が10公転、探査機が11公転というのはJAXAが双方の軌道計算の結果から導き出した数値とすれば、10〜11公転もする実際の軌道とは違う只１周の軌道を描いた略図よりは信用できそうに思います。すなわち探査機は金星より内側の軌道で金星を追い掛けていることになります。
　ところが、各紙に載った探査機減速不十分の略図では、探査機が金星の内側を廻る形で接近して、その引力により金星軌道の外側に向けて飛び去っており、金星がほぼ円軌道だとすると、探査機の軌道の長半径の方が金星より長くなる可能性もあります。近日点が極端に太陽に近い軌道のため、金星軌道付近ではその外側を廻っても長半径が金星軌道より短くなるのでしょうか？
　　　　See→ケプラーの第３法則
　この辺の説明が無いままに、矛盾情報が発信されていますが、もう一息、解説を足して貰いたいものです。その辺の矛盾に気付いた社が「図」の掲載を避けたとしたら、掲載した日経夕刊と赤旗新聞は矛盾に気付かなかったことになりますが、それ以前に11周分を１周で描く無理から不採用にし、日経続報のように「金星10周、探査機11周で再投入機会」と書いたのかも知れません。

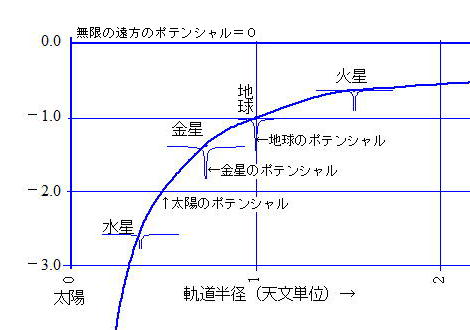ポテンシャル

燃料投下　　　<P3>

　他惑星の観測人工衛星送り込み作業概要を考えるには、重力ポテンシャル＋運動エネルギーで、地球脱出の「第２宇宙速度」以上へ加速して遭遇軌道に乗せることと、他惑星引力圏に突入後、その惑星の第２宇宙速度以下で第１宇宙速度以上への減速を考えれば良いわけで、金星周回軌道への投入は、金星最接近点前後で太陽に対する地球と金星のポテンシャル差分と、地球脱出に際して与えた第２宇宙速度への加速速度ポテンシャル分を逆噴射で打ち消してやる操作だと考えられます。

第○ｎ宇宙速度とは　　　<P4>

ポテンシャル 　ＳＦ好きにはおなじみの第１〜第３宇宙速度というのは、

ケプラーの（第３）法則　　　<P5>

　また、惑星運行に対する経験則として提唱され、ニュートン力学と万有引力の法則として整理されたケプラーの法則でも軌道半径比の問題として試算することができます。鉄道での曲線通過の計算は重力加速度が一定で横Gと半径、カントの関係で済みましたが、惑星間ですと、重力加速度そのものが一定ではなく距離の２乗に反比例なので扱いが面倒になります。
　昔の中学理科天文分野ではケプラーの法則として、
第１法則：楕円軌道の法則　　　＝惑星は、太陽をひとつの焦点とする楕円軌道で公転する
第２法則：面積速度一定の法則＝惑星と太陽とを結ぶ線分が単位時間に描く面積は一定
を、「天体観測結果」として教えていました。

学習参考書により内容が異なる「第３法則」 　　　<P6>

　第３法則は存在自体が全く記憶になく「昔の教科書には無かったはず」と思い近所の本屋で学習参考書を拾い読みすると、ケプラーの第１〜第３法則は中学理科第２分野としては「発展問題＝一部優秀層だけに教える課題」として載っており、高校では物理第２分野と地学に載っています。驚いたのは第３法則の内容が本によって違うこと！
「第３法則：調和の法則：惑星の公転周期の2乗は、軌道の長半径の3乗に比例する」の長半径＝(1/2)長径は同内容ですが、これを「平均半径」とする本と、ご丁寧にも「平均半径（＝長半径）」とする本が有って、無論楕円の平均半径≠長半径ですから学習参考書に重大な間違いが有ることになります。Webサイトでも「長半径」と「平均距離」とに真っ二つですが、その解説には「軌道を円と仮定すれば」となっていて、その場合は長半径＝短半径＝平均距離で違いがないのは当然で、第３法則はそれだけこなれてない内容だということでしょう。

太陽系惑星諸元（2003理科年表p76抜粋）
惑星 軌道半径 周期(年 第３法則
r^3／T^2 		１／ｒ
km天文単位
水　星0.3871 0.2409 0.9995-2.5833
金　星0.7233 0.6152 0.9998-1.3826
地　球1.0000 1.0000 1.0000-1.0000
火　星1.5237 1.8809 0.9999-0.6563
木　星5.2026 11.862 1.0008-0.1922
土　星9.5549 29.458 1.0052-0.1047
天王星19.2148 84.022 1.0049-0.0520
海王星30.1104 164.774 1.0055-0.0332
冥王星39.5404 247.796 1.0068-0.0253

ポテンシャル試算 　　　<P7>

　重心間距離ｒだけ離れた２つの質量Ｍ、ｍ間に働く万有引力Fは、引力定数をＧとするとき、
　　　　Ｆ＝Ｇ（Ｍ・ｍ）／ｒ2
　　ですが、引力のポテンシャルエネルギーとしては、距離無限大∞がゼロで、ｒ地点はそれよりも低位にあり、ｒから∞まで引力Ｆを積分した値が点ｒから見た無限大のポテンシャルエネルギーで、∞の距離を基準「０」にするとＰは負になります。
　　　 −Ｐ ＝∫Ｆdr
＝Ｇ（Ｍ・ｍ）∫r∞（１／ｒ2）dr
　 ＝Ｇ（Ｍ・ｍ）［−１／ｒ］r∞
　 ＝Ｇ（Ｍ・ｍ）｛−１／∞＋１／ｒ｝
　 ＝Ｇ・Ｍ・ｍ／ｒ
　 Ｐ ＝−Ｇ・Ｍ・ｍ／ｒ

　Ｇ、Ｍ、ｍは定数なので、地球軌道半径Ｒを１天文単位（＝太陽−地球間距離）として正規化して比率形状を求めると、
　　　Ｐ・Ｒ／（Ｇ・Ｍ・ｍ） ＝−１／（ｒ／Ｒ） ････ (直角双曲線：上図参照)
　理科年表のデータで「第３法則」の試算をしておきましたが、表の通り良く一致しています。特に火星より内側の岩石型の惑星での一致が目立ちます。ガス型惑星でも誤差0.5%程度です。

　惑星の太陽に対するポテンシャル図と、各惑星周辺のポテンシャル図を重ねてみました。ポテンシャル差以上の初速エネルギーが脱出条件で、各惑星の周回軌道に入るには、その引力圏に到達後、周辺のポテンシャル以下に減速し、しかも第１宇宙速度以上を保つことが条件なのは見てとれます。 　金星探査機を周回軌道に投入するというのは、地球よりポテンシャルの低い金星とのポテンシャル差分は減速した上で、更に減速するということですし、そこから地球に帰還するにはポテンシャル差を登ってくる必要があり、なかなか大変です。小惑星からの帰還は、エネルギー的にはポテンシャル差で戻ってこられるのと比べて、燃料を必要として難しいことが分かります。
　なお地表面付近でのポテンシャル＝位置エネルギーをＭｇＨとしているのは、位置により重力加速度が変わらない範囲だからです。すなわち
　　　　Ｆ＝Ｇ（Ｍ・ｍ）／ｒ2
　　　　　＝ （Ｇ・Ｍ／ｒ2）ｍ
　　　　　≒９．８・ｍ［Ｎ］　･････ 　但し、地表付近で 　(Ｇ・Ｍ／ｒ2)＝９．８［m/s^2］

2010/12/13　02:35
[Page Top↑] 旧
旧 		新
新 		戻る
前