[179]

BBS
BBS
mail to: adrs
旧
旧 		新
新 		Diary INDEX
Geo日記 		戻る
前 		LIST
主目次

変周式受信機の動作は？
　　　回路図では「反結合弛張発振器」に見えるけど？

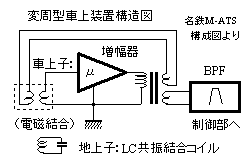
変周式発振回路図

　変周式ATS車上装置の具体的な発振回路が鉄電協テキスト「ATS・ATC」(信号シリーズ7)p18図2-18の「ATS-S形車上装置のつなぎ図」に掲載されていた。右の構成図は名鉄M-ATS資料のものだが、国鉄と同一構成で、このアンプ部は当初のC型車内警報装置では真空管式だったものを、トランシスタ(Tr.)化して更にS型ATSに作り替えたものだ。

　回路図の表記方法はB電源供給が下側になる「真空管回路」方式だ。このトランシスタアンプ(Tr.Amp)の設計者はもろ真空管世代だと分かる(w。Tr.式アンプのS型車内警報装置（＝ATS-Sの原型）が配備された1963年(s38)というとまだPNPゲルマニュームTr.が主流で、翌々年あたりにNECからようやくNPN型のプレーナー型シリコンSi-Tr.2SC182〜185がマイクロディスクTr.として安価に売り出されこれを松下など競合他社も購入使用した頃で、圧倒的にはまだ合金型やドリフト型のゲルマニュームGe-Tr.だった。だからこのAmpがPNPゲルマニウム・トランシスターで構成されるのは当然なのだ。（今はSi.TrやオペアンプICで再設計されている可能性が高いと思うがどうだろうか？工業製品としてのゲルマTr.なんてとっくに存在しない。松下が最後までゲルマTr.を作り続けてSi切替済み各社に逆に供給していた。）
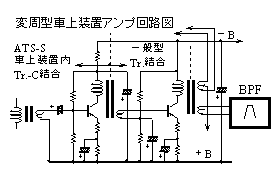
変周式増幅回路図

　増幅段間までトランス結合というのはラジオから拡声器パワーアンプまで初期のTr.AF回路の定番だった。若干意外だったのが、トランス結合回路なのに同時にコンデンサー結合を採用していること(右図左段)。通常はトランス出力はTr.に直結し、巻線の逆極性側でバイアスを供給するものだ(右図右段)。細かな定数が分からないと判断できないが、弛張発振のカットオフ電位をこのＣで作っているのだろうか？もしそうならBE間逆耐圧定格の問題でBにダイオードが必要になるか、選別して逆耐圧の大きい石を使っているのか？増幅度hfe(β)だけでも６層別以上して良品を取っていた時代に更に特別選別なのだろうか？
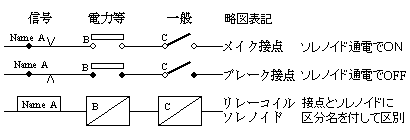　　　　　　リレー回路表記法 リレー回路表記法
　信号方式の記述は「直線」に接点やソレノイドを書き加えるだけの方式なので、多数のリレーを記述するのに楽。電力はC.B.とD.S.など形状で表記を変えたり注記を加えたりで表現している。
　PNP-Tr.の「トランス結合３段」アンプの出力トランスから車上子１次コイルに接続され、２次コイル出力は入力トランスに接続されていて、一見して「反結合発振回路」だ。 車上子の常時(自由)発振周波数での減衰度が50dB、トランシスタ各段はエミッター接地電流饋還型だから、各段20dB弱として60dB弱の利得に車上子での損失-50dBが加わって＋10dB弱となって発振条件となっており、共振型地上子が車上子に電磁結合するとその共振周波数での伝達が増え（＝減衰度が減って）地上子の共振周波数に引き込まれる。
弛張発振波形
　この発振モデルでの問題は、地上子共振周波数に依る通過帯域に変周するというのなら、自励周波数は諸定数の影響で一義的には定まらないからより低い側にも引き込まれる可能性があることだが、変周式の解説を読むと、周波数が上がる方向にのみ変周されるとある。それはマルチバイブレーターなど弛張発振器の特性だ。それはボールを一定の力で打ち上げてそれが落ちてきたところを続けて打つ場合に、地表近くに落ちてくるまではタイミングを制御できず、それは周期を短くする方向しか制御できないのと良く似ている。電子回路で言えばCRT-TVセットの垂直・水平発振に使われる弛張発振器であり、水平・垂直同期で制御できるのは自由発振周波数より周波数を高める方向だけである。これは変周式発振器と同じである。

　回路図を更に読み込むと、B電源や接地電位、供給点などに数箇所の未接続と誤接続があり各増幅段に電源が供給されずこのままでは働かない。PNP-Tr.なのでマイナスアースである車両とは逆電圧で接続の推定が難しい部分がある。AVR出力が電源側と絶縁されて負電源を構成している様だ。
　更に論理部を追うと、時素リレーと思われるUR周辺回路が時素設定できず、アンプ電源も誤接続で供給されず、リレーAR2の電源側片極が(+)に結ばれているが、これも(-)の誤記の模様。あるいは接点AR3はどの制御を受けるのか、ARSはどの接点を駆動するのか(ARS-AR3か？)……p33,35にはATS-ST/-Sw/-SS/-SK結線図があるがI/Oを受けたブラックボックスで「リレー部」、「CPU RYユニット」となっていて受信機外に設置のリレーコイルの片極以外は辿れない。回路図自体に論理構成が表現されるハード論理の表現内容に合わせるにはフローなどの論理図併記が必要だ。確認扱いにブレーキハンドル位置を重なり位置以上にする条件が加わっていることなどは見て取れるが、記載エラーと注記不足が多すぎる。
　この掲載用図面トレース後に設計者か筆者の検図を受けてないのだろう。こういう手抜きは困るが、別添え訂正表に全く載っていないというのは、開発初期の回路図など誰も真剣には読み取らなかったということか。概説なら前出名鉄M-ATS資料図の表記で良いのだろうが、設計・整備側が概要をつかむには具体的回路の方が良いのは勿論である。回路図の読者が少なくても正しく直して貰いたい。バラ部品で構成される-SNの回路図を辿ってみるか。
リレー電磁弁一覧
ATS-Sx機能、概説
−S−SN−ST−Sw
MRSAS
ﾕﾆｯﾄ 		CPU-
ﾘﾚｰ
ﾕﾆｯﾄ		105/103kHz検出、主リレー
−MRPR103kHzMR制御
BR130kHz検出、警報/即停検知
BPR警報/即停BR制御
HCR高減速信号送出検知
CHR高減速車警報
−108.5kHz速照検知
MPR停止警報BR(確認扱)
UR５秒遅延リレー
ACRリセットリレー
AR1B電磁弁&力行制御リレー
AR2受信機接続確認表示
AR3？(ATS主電源投入）
ARS？(主回路AR3？)
SB？(主回路)
BS電磁弁(自動BRK非常制動)
(SNのAR2はPSR1,PSR2）
　　(………と思って-SNの回路図p28図3-5を辿ると、そちらも何かおかしい。構造としては新たに加わった130kHz検出で警報/即時停止を分け、67kHz高減速車信号発信検出HCRで論理を組むのだが、決定的には回路図のままでは５秒遅延停止リレー｢UR｣の遅延機能が-S/-SNどちらも働かないかもしれないのだ。-SN以降では130kHz検出リレーBPRが落ちていると即時停止、上がっていると5秒警報と使い分けるはず。遅延時間が５秒もあると電気屋の感覚ではCを直接使うのが難しくてTr.を使って構成するだろうが、鉄道屋さんはどうやってこの遅延時間を実現したのだろう？コイル部に銅板を巻いて短絡する緩動リレーだと「1号型ATS(1960/12稼動)」に0.8秒と3秒の弁別があり標準的時素0.4秒と1.25秒の遅延リレーが使われているから、時素５秒の遅延リレーはぎりぎり構成可能かもしれない。
　じっと読み込むと、ATS-Sの回路図の電圧安定器AVR出力が＋100Vdc電源とは逆極性の＋接地＝−Ｂ2出力であることの明記がなく、＋接地を前提に見直すと接続ドット●２個を書き落としていて理解の混乱を生んでいる。
　それでも構成を見るとATS-S型はS車内警報装置に５秒タイマー制動論理を加えたというのが分かる。当然であるが105kHzフィルターアンプ出力トランスの短絡線はコンデンサーの誤り。)

　このS型車上装置動作のキーポイントは、常時発振周波数105kHzはBPFをそのまま通り抜けて１石のアンプとダイオードブリッジを介してリレーMRを駆動しており、停止現示地上子に結合して発振周波数が130kHz(123kHz)に変わるとこのリレーMRが落ちて、ベル警報を発し赤色灯を点灯させるものである(ATS-SNでも警報動作する)。推定で修正補足したアンプ部回路図を示しておく。
　絶対停止機能などを付加改良された-Sx型では他の周波数(123kHz & 108.5kHz)のフィルターとリレー駆動回路を増設している。


2008/01/23　02:55
[Page Top↑] 旧
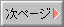旧 		新
新 		戻る
前
ATS-S車上装置回路図
────────────────────────────────────────────────

ATS-Sx車上装置変周式発振回路の解析 　<cal>

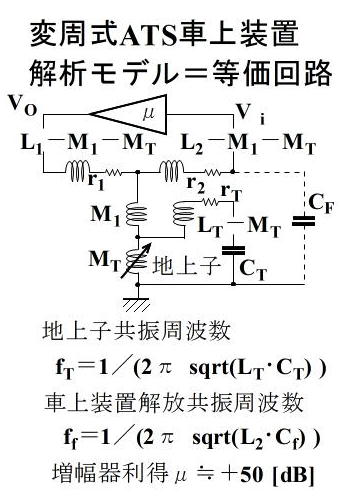ATS-Sｘ等価回路
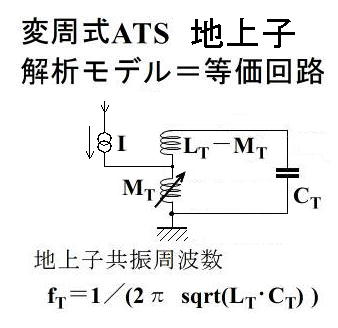地上子簡易等価回路
ATS-Sx変周式地上子簡易等価回路(案)
　ATS-Sx変周式車上装置の等価回路（解析モデル）を、右図のように想定し、
  1. アンプ増幅度μ、アンプ入力電圧≡車上子出力V i、
  2. アンプ出力電圧≡車上子入力電圧Vo、と定め
  3. 車上子駆動コイル定数をL1、r1、
  4. 車上子検出コイル定数をL2、r2、Cf（漂遊容量）、
  5. 車上子入出力コイルの常時の相互誘導をM、車上子入出力コイルと地上子の相互誘導をMt、
  6. 地上子コイルの定数をLt、rt、Ctとして、
  7. 常時発振時は地上子との電磁結合がないからMt＝０、
  8. 車上子・地上子両コイル面が正対した場合のMt>>M、
  9. 常時発振時の利得が約50dBだから、車上子コイルを経ての伝達度がー50dB余、
  10. 地上子コイルのQが、その規格によりQ≧140〜180（＝ωr・Lt/rt ＝1/（ωr・Ct･rt））
    地上子コイルのリアクタンス例：310 [μH]〜355μH 　･･････（「ATS･ATC」p11Lー4、「新幹線信号」ｐ146図3-91鉄電協刊）
  11. 常時発振角周波数ωo（＝２π×103kHz）、地上子共振角周波数ωt、
    地上子共振周波数ｆr＝130〜129.3[kHz]、ATS-Sxで追加＝123、108.5、103、･･････等
  12. 車上子駆動コイル電流 I1
  13. 車上子検出コイル電流 I2
  14. 地上子電流 It
  15. ｓ≡ｊω
といったところが考えられる動作定数である。
車上子コイルの漂遊用量Cfを、受信側・検出側にだけ想定するのは、駆動コイルは低いアンプ出力インピーダンスが効いて、共振ピークがほとんど得られず、検出側なら無負荷で共振の自由振動が得られると考えるからである。
（この想定が崩れると当解析が全く意味を為さない。実物動作で確かめるしかないのが等価回路解析の常である。）
これを、(1)．常時発振時と、(2)．地上子コイル結合時とに分けて、立式して車上子の伝達函数を求めてみる。

(1)．常時発振時　 　<C1>

Vo＝｛ s（L1ーM）＋r 1｝ I1＋｛ s（L2ーM）＋r 2＋1/（s Cf）｝ I2 ･･････････ (1)式
Vo＝｛ s（L1ーM）＋r 1｝ I1＋ s M（ I1ー I2） ･････････････････････････････ (2)式
V i＝｛1/（s Cf）｝ I2 ････････････････････････････････････････････････････ (3)式
　　　以上の３式を満たす I2、V i／Voを求めれば良い。
(2)式を整理すると
Vo＝｛ s L1＋r1｝ I1ーs M I2 　･････････････････････････････････････････････ (2’)式
(1)式、(2')式より I2を求む
Δ ＝ 行列式 s（L1ーM）＋r 1． s（L2ーM）＋r 2＋1/（s Cf） 行列式 ↑
（−１）
↑
s L1＋r 1．ーs M
＝ 行列式 ーs M． s L2＋r 2＋1/（s Cf） 行列式
s L1＋r 1．ーs M
＝ （s M）2ー（s L1＋r 1）｛s L2＋r 2＋1/（s Cf）｝ 　････････････････････ (4)式
Δ I2 ＝ 行列式 s（L1ーM）＋r 1． Vo 行列式
s L1＋r 1．Vo
＝ 行列式 ーs M． ０ 行列式 Vo
s L1＋r 1．１
＝ ーs M Vo 　････････････････････････････････････････････････････････ (5)式
∴ I2＝Δ I2／Δ＝(5)／(4) ＝s M Vo／［（s L1＋r 1）｛s L2＋r 2＋1/（s Cf）｝ ー（s M）2］　･････････ (6)式
∴V i／Vo＝｛1/（s Cf）｝ I2／Vo ＝ M ／Cf［（s L1＋r 1）｛s L2＋r 2＋1/（s Cf）｝ ー（s M）2］　････ (7)式
今、M <;< L1、L2と仮定すると（∵ー50dB≒1/320）、上式(7)は、
∴V i／Vo≒ M ／Cf［（s L1＋r 1）｛s L2＋r 2＋1/（s Cf）｝］ 　･････････････････ (7’)式
ｓ←ｊωo：ｊωo L2＋1/（ｊωo Cf）＝0 で、 ｊωo L2＝ー1/（ｊωo Cf）
ωo＝1/（ L2・ Cf）　･････････････････････････････････････････････････････････ (８)式
ｆo＝1/（ ２π・L2・ Cf）　･･･････････････････････････････････････････････････ (８’)式
と、仮定する。

【 別解 】(3)．地上子コイルが車上子コイルに結合時 　<C3>

　簡易計算法として以下の仮定で伝達特性計算する。
地上子コイルＬが相互誘導Ｍで車上子コイルに結合して、定電流駆動された場合の、誘導電圧Ｖmを算出。すなわち、Vm端から見たインピーダンスＺを求めれば良い。計算に必要な諸定数は
  1. ．地上子コイルＬが相互誘導Ｍで車上子コイルに結合して
  2. ．地上子の共振Ｑ≧140〜180 ･･････････ 「ＡＴＳ・ＡＴＣ」鉄電協刊p
  3. ．Q＝ωoL／r＝１／ωoC r ･･････････ Qの基本定義
  4. ．地上子のＬ≒310 ［μＨ］ ･･････････ 「ATS･ATC」鉄電協刊p11Lー4
  5. ．地上子の共振周波数ｆo＝130 [kHz]、123、108.5、103
  6. ．仮定：ｋ≡M／L ･･････････ （M<<Ｌ、　0≦k<<1）
Z ＝Ｚ1//Ｚ2 ＝Ｚ1＊Ｚ2／（Ｚ1＋Ｚ2） を計算すれば良い。 　･･･････････････････　(1)
Z1 ＝j ω（ＬーＭ）ーj（１/ωＣ）＋ｒ　････････････････････････････････････････　(2)
Z2 ＝j ω Ｍ　･････････････････････････････････････････････････････････････････　(3)
Ｚ1//Ｚ2 ＝j ω Ｍ｛j ω（ＬーＭ）ーj（１/ωＣ）＋ｒ｝／｛j ω Ｌーj（１/ωＣ）＋ｒ｝
＝｛ー ω2（ＬーＭ）＋（1/Ｃ）＋j ω ｒ｝M／｛ｒ＋j（ωＬー１/ωＣ）｝ ･･･（M←kＬ）
＝｛ 1/ωＣー（1ーk）ωL＋j ｒ｝k ωＬ／｛ｒ＋j（ωＬー１/ωＣ）｝ ････････････ （4）
共振点ωo付近で分母が最小！＝Zが最大！、とすれば、
Ｚo ＝｛ー ωo2（1ーk）L＋（１/Ｃ）＋j ω oｒ｝kＬ／ｒ
＝｛ー ωo2（1ーk）L／ｒ＋ （ωo/ωoＣｒ）＋j ωo｝ kＬ
＝k｛ー （1ーk）Q＋Q＋j｝ ωo Ｌ
＝k｛k Q＋j ｝ωoＬ ･･･ 地上子コイルの「共振インピーダンス×Ｑ」の係数2乗倍･･･(5)
ωo＝２π×130[kHz]、L＝310[μH]、Q＝180、としてｋ＝０〜0.1可変とすると
Ｚo ＝0.05｛0.05×180＋j｝（２π×130×1000）×（0.31/1000）
＝1/20（9＋j）（２π×130×0.31）
≒（２π×130×0.31）×sqrt（81＋1）／20≒114　[Ω]

　この相互誘導Mでの電圧降下により車上装置アンプに帰還されて、共振周波数ｆoで発振すると考えられる。
すなわち、アンプ出力電圧VoがL1を介して相互誘導Mに供給されて、地上子共振回路Ztが励振され、そのM端の電圧をL2を介してアンプ入力にV iとして戻して発振させる。 L1もMも誘導性で、電圧位相はほぼそのまま伝わっていると考えられる。

【Zt周波数特性 】描画<C3-2>
　　　ωrＬ/ｒ＝１/ωrＣｒ＝Q　→ｒ＝ωrＬ/Q 　････････････････････････････････････････　(6)
　(4)＆(6)より 　　　｜Z｜＝｜｛ 1/ωＣー（１−ｋ）ωL＋j ωrＬ/Q｝k ωＬ／ ｛ωrＬ/Q＋j（ωＬー１/ωＣ）｝｜　････････　(7)
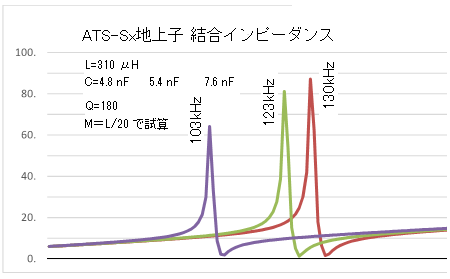
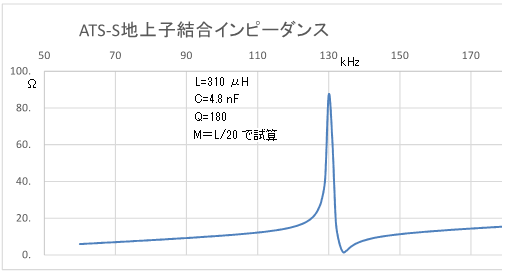ATS-S地上子周波数特性
ATS-S車上装置からみた共振地上子のインピーダンス周波数特性
車上子コイルから高Ｚで励振され、共振周波数に大きなピークと直上に谷
ATS-Sx地上子周波数特性
　以上の条件で(7)式の周波数応答を右図に示す。See→

(2)．地上子コイルが車上子コイルに結合時 　<C2>

地上子コイルが、車上子コイルに電磁結合した場合、M t>>M として、Ｍ＝０とみなして立式（式上は、面倒だからM t←Mで省略表記する）
Vo＝｛ s（L1ーM）＋r 1｝ I1＋｛ s（L2ーM）＋r 2＋1/（s Cf）｝ I2 ･･････････ (1)式
Vo＝｛ s（L1ーM）＋r 1｝ I1＋｛ s（LtーM）＋r t＋1/（s Ct）｝ I3 ･･････････ (2)式
Vo＝｛ s（L1ーM）＋r 1｝ I1＋ s M（ I1ー I2ー I3） ･･････････････････････ (3)式
V i＝｛1/（s Cf）｝ I2 　･･････････････････････････････････････････････ (4)式
　　　以上の4式を満たす I2、V i／Voを求めれば良い。
(3)式を整理すると
Vo＝｛ s L1＋r 1｝ I1ー s M（ I2＋ I3） 　･･････････････････････････････ (3’)式
(1)(2)(3’)式により、I2 を求める
Δ ＝ 行列式 s（L1ーM）＋r 1． s（L2ーM）＋r 2＋1/（s Cf）, ０ 行列式 　　　　↑
s（L1ーM）＋r 1． ０, s（LtーM）＋r t＋1/（s Ct） (ー1、ー１)
s L1＋r 1．ーs M．ーs M ↑　　　↑
＝ 行列式 ーs M． s L2＋r 2＋1/（s Cf）． s M 行列式
ーs M． s M． s Lt＋r t＋1/（s Ct）
s L1＋r 1．ーs M．ーs M
＝ 行列式 s M． s Lt＋r t＋1/（s Ct） 行列式 (ーs M )
−s M． −s M
− 行列式 s L2＋r 2＋1/（s Cf）． s M (ーs M)
−s M． −s M
＋ 行列式 s L2＋r 2＋1/（s Cf）． s M 行列式 (s L1＋r 1)
s M． s Lt＋r t＋1/（s Ct）
＝ −（s M）2｛s（ Lt−M）＋r t＋1/（s Ct）｝
−（s M）2｛s（ L2−M）＋r2＋1/（s Cf）｝
＋(s L1＋r 1)･（s L2＋r 2＋1/（s Cf）） ･（s Lt＋r t＋1/（s Ct）） 　･･･････････････ (5)式

Δ I2 ＝ 行列式 s（L1ーM）＋r 1． Vo, 0 行列式 　　　　↑
s（L1ーM）＋r 1． Vo, s（LtーM）＋r t＋1/（s Ct） (ー1、ー１)
s L1＋r 1． Vo． ーs M ↑　　　↑
＝ 行列式 ーs M． 0． s M 行列式 Vo
ーs M． 0． s Lt＋r t＋1/（s Ct）
s L1＋r 1． １． ーs M
＝ 行列式 1． s M 行列式 (ーs M Vo)
1． s Lt＋r t＋1/（s Ct）
＝ (ーs M Vo)｛ｓ（ Ltー M）＋r t＋1/（s Ct）｝ 　･･･････････････････････････････ (6)式
I2＝(6)式／(5)式、V i＝I2×（１／sCf） より、
V i /Vo＝（M／Cf）×｛ｓ（ Ltー M）＋r t＋1/（s Ct）｝
　　　　　／[（s M）2｛s（ Lt−M）＋r t＋1/（s Ct）｝
　　　　　　＋（s M）2｛s（ L2−M）＋r2＋1/（s Cf）｝
　　　　　　ー(s L1＋r 1)×（s L2＋r 2＋1/（s Cf）） ×｛s Lt＋r t＋1/（s Ct）｝] 　 ･･････････ (7)式
　　　　　＝（M／Cf）×Zt’／｛（s M）2（Zt＋Z2）ーZ1＊Z2＊Zt｝
　　　　　＝Zt’／｛s 2M（Zt＋Z2）ーZ1＊Z2＊Zt／M｝Cf 　･･････････････････････････････ (7’)式
× See↑C3これが、共振周波数ｆt付近で、Zt＝rtだから、
V i /Vo＝r t’／ ｛s 2M（rt＋Z2）ーZ1＊Z2＊rt／M｝Cf の発振となるかどうか！？綺麗には解けない！残念！retry!を期す↑（C３）
　<C3>では、上式 (7’)式中のZtが高いQ（＝140〜180以上）の鋭い共振を示す周波数特性から、その共振点での発振を推定している。

cf.工高電気2年「電気理論2」〜電気3年「電気機械2」参照　　 2017/11/23　26:55