[155]． 日曜毎日誌 長周期地震記事は！

　サンデー毎日4/15号に「大都市・30階以上｣があぶない！｢長周期｣地震動の恐怖p29〜として首都圏の高層ビルが先の能登半島地震で４分以上揺れ続け、中越地震でも同様でエレベータ索綱切断故障などが起こっていることを挙げて家具転倒防止などの被害防止策が必要なことを指摘していた。
　長周期地震問題は、１年半近く前に分布定数型共振の例として超高層ビルの長周期地震波共振破損の可能性として取り上げていて、当HP内単独ページのアクセス数としては信号ATSなど主ページに互してトップグループにいるので、その記事にひとこと言いたくなった。このほか電鉄の整流方式というのも同様に上位にあるが、あれは頭のサビ落としでフーリエ級数解析を思い出すために整流波形と周波数成分を算出したもの。アクセス実績は意外な内容がヒットし、狙ったものは飛ばずで思うようにはいかないものである。

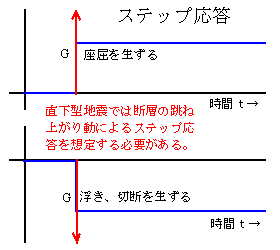
　記事で欠けている視点は、振動加速度Ｇで見るべきところを振幅でみていること。初期の超高層ビルが共振周期を長くして関東大震災型(海洋型)振動の破損回避を図るだけで、振動吸収や長周期振動対応が考慮されていないこと、建物自体の共振特性・振動吸収機能には触れず、そして直下地震のステップ波衝撃は建築設計が全く考慮していないことが挙げられる。

　振幅を言う場合揺れ振幅の安全範囲が周期に比例して大きくなることを無視しては恐怖を煽るだけになってしまう。エレベータ鋼索が構造物に当たって損傷するのは相互に振動周期が異なって衝突するからで、振れ止めが不十分ということで、地震振動が殺人的ということではない。

　記事では平野の軟弱地盤の振幅増大作用と共振周期には触れているが、建物に鋭い共振点があれば振動が数倍以上に増幅されることには触れてない。共振すると振動１周期毎に振幅が大きくなり振動減衰と平衡するまで増大する。仮に振動の定振幅Ａで、進行波・反射波１往復して再反射される効率をαとして、ｎ回反射を繰り返した場合の単純加算の全振幅Ｗを計算し、ｎ→∞の極値を算出すれば、以下の通り無限級数の和として求められる。

振動反射率と
増倍度

反射率 α	増倍度 W∞/A
0.5	２
0.6667	３
0.75	４
0.8	５
0.9	１０
0.95	２０

W	＝A(１＋α＋α2＋α3＋α4＋α5＋……＋α(n-1)＋αn)
方程式両辺にαを乗じて
Wα	＝A(　　α＋α2＋α3＋α4＋α5＋α6＋…　……＋αn＋α(n+1))
前式から後式を引くと最前項と最後項を残して他項は消去され、
W(1−α)	＝A(1−α(n+1))
W	＝A(1−α(n+1))／(1−α)　　　となるが、
ｎ→∞ の極値を求めると、０≦α＜１ だから αn →０
W∞	＝A／(1−α)
(W∞／A)	＝1／(1−α)＝Ｑ　　　（振動増倍率Ｑ）

減衰率α毎の増倍度は右表の通りとなる。
　すなわち、一往復の反射率αの値により数倍〜10倍の振幅に増倍されることが分かる。逆に言えば連続振動型(≒海洋型)地震であれば往復の吸収率を大きく（反射率を小さく）すれば破損を抑えることができる。高層ビルで言えば振動吸収の制振装置がこれに当たる。振動による水流の抵抗で振動エネルギーを吸収するものが多い。この詳細を超高層ビル毎に公表すると、古いビルほど怖い状況が出てくるのではないだろうか。関東大震災の振動波形のみでシミュレーションをして建設したとされる霞ヶ関ビルは、その通りなら当時の地震計では長周期振動を拾えなかったから無防備ということになる。後日、振動を吸収する制振装置を追加しているだろうか？従前「耐震設計」と云っているのは強度を上げてＧに耐えるものを言い、共振周波数をズラして波動伝播中に振動エネルギーを吸収しようとする試みとは違うアプローチである。超高層ビルの旧設計では柔構造で共振周波数を低くしてはいるが、振動吸収機構が無いことで長周期地震被害のリスクを非常に高めている心配があるのだ。

　また「キラーパルス」の定義が釈然としない。
　周期１秒前後の振動が日本家屋に最も被害を与えることから、計測震度の定義でもその付近の振動数に最大の重みを付けたフィルターを定義している。これを「キラーパルス」と言うのだろうか？→（全壊が際だって多かった中越沖地震の震源近くでの振動波形に、周期１．３秒の強い揺れが1分余に渉って続くのがみられ、これが木造家屋倒壊に大きく影響した模様＝キラーパルス）
　この「キラーパルス」という言葉は直下型地震である阪神淡路大震災で使われるようになって、震源断層直近の一瞬のステップ衝撃による激しい破壊動を言ったはずで、その結果、高層ビルの特殊鋼の主柱が切断されるなどインパルス負荷が想定される直下型地震特有のステップ応答型振動を指すもので、一撃の最大Ｇで潰れたり、逆に建造物が一瞬宙に浮いたりして激しく破壊されるものを指し、震度定義の対象である連続波的な海洋型地震とは違うと思っていたが、記事にはそうした区別は全くない。能登半島地震被害の様に屋根の質量が破損に効いたとか、断層のステップ振幅そのものが破壊に直結するのだろう。

　記事としては「長周期振動」に触れただけで、深い突っ込みはなく、怖いぞ怖いぞだけではチトお手軽に過ぎる気がする。

旧

新