�k�x�|�����x�̐���
�@ �k�x�̊��ϑ��̎���(1978�N�K�蓙)�A���ȔN�\�ɂ͊T�˂̐U�������x���L�ڂ���Ă����B�������Ȃ��猚���̋��U���g���Ŕ�Q���قȂ邽�߁A�U�����g���ɑ���t�B���^�[�������`����K�v���������B1991�N�K��ł͌v���k�x���������ꂽ���A�k�x�V�����͔�Q��������̔F��Ƃ��Ďc��A�܂��U�������x�\�L���Ȃ��Ȃ����B 1996�N�ɂ͑��Čv���k�x�Ƃ��A�k�x�T�`�U�����ꂼ�ꋭ��ɕ����āA���̃t�B���^�[���������肳��Ă��邪�A�k�x�̉����x�\�L�͕������Ă��Ȃ��B�@ �������A���肳�ꂽ�t�B���^�[�����}�ł́A���Ƃ��Ɣj��͂̋����P�b�����������P�Ƃ���Ă���A���ꂪ����Ǝv����̂ŁA1978�N������Q�l�Ɏ��Z���Ă݂�B
�@ 1996�N�k�x��͂܂��u�v���k�x�v�𑪒肵�A������l�̌ܓ��Łu�k�x�v�Ƃ��邪�A�k�x�T�`�U�ɂ��Ă͋�����Q������A�Ƃ������̂�����A�k�x�O�Ɛk�x�P�̋��E�ƂȂ�v���k�x���O�D�T�ƂȂ�B�������̊����E�F0.8cm/s^2�ł���A�k�x�O�D�T���I�t�Z�b�g�ƂȂ�B
cm/s2��gal��10-2m/s2�B �����E�����x��78�N��Ɋ�Â����� (�k�x�V��'96�N�A�v���k�x�ƂȂ� ��91�N����Ōv���k�x�v���������ꂽ���k�x�V�͔�Q�����ŔF�肳��A�ڈ��̉����x�����L�ڂƂȂ����B����܂ł�78�N��ł͉����x���Q�l�l�Ƃ��ċL�ڂ���k�x�V�͊T��400gal�`�Ƃ���Ă���) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
�@ ���̒�`�ł����Ə]�O�͐k�x�V�̋��E�F400cm/s^2�����͗B��̗�O�ŁA����Ƃ��Ă�800cm/s^2�ł���ׂ��������B����͍ŐV���X�U�N����Ɛk�x�U����450�`800cm/s^2�����N�Ɛ��肳���800cm/s^2�ȉ��̐k�x�V���P�^�Q�����N���̐k�x�U���ɂȂ��Ă���B
�@ ���z�n�k�ő����̉Ɖ��|�����Ȃ���A�k�x�Ƃ��Ă��V�ł͂Ȃ��A�U���ɗ��܂����̂͂��̊�ύX�̂��߂Ƃ͍l�����Ȃ����낤���H
| �y�U�������x�|�k�x��`�̐���z04/11/06�L |
�k�x�V�F
�@ �C�ے��̐k�x�K���ōł������h��B�h��̂��߂Ɏ����̈ӎv�ōs�����邱�Ƃ��ł��Ȃ��Ȃ�܂��B�����ł́A�قƂ�ǂ̉Ƌ�傫���ړ����A��Ԃ��̂�����܂��B�ϐk���̍���������Z��ł��A�X������A�傫���j��������̂�����܂��B�傫�Ȓn�����n���ׂ�A�R���ꂪ�������A�n�`���ς�邱�Ƃ�����܂��B�ȑO�́A�k�x�V�͌����̓|��Ȃǂ��猈�߂��Ă��܂������A�X�U�N����k�x�v�Ō��߂���悤�ɂȂ�܂����B�@ �k�x�́A�X�P�N�܂ł͋C�ے��E�����̊��Ȃǂɂ�茈�肵�Ă��܂������A�X�P�N�S������k�x�v���g�����ϑ��ɕς��܂����B
�@ ���̌�A�X�U�N�P�O���ɁA����܂Ők�x�O����k�x�V�܂ł̂W�i�K�������k�x�K�����A�k�x�T�Ɛk�x�U�Łu���v�u��v�Q�i�K���ɂ����P�O�i�K�ɕύX���܂����B
�@ ��_��k�Ђ̐k�x�V�́A��Q������ɔF�肳��܂����B���z�n�k�ł̐k�x�V�́A�k�x�v�ŏ��߂ċL�^����܂����B
�Ԋ��V��04/10/31���j�P�ʉ��
�@ �k�x��`����@�@�i�C�ے��k�x�j�@�@<teigi>
�@ �k�x��`�͑��̑̊������w�W�Ɠ������@�ł̒�`���l�ƃI�t�Z�b�g�O�D�T�łقڈ�v����B���Ȃ킿�U�������x�̂ʼn����x�ϑ��l�������l�Ŋ����āA���̃G�l���M�[���10���Ƃ���ΐ����u�v���k�x�v�Ƃ��邪�A�̊��ŏ����E�Ƃ����(0.8[cm/s^2])���v���k�x�O�D�T�ƂȂ�l����l�Ƃ���B���̂��ߑ��̕����ʂ̉���U���̒�`�ɔ�ׂO�D�T�i���T���a�j�̃I�t�Z�b�g����B�@ �u�k�x�ɂ��ẮA�v���k�x�����������l�̌ܓ�����B����͐�グ������A��̂đ������v�Ƃ������Ƃł���B�u�G�l���M�[��v�Ƃ������Ƃ́A�����x��͂Q�悳��ΐ��l�ł͂Q�{�ƂȂ�B���Ȃ킿
| �v���k�x�� | �Q�ELOG(�U�������xcm/s^2�^��lcm/s^2)�@�@ ����{���ɂȂ邩�� | ||||||||||
| �O�D�T�� | �Q�ELOG(�O�D�Wcm/s^2�^��l | cm/s^2) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| �P�O^(1/4)�� | 1.7783��(�O�D�W�^��l) | ���i�P�O^(1/4) �́A�P�O�̂S�捪�j | |||||||||
| ��l�� | 0.44987[cm/s^2]�@�@�@�]���� | ||||||||||
| �v���k�x�� | �Q�ELOG(�U�������x[cm/s^2]�^0.44987�j
| �U�������x��
| 0.44987�E�P�O^(
�v���k�x�^�Q�j[cm/s^2]�@�@�@(��s�̋t�ϊ�)
| �k�x��
| Int�i�v���k�x�{0.5)
| ��(�v���k�x�̎l�̌ܓ���)�@�@�ƂȂ�B
| ��
| Int�o�Q�ELOG(
�U�������x�^0.8�j}�@��Int�i�j�͐��������i�������؎́j
| | |||
�@ �������Ȃ���A����ł͐k�x�V�̊���]�O�ɔ���Q�{�ɂ��傫���Ȃ�̂ŁA���n��I��r�ɂ͋���Ƃ̕��L���K�v�ɂȂ�B����͔�Q��Ȃǐ���ɒ��������˂Ȃ��̂ŏڍׂȉ���t���Ŏ��m�����ׂ��ł���B
| �t�B���^�[ | �@�@�@�@�@�@�Z�@�@�@�@�� | |
|---|---|---|
| ���@�� | sqrt(1/f) | |
| �n�C�J�b�g | 1�^sqrt{�P�{0.694y^2�{0.241y^4�{0.0557y^6�{ �@�@ 0.009664y^8�{0.00134y^10�{0.000155y^12} | |
| ���[�J�b�g | sqrt[�P�|{�P�^exp(2f)^3}] | |
�@ �k�x�U�`�V�͓]�|�E����E�f�w�ړ��Ƃ�������������Q������鋫�E�̂��ߎЉ�I�ɍׂ��ȋ敪��v�������͖̂������Ȃ����A����͕����X�P�[����c�Ȃ���̂ł͂Ȃ��A�ו������ď����_�敪��݂��ĉ������ׂ��ł���B�k�x�T�`�U��������Q�������̂��P�i�K��10�{�ł͔�Q�̗l�����傫���Ⴂ������̂łQ���������̂��낤�B�i�����`�����̉��ƐU���A�d���g���x�ł����a��p���ċ��x�i�K��10�������Ă���B�j����ɂ��k�x�P�K��������3.16�{�A�O�D�T�K����1.778�{�̉����x�ƂȂ�B �@ ���͋C�ɂ����˂��ăX�P�[�����Ȃ���̂͐k�x���ʂ��蓾�Ȃ�������̂ŋ؈Ⴂ���B���Ƃ��Ɛk�x�V�͕���n�k(1948/6)�̌��r��Q�������ĕt��������ꂽ�k�x�K��������A���̕����ʂƂ��Ă̐����Ɏ�̔N����v�������c�݂��c��̂��낤���B
04/11/09�@23:00�L
�@ ���ۓI�k�x�@���������J���k�x�K�@1931�N����i�⑫�j<kokusai>
| �ٶؐk�x | �v�Z�l | ���l | ||||
|---|---|---|---|---|---|---|
| �k �x | �����x | �����x | ||||
| �ŏ� | �ő� | �ŏ� | �ő� | |||
| �O | �| | �| | ��0.43 | |||
| �T | �| | ��1.0 | 0.43�� | ��0.93 | ||
| �U | 1.0�� | ��2.1 | 0.93�� | ��2.0 | ||
| �V | 2.1�� | ��5.0 | 2.0�� | ��4.3 | ||
| �W | 5.0�� | ��10.0 | 4.3�� | ��9.3 | ||
| �X | 10�� | ��21 | 9.3�� | ��20 | ||
| �Y | 21�� | ��44 | 20�� | ��43.2 | ||
| �Z | 44�� | ��94 | 43.2�� | ��93.1 | ||
| �[ | 94�� | ��202 | 93.1�� | ��201 | ||
| �\ | 202�� | ��432 | 201�� | ��432 | ||
| �] | 432�� | �� | 432�� | 931�� | ����` ��` | |
| 11 | �� | �� | ��931 | 2005�� | ||
| 12 | �� | �| | ��2005 | 4320�� | ||
�@ �C�ے��k�x�͓��{�����̓K�p�ł���A���O���ł�1931�N����̉����u�����J���k�x�K�v���p�����Ă���B
�@ �����x�̎Q�l�l����́A���̐k�x�̊�l���A�ǂ������Ȃ��B���l�̌������킹������ƁA�k�x�R�i�K���ɉ����x��10�{�̑ΐ��X�P�[���ɂȂ��Ă���̂ŁA�k�x�]�̉���432gal�ŃX�P�[�����킹���������̂����\�ł���B
�@ ���Ȃ킿�A��l0.201gal�Ƃ̔�̏�p�ΐ������A10�{�̉����x�i100�{�̃G�l���M�[�j�����R�k�x�i�K�Ƃ������́F���Ȃ킿�����x���p�ΐ��l���R�{�ɂقڈ�v����B
�@ �����ł͒n�k�̕p�x���������s�s��ł̕���n�k�̗l�Ȍo�������Ȃ��������A�C�ے��k�x�K�V������400gal�ɑ������郁���J���k�x�]��432gal�ȏ�͌��r��Q�ōו������ꂽ���߁A�����x�͖���`�Ń��j�A�[�X�P�[���ł͂Ȃ��̂��낤�B�k�x�P�D�T���ɃG�l���M�[���P�O�{�Ƃ�����`�@�͓Ɠ��ő��ɗ���݂Ȃ��B��p�Ȃ��P�O���Q�A�����_��͂ł͎��R�ΐ��̒������낤�B���̓_�ł͐U���E���ȂǑ��̕����ʔ�r��ł����P�O��̑ΐ�����Ƃ����C�ے��k�x�K�̑Ó��������邱�ƂɂȂ�B
| �ٶؐk�x�� | �R�ELOG(�U�������xcm/s^2�^��lcm/s^2)�@�@ | ||
| �k�x�]������ | 432gal�Ƃ���� | ||
|---|---|---|---|
| ��l�� | �O�D�Q�O�P[cm/s^2]�@�@�@�]���� | ||
| �ٶؐk�x�� | Int�o�R�ELOG�i�U�������x�^�O�D�Q�O�P�j�p | Int�o �p�@�͐�̂Ĕ��� | |
| �U�������x�� | �O�D�Q�O�P�~�P�O^(�ٶؐk�x�^�R�j [cm/s^2] | (��s�̋t�ϊ�) | |
04/11/21�@17:00�L
�@ ��������U�����x���Z�@�@<shindo>
�@ �n�k�̗h������X�e�b�v���C���p���X��ł͕ʂ̕��͌v�Z���K�v�����A���ɐ����g�̌J��Ԃ��U�����f��(���C�m��n�k���f��)���l����Έȉ��̊T�Z���o����B| �U�������x�� | ���ő�����x�`�Esin(�p���g���ց~������)�@�ł���Ƃ� | ||||||||
| �U�����x�� | ���烿 dt���|(�`/��)�Ecos(�ցE��)�{�萔�b
| �U�������@
| ���炖 dt���|(�`/��^2)�Esin(�ցE��)�{�b�E��
| �U�����g��f
| ���P�g���A�ő�����x800cm/s^2�@�Ƃ���Ƃ��A
| �ց��Q�~
| ���g�������Q��������
| �ő�U�����`�^��^2
| ���W(m/s^2)�^(�Q��)^2��0.2026���A�h�ꕝ�łQ�{��0.4053���I
| |
�@ �� ���Y�斱���̕��v�|������11/08�[���g�b�v�Ɍf�ڂ���Ă��邪�A�Ă̒�n�Ղ���u�Ŕ�яオ���ĕ���o����E������X�e�b�v�����̗l�����B���ꂾ�ƒE���������ɖ߂���������ւƌ����ׂ����B�E�����̃t�����W�����P�c��̂͂��̌�̒E���Ȃ̂�������Ȃ��B
2004/11/08�@00:50�L
�������n�k��聁���U�Ɛ������@<cho_shu_ki>
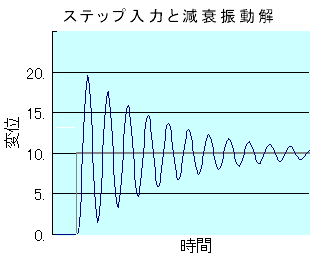 �@ ��ʓI�ȓ��{�̌����ł͌����̌ŗL�U���������P�b�O��Ƃ���A�n�k�g�̎���������ɍ����Ƒ傫�Ȕ�Q�ɂȂ�B�C�ے��u�v���k�x�v�̃t�B���^�[����(��o)�͂���ɍ��킹�Ē�`�������̂��낤�B���̓��{�̌����ɑ���C�m�^�n�k�̑O��ł́A�f�w�̒��ˏオ��f�ڎ钼���^�n�k�̃X�e�b�v�����Ƃ͋������o�邵�A�����w�r���̂悤�ɏ_�\���ɂ��ċ��U��������ɒ������̂ɂ��āu�֓���k�Ћ��̒n�k�ɂ��j��������v�����ꍇ�́A�z��O�̒�������(���U���g����)�n�k�Ɍ�����ꂽ�ꍇ�A�h�ꂪ�傫����������Ĕj��Ɏ��錜�O������B���قɌ����u�����w�̖閾���v�ƌ���ꂽ�����փr���̑ϐk���@�������`�ʂ�_�\���ɂ��ċ��U�_���g�����P�g�����y���ɒႢ�l�ɂ��Ă��邾���ŐU���z���@�\(���k�@�\)���Ȃ��Ƃ���ƁA���̋��U���g���̒�������U���n�k�g�Ɍ�����ꂽ�ꍇ�ɐ��E�f�ՃZ���^�[�r��������݂̑�S���ɂȂ肩�˂Ȃ��Ƃ������Ƃ��B���U���ۂŐU���͐��{�`���S�{�ɂȂ邱�Ƃ�����B
�@ ��ʓI�ȓ��{�̌����ł͌����̌ŗL�U���������P�b�O��Ƃ���A�n�k�g�̎���������ɍ����Ƒ傫�Ȕ�Q�ɂȂ�B�C�ے��u�v���k�x�v�̃t�B���^�[����(��o)�͂���ɍ��킹�Ē�`�������̂��낤�B���̓��{�̌����ɑ���C�m�^�n�k�̑O��ł́A�f�w�̒��ˏオ��f�ڎ钼���^�n�k�̃X�e�b�v�����Ƃ͋������o�邵�A�����w�r���̂悤�ɏ_�\���ɂ��ċ��U��������ɒ������̂ɂ��āu�֓���k�Ћ��̒n�k�ɂ��j��������v�����ꍇ�́A�z��O�̒�������(���U���g����)�n�k�Ɍ�����ꂽ�ꍇ�A�h�ꂪ�傫����������Ĕj��Ɏ��錜�O������B���قɌ����u�����w�̖閾���v�ƌ���ꂽ�����փr���̑ϐk���@�������`�ʂ�_�\���ɂ��ċ��U�_���g�����P�g�����y���ɒႢ�l�ɂ��Ă��邾���ŐU���z���@�\(���k�@�\)���Ȃ��Ƃ���ƁA���̋��U���g���̒�������U���n�k�g�Ɍ�����ꂽ�ꍇ�ɐ��E�f�ՃZ���^�[�r��������݂̑�S���ɂȂ肩�˂Ȃ��Ƃ������Ƃ��B���U���ۂŐU���͐��{�`���S�{�ɂȂ邱�Ƃ�����B�@ �ŋߒ������n�k�����݂��邱�Ƃ�������A�K�����݂܂Œ����w�̐Ǝ㐫��������n�k�͋N���Ă��Ȃ����A���̔j��̌��O���u�������n�k����v�Ƃ����B
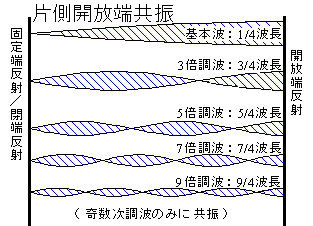 �@ �U����͓I�ɂ����A�ȈՂɏW���萔�ōl����Ύ��ʂƒ�R�ƃo�l�萔�ŋ��U���g��(���P�^���U����)�ƌ����萔�����܂��ŁA���݂̒����w���z�ł͎��g���͂��炷���\���̓�����R�ɂ�錸���萔�����܂�ӎ����Ă��Ȃ�����A�v�l�̋��U���g���̒������n�k�g�ɑς����邩�ǂ����ۏႪ�Ȃ��̂��B���\���̏ꍇ�K�ȓ�����R����������̂���ϓ���A�n�k�g�̂f�ɑ��鍄���𑝂��u�ϐk�v�v�Ő蔲���Ă��邪�A�����_�I�ɂ͋��U�̋����̐��䂪�\�Ȃ�A������őϐk���𑝂����Ƃ��\�ł���B�E�̐}�͕Б��J���[�̕��z�萔�^���U�F�`���H�^���U�̐}�����A�`���H�ɓK�ȋz���v�f�������ƍ����g�ł̋��U���N���蓾�邩�狤�U���������邾���̑ϐk�Ή��ł͕s�\���ȏꍇ���N���蓾��B�����փr���v���̊�Ƃ����֓���k�Ђ̐U���g�`�̒��S���g�����PHz�Ƃ��āA�͋[�����������r�����g�̊�{���U���g����啝�ɒႭ�v�������Ƃ͒m���Ă��邩��A�V���A�X���A11�����c�c�����g���U�ɑ��Ă͈ꉞ�̐U������������������Ȃ̂��낤���A�����͖��m�������������n�k�̊�{�g�A�R���U���ϗ͖͂��m���ł���B
�@ �U����͓I�ɂ����A�ȈՂɏW���萔�ōl����Ύ��ʂƒ�R�ƃo�l�萔�ŋ��U���g��(���P�^���U����)�ƌ����萔�����܂��ŁA���݂̒����w���z�ł͎��g���͂��炷���\���̓�����R�ɂ�錸���萔�����܂�ӎ����Ă��Ȃ�����A�v�l�̋��U���g���̒������n�k�g�ɑς����邩�ǂ����ۏႪ�Ȃ��̂��B���\���̏ꍇ�K�ȓ�����R����������̂���ϓ���A�n�k�g�̂f�ɑ��鍄���𑝂��u�ϐk�v�v�Ő蔲���Ă��邪�A�����_�I�ɂ͋��U�̋����̐��䂪�\�Ȃ�A������őϐk���𑝂����Ƃ��\�ł���B�E�̐}�͕Б��J���[�̕��z�萔�^���U�F�`���H�^���U�̐}�����A�`���H�ɓK�ȋz���v�f�������ƍ����g�ł̋��U���N���蓾�邩�狤�U���������邾���̑ϐk�Ή��ł͕s�\���ȏꍇ���N���蓾��B�����փr���v���̊�Ƃ����֓���k�Ђ̐U���g�`�̒��S���g�����PHz�Ƃ��āA�͋[�����������r�����g�̊�{���U���g����啝�ɒႭ�v�������Ƃ͒m���Ă��邩��A�V���A�X���A11�����c�c�����g���U�ɑ��Ă͈ꉞ�̐U������������������Ȃ̂��낤���A�����͖��m�������������n�k�̊�{�g�A�R���U���ϗ͖͂��m���ł���B�@ �����w�r���̐U���͊y��̌��U����͂̂悤�����z�萔�^�i���i�s�g�{���˔g�̏d��j�Ƃ��ĉ�͂���̂��K�Ǝv�����A���̔��˓_�i��b�F�Œ�[�Ɛ�[�F����[�j�߂��ɑ��x���̓�����R�v�f��t�����邱�ƂŐU�����z�����邱�Ƃ͉\������A�d�v�Ȍ����ۑ�ɂȂ�B����ɐݒu�̐��k���^���N�͊J���[�ł̐U���G�l���M�[�z���̎��݂̈�ƌ��邱�Ƃ��ł���B
�@ �U���g�͊�b�Ɖ�����������āA���̈ʑ����d�Ȃ���u���z�萔���U�v�ƂȂ��đ傫�ȕΘ߂ɂȂ茚����j��B(�В[����U���������{���U�g���͈�l�������̖�S�{�ŁA���U���g���͊�{���g���̊�{�ƂȂ�B�g�����x�͌����ŗL�̒萔�ɂȂ�j�B�������r���ɐU���z���@�\���L��Δ��˂̉����Ō������邩��ʑ�����v���Ă������U�����������ł���B
�m�⑫�n�@�����փr���ɂ��g�ݍ��܂�Ă����U���z���@�\
�@�����փr���ɂ��U���z���@�\���g�ݍ��܂�Ă��邱�Ƃ��������B�Z�����g�`�݂̂̊֓���k�Ђ̐U���g�`�Őv�E���������Ƃ͎��������A���k�ނƂ��ėv���Ɂu�X���b�g�ǁv��z���āA���ꂪ�n�k���Ŕj������Ɩ߂�̍R�͂������Ȃ�A�����̐U����~�ς��Ȃ��B���Ȃ킿�X���b�g�ǂ��n�k���ŏ��X�ɕ���Ă���Ԃ́A���U�������オ��Ȃ��ōςނ��A�X���b�g�Ǖ����S�����Ă��܂��ƐU�����z���ł��Ȃ��Ȃ�B�r���̎������̑�k�ЂɂP��͑ς���l�����ł��邪�A���ĕ��ꂽ��̂Q�x�ڂ̐��k�͂Ȃ��B�@���݂̐U���z���@�\�Ƃ��ẮA�~���_�ȏ�̉Y���̈�̑傫���S�ނ�n�k���ɂ��ό`�����邱�ƂŐU���G�l���M�[���z��������������̗p����Ă���B�~���_�����̕ό`�ł͒e���̈�ɗ��܂�A�U���͋z�����Ȃ��ő傫���Ȃ邪�A�~���_����Y���ό`�̈�ɒB����Ɛ��k�@�\�Ƃ��ē��삷��B(2011/04/11�NjL)
2005/12/20�@00:10�L
���U�͖��������̘a�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@<Q>
���U����ƐU���P�������ɐU�����傫���Ȃ�U�������ƕ��t����܂ő��傷��B���ɐU���̒�U���`�ŁA�i�s�g�E���˔g�P�������čĔ��˂������������Ƃ��āA���˂��J��Ԃ����ꍇ�̒P�����Z�̑S�U���v���v�Z���A�������̋ɒl���Z�o����A�ȉ��̒ʂ薳�������̘a�Ƃ��ċ��߂���B| ���˗� �� | ���{�x W��/A
| 0.5 | �Q
| 0.6667 | �R
| 0.75 | �S
| 0.8 | �T
| 0.9 | �P�O
| 0.95 | �Q�O
|
| |
|---|
| �@W | ��A(�P�{���{��2�{��3�{��4�{��5�{�c�c�{��(n-1)�{��n) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
���������ӂɃ����悶��
|
�@W�� | ��A(�@�@���{��2�{��3�{��4
�{��5�{��6�{�c | �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�c�c�{��n�{��(n+1))
�O������㎮�������ƍőO���ƍŌ㍀���c���đ����͏�������A
|
W(1�|��) | ��A(1�|��(n+1)) |
W | ��A(1�|��(n+1))�^(1�|��)�@�@�@�ƂȂ邪�A |
������ �̋ɒl�����߂�ƁA�O�������P ������ ��n ���O |
W�� | ��A�^(1�|��) |
(W���^A) | ��1�^(1�|��)�@�@�@�i�U�����{���F�p�j | | |||
�@���Ȃ킿�A�ꉝ���̔��˗����̒l�ɂ�萔�{�`10�{�̐U���ɑ��{����邱�Ƃ�������B�i���{�x�ɂ��ẮA���U��H�ł��p�ŕ\���Ă������A�l�����͓��l�ł���B�j
�@�t�Ɍ����Ή����̋z������傫���i���˗����������j����Δj����}���邱�Ƃ��ł���B���w�r���Ō����ΐU���z���̐��U���u������ɓ�����B�����ɂ͐U���ɂ�鐅���̒�R�ŐU���G�l���M�[���z��������̂������������A���U�_�����点�����k�q������A��~���_�|���g���đY���ό`�ŐU���G�l���M�[���z��������������̗p����Ă���B
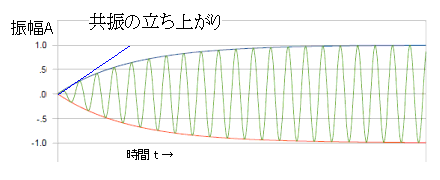
�@�]�O�u�ϐk�v�v�Ɖ]���Ă���̂͋��x���グ�Ăf�ɑς�����̂������A���U���g�����Y�����Ĕg���`�d���ɐU���G�l���M�[���z�����悤�Ƃ��鎎�݂Ƃ͈Ⴄ�A�v���[�`�ł���B�����w�r���̋��v�ł͏_�\���ŋ��U���g����Ⴍ���Ă͂��邪�A�U���z���@�\���������ƂŒ������n�k��Q�̃��X�N����ɍ��߂Ă���S�z������̂��B
2007/04/12�@23:55�L
�����n�k�̓X�e�b�v������͗v�@�@�@�@�@�@�@�@�@�@�@<Step>
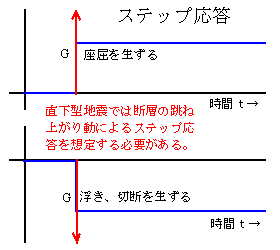 �@�����w�r���ł̒������U�����ƕ���Ŗ��𖾂ȐU�����A�����^�n�k�f�w���ӂŐ���(�W��)���ς��X�e�b�v�����̉𖾂��B��_�W�H��k�Ђł͒f�w�����ߕБ��ɏW�����ē|�Ă���ꏊ�������A�����w�Z��̓S���̎和���j�f���Ă����Ƃ��̑z������Q�������A�u�L���[�p���X�v�̑��݂��w�E���ꂽ���A���̐��̂͒n�Ղ̒��ˏオ��A�@���t���̉\��������B���k�p���X�ƐL���p���X�Ƃǂ��炪�j��I�Ȃ̂��낤�B���s�̌��������g��֓���k�Њϑ��g�ɂ��V�~�����[�V���������ł͑���Ȃ��B�X�e�b�v�����̑Ō��ɐU���������傫�Ȕj��ɓ���B
�@�����w�r���ł̒������U�����ƕ���Ŗ��𖾂ȐU�����A�����^�n�k�f�w���ӂŐ���(�W��)���ς��X�e�b�v�����̉𖾂��B��_�W�H��k�Ђł͒f�w�����ߕБ��ɏW�����ē|�Ă���ꏊ�������A�����w�Z��̓S���̎和���j�f���Ă����Ƃ��̑z������Q�������A�u�L���[�p���X�v�̑��݂��w�E���ꂽ���A���̐��̂͒n�Ղ̒��ˏオ��A�@���t���̉\��������B���k�p���X�ƐL���p���X�Ƃǂ��炪�j��I�Ȃ̂��낤�B���s�̌��������g��֓���k�Њϑ��g�ɂ��V�~�����[�V���������ł͑���Ȃ��B�X�e�b�v�����̑Ō��ɐU���������傫�Ȕj��ɓ���B�@�u�C�m�^�n�k�v�Ɖ]���Ă��������f�w�̒���͒����^�n�k�ł���A���������܂��܊C���Ȃ����B�����^�Ɖ]���ǂ��k�����痣���ɏ]���ĊC�m�^�Ƃ̈Ⴂ�͂Ȃ��Ȃ�͂��B�n�k�g�̑��x���T��P�g��7km/s�O��AS�g��4km/s�Ƃ���Ă���A�k���[����10km��Ƃ����̂�S�g�̐��g����������A�t�ɒ���̒n�ʂ���̔��ˁF�n�ʎ��ʂ��g���F�U�����g���ɉe�����ĉE�}�̂悤�Ȍ����U���ƂȂ�͈͂��u�����^�v�Ȃ̂�������Ȃ��B�\�����ꂽ�n�_�̒n���͂��ꂼ��̐U�����g���̌����x�̈Ⴂ�ɂ͂Ȃ��Ă��U�����g�����̂��̂�ς��邱�Ƃ͂Ȃ��B
[[�S��ˏo�̒��z���n�k�̓X�e�b�v�����^��?]]�@�@�@See��<Killer>
 �@�����U���̎��g���͊O������^������̂ł͂Ȃ��A�W���萔�n���f���ł͎��ʂƃo�l�萔�i�Q�K�������̌W���ƒ�W�����j�ɂ���Č��܂�B�n�Ղɓ����X�e�b�v�ψʂ��^�����Ă��A���x�ƍ����Ŏ��g�����傫���ς��B���ʂ͑傫������Ղ̂悤�ȋ����������Ȃ����n�͌ŗL�U�����g���������遁�ŗL�U�������������Ȃ邾�낤���A������������������ǂ�Ȍ��ʂɂȂ�̂��낤�H�O����`����Ă����U���̎��g�����ς��킯�ł͂Ȃ��B |
�@�ؑ��Ɖ��̋��U���g�����PHz�O��Ƃ����̂��v���k�x�v�̃t�B���^�[�����Ƃ��č̂������Ă��邪���U�Ƃ����̂͌J��Ԃ��U�����O�B���g���h���C���ł̉�͂ł̓X�e�b�v�����^�Ō��̔j��͗ǂ������Ȃ����낤�B���̒n�k�g�`�Ă݂����B
�@TV�ł͂PHz�O��̘A���U�����u�L���[�p���X�v���Ɖ�����Ă��邪�A�Ɖ��̉������݂�A�k�����߂̒n�\�ɒi���������悤�Ȑ��������̃X�e�b�v���������u�L���[�p���X�v�ƌĂԂɂӂ��킵���n�Ղ̓����Ō����U���������A�k�����痣���ɏ]���Ċg�U�E�������ČJ��Ԃ��U�����x�z�I�ɂȂ�̂ł͂Ȃ����B
| ���� | ��10:13:29 |
| �쐼 | ��10:13:31.5 |
| ���� | ��10:13:31.5 |
| �q | ��10:13:34 |
| ���� | ��10:13:36.5 |
| ������ | ��10:13:38.5 |
�@�ƁA�v���Ĉȉ��̒n�k�g�T�C�g�߂�ƁA���܂��܉Ɖ�����̑�������n��̔g�`���Ȃ��A�܂邫�蕪����Ȃ����A�B��A�R�N�O�̒��z�n�k�̐k���n�ł���R�Îu���̐U�����x�f�[�^�ŁAXYZ�̐����������P�f���ő�Ƃ����������v���l���I�����^�k���t�ߓ��L�̌��ۂ������ĂȂ��B�����̋��x���炵�ď㉺�����U���Ɛ��������U���ł͔j����E���Ⴂ�������B����̊ϑ��f�[�^���̂͂���悤�Ȃ̂ŁA�g�`�Ƃ��Č��J�����̂�҂������B
�@�@�@�m�R�Îu�F��k524gal, ����722gal, ���㉺1059gal ����1132gal�n
�@http://www.hinet.bosai.go.jp/topics/common/low/?TOPICS_CF=niigata070716
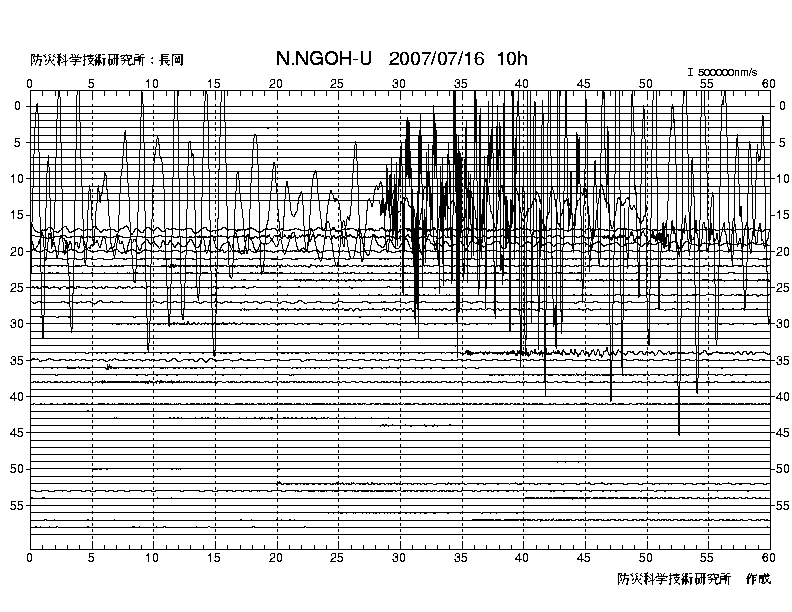
�@�L�^�}�͂P���P���Ԃʼn������Ԏ������P���A������c��60�{���ׂĂP���ԕ���\���Ă��邩��o�g�̓��B��0.5�b���x�̕���\�œǂ݂Ƃ�邪�A�n�k�v���̂��̂̎��g�������F�X�e�b�v����������Ȃ��̂Œf�w�X�e�b�v�������邩�ǂ����c�c�c�B�Q�����ɓn�范�����h��Ă���B�r�g�̐U���ϒ������ɖ�20�b���݂��邩��G����͗ǂ�������Ȃ���20�b�Ƃ����������U��������̂�������Ȃ��B����e�e�s��͂ŏo�Ă��邾�낤�B�֓���k�Дg�`�ł͒����������L�^�ł��Ȃ���������A���̔g�`�ŊJ�����������w�r���Œ������n�k��肪�N���Ă���BS�g�̓��B�����ɂ͓ǂ݂Ƃ�Ȃ����A��R�b�]��̑傫�ȗh�ꂾ�낤���H5.5�b�ゾ�낤���H �@�@�@�@(07/07/17�NjL)
�������I�L���[�p���X�H�@�@�@<Killer>
�@�n�k�g�`���悭�悭����A������1.3�b�̑傫�Ȓn�k�������ɑ�z���ĂQ���O�㑱���Ă���̂�������B���̎����͓��{�Ɖ��̌ŗL�U�������ł͂Ȃ����B�X�e�b�v���������ɒ��ڂ��Ă��ċC�t���Ȃ��������A���̐U�����������ԑ����̂Ȃ狤�U���Ĕj���Ɏ����Ă������͂Ȃ��B���U�����̐U�����ٗl�ɒ��������U�����������猚���̓|�����ɒ[�ɍ����̂��낤�B���ꂪ�L���[�p���X�̐��̂ł͂Ȃ����낤���H �@�@�@�@(09/02/11�NjL)
2007/04/16�@23:55�L
|
mail to:
| 
|

|

|
| |||
| Last Update��2007/07/17�@�@�@ (07/04/16,/12,05/12/20�C04/11/21�C/10�C/08�C/06 | |||||||