新京成電鉄津田沼-
新津田沼間曲線標識
総武線鉄橋手前Sカーブ
 津田沼-新津田沼-前原間は144Rだらけ。津田沼、R右2直角、R左直角、総武交差、R左直角、新津田沼、R右直角………という感じ!転向角が大きいためか計測精度も良い.
津田沼-新津田沼-前原間は144Rだらけ。津田沼、R右2直角、R左直角、総武交差、R左直角、新津田沼、R右直角………という感じ!転向角が大きいためか計測精度も良い.
【「考え方」であり、
3点を通る円の中心座標と半径の質問リンクから当ページに来られた皆さん! |
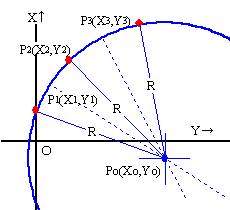 勾配α1=-(x2-x1)/(y2-y1)
……………………………………… (2)
勾配α1=-(x2-x1)/(y2-y1)
……………………………………… (2)| (α2-α1)x | =
+α2・xm2
-α1・xm1-ym2+ym1 |
|---|---|
| ∴ x0 | =
{+α2・xm2
-α1・xm1-ym2+ym1}
/(α2-α1) …(7) |
| y0 | = α1(x0-xm1)+ym1 ……………………………………(8) |
| ∴ R | = sqrt{(x1-x0)2 +(y1-y0)2} …………………(9) |
| or R | = sqrt{(x2-x0)2 +(y2-y0)2} CHK-1 |
| or R | = sqrt{(x3-x0)2 +(y3-y0)2} CHK-2 3値同値でok! |
 津田沼-新津田沼-前原間は144Rだらけ。津田沼、R右2直角、R左直角、総武交差、R左直角、新津田沼、R右直角………という感じ!転向角が大きいためか計測精度も良い.
津田沼-新津田沼-前原間は144Rだらけ。津田沼、R右2直角、R左直角、総武交差、R左直角、新津田沼、R右直角………という感じ!転向角が大きいためか計測精度も良い.
|
| 2(x3-x2), | 2(y3-y2) | * | x0 | = | x32-x22+y32-y22 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2(x2-x1), | 2(y2-y1) | y0 | x22-x12+y22-y12 | ……(4),(5) |
| 1-1, | 1-2 | ≡(1-1)×(2-2)-(2-1)×(1-2) ………(行列式の定義) | ||
|---|---|---|---|---|
| 2-1, | 2-2 |
| Δ= | 2(x3-x2), | 2(y3-y2) | |
|---|---|---|---|
| 2(x2-x1), | 2(y2-y1) | ……………………(6) |
| Δx0= | x32-x22+y32-y22, | 2(y3-y2) | |
|---|---|---|---|
| x22-x12+y22-y12, | 2(y2-y1) | ………(7) |
| Δy0= | 2(x3-x2), | x32-x22+y32-y22 | |
|---|---|---|---|
| 2(x2-x1), | x22-x12+y22-y12 | ………(8) |

|
| 緯度X | 経度Y | 垂直2等分線 | 半径 R | 公称 R | 誤差 % | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 度 | 分 | 秒 | 度Deg. | 度 | 分 | 秒 | 度Deg. | 勾配α | ( Xm,Ym ) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 新京成 津田沼 | P1 | 35 | 41 | 3.66 | 35.684350 | 140 | 1 | 24.66 | 140.023517 | 基準点 | 0 | 0 | 142.936 | 144 | -0.7
| P2
| 35 | 41
| 8.66 | 35.685739
| 140 | 1
| 20.81
| 140.022447
| 5.919084
| 77.162
| -13.036
| 142.936
| P3
| 35 | 41
| 11.30 | 35.686472
| 140 | 1
| 21.85 | 140.023517
| -0.844239
| 195.067
| 22.186
| 142.936
| 97.088 | 104.904
| ※京成津田沼出発直後、切り通しの単線右カーブ144Rで約180゜曲がる部分。
|
| 京王調布 | 相模原線 P1
|
| 35 | 39
| 6.55 | 35.651819
|
| 139 | 32
| 26.85 | 139.540792
|
| 基準点
| 0
| 0
|
| 159.457
| 173
| -7.8
| P2
| 35 | 39
| 8.00 | 35.652222
| 139 | 32
| 28.88
| 139.541356
| 5-0.879043
| 22.377
| 25.456
| 159.457
| P3
| 35 | 39
| 8.61 | 35.652392
| 139 | 32
| 31.18 | 139.541994
| -0.326395
| 54.168
| 79.754
| 159.457
| -94.649 | 128.327
| ※京王相模原線調布出発後左へ90゜曲がる173R部分の引き込み線含む3線部。
|
| 代々木 | 南東 P1
|
| 35 | 40
| 53.11 | 35.681419
|
| 139 | 42
| 19.47 | 139.705408
|
| 基準点
| 0
| 0
|
| 297.405
| 300
| -0.9
| P2
| 35 | 40
| 54.48 | 35.681800
| 139 | 42
| 14.15
| 139.703931
| 0.317036
| 21.143
| -66.688
| 297.405
| P3
| 35 | 40
| 56.22 | 35.682283
| 139 | 42
| 11.54 | 139.703206
| 0.820758
| 69.138
| -166.093
| 297.405
| 296.686
| 20.669
| ※中央線千駄ヶ谷-代々木間の盛り土複々線右カーブ
|
| 飯田橋
| P1
|
| 35 | 42
| 4.91 | 35.701364
|
| 139 | 44
| 40.86 | 139.744683
|
| 基準点
| 0
| 0
|
| 326.026
| 300
| 8.7
| P2
| 35 | 42
| 7.36 | 35.702044
| 139 | 44
| 44.5
| 139.745694
| -0.828845
| 37.810
| 45.617
| 326.026
| P3
| 35 | 42
| 08.60 | 35.702389
| 139 | 44
| 49.05 | 139.746958
| -0.335602
| 94.755
| 148.255
| 326.026
| -209.024
| 250.204
| ※中央線飯田橋駅の盛り土複々線+引き込み線跡+島式ホーム左カーブ
|
| 神田- | 万世橋間 P1
|
| 35 | 41
| 47.97 | 35.696658
|
| 139 | 46
| 14.89 | 139.770803
|
| 基準点
| 0
| 0
|
| 294.787
| 300
| -1.7
| P2
| 35 | 41
| 44.74 | 35.695761
| 139 | 46
| 17.29
| 139.771469
| 1.657181
| -49.847
| 30.079
| 294.787
| P3
| 35 | 41
| 42.30 | 35.695083
| 139 | 46
| 17.94 | 139.771650
| 4.622054
| -137.349
| 68.306
| 294.787
| -199.150
| -217.344
| ※中央線神田-旧万世橋駅間の左カーブ
|
| 瀬野- | 八本松1 P1
|
| 34 | 26
| 2.67 | 34.434075
|
| 132 | 38
| 54.71 | 132.648531
|
| 基準点
| 0
| 0
|
| 308.885
| 300
| 3.0
| P2
| 34 | 26
| 6.50 | 34.435139
| 132 | 39
| 2.33
| 132.650647
| -0.609410
| 59.106
| 96.990
| 308.885
| P3
| 34 | 26
| 12.35 | 34.436764
| 132 | 39
| 4.78 | 132.651328
| -2.895240
| 208.493
| 225.161
| 308.885
| 304.392
| -52.490
| ※山陽線瀬野-八本松駅間の急勾配カーブ
|
| 瀬野- | 八本松2 P1
|
| 34 | 26
| 43.33 | 34.445369
|
| 132 | 39
| 35.66 | 132.659906
|
| 基準点
| 0
| 0
|
| 298.155
| 300
| -0.6
| P2
| 34 | 26
| 39.76 | 34.444378
| 132 | 39
| 31.58
| 132.658772
| -1.061029
| -55.094
| -51.925
| 298.155
| P3
| 34 | 26
| 38.41 | 34.444003
| 132 | 39
| 27.19 | 132.657553
| -0.372891
| -131.022
| -159.721
| 298.155
| 142.699
| -261.789
| ※山陽線瀬野-八本松駅間の急勾配カーブ
|
| 姫川- | 駒ヶ岳 P1
|
| 42 | 4
| 39.92 | 42.077756
|
| 140 | 36
| 25.54 | 140.607094
|
| 基準点
| 0
| 0
|
| 300.472
| 300
| 0.2
| P2
| 42 | 4
| 40.92 | 42.078033
| 140 | 36
| 39.65
| 140.611014
| -0.095484
| 15.432
| 161.623
| 300.472
| P3
| 42 | 4
| 25.86 | 42.073850
| 140 | 36
| 43.52 | 140.612089
| 5.242167
| -201.548
| 367.582
| 300.472
| -236.253
| 185.655
| ※函館本線姫川-駒ヶ岳間180度カーブ(付近で3回の過速度転覆事故)
|
| 尼崎事故
| P1
|
| 34 | 44
| 31.89 | 34.742192
|
| 135 | 25
| 35.82 | 135.426617
|
| 基準点
| 0
| 0
|
| 284.547
| 302
| -5.8
| P2
| 34 | 44
| 28.35 | 34.741208
| 135 | 25
| 35.01
| 135.426392
| -5.318502
| -54.631
| -10.272
| 284.547
| P3
| 34 | 44
| 26.56 | 34.740711
| 135 | 25
| 33.84 | 135.426067
| -1.861794
| -136.886
| -35.381
| 284.547
| -3.064
| -284.530
| ※塚口-尼崎間上り右302R第一カーブ。建物の影の影響
|
| 横田基地 | 北西 P1
|
| 35 | 45
| 52.80 | 35.764667
|
| 139 | 20
| 28.41 | 139.341225
|
| 基準点
| 0
| 0
|
| 408.849
| 400
| 2.2
| P2
| 35 | 45
| 58.22 | 35.766172
| 139 | 20
| 30.45
| 139.341792
| -3.274351
| 83.644
| 25.545
| 408.849
| P3
| 35 | 46
| 03.41 | 35.767614
| 139 | 20
| 36.98 | 139.343606
| -0.979537
| 247.383
| 132.858
| 408.849
| -33.011
| 407.514
|
| 横田基地 | 北西 再計算 P1
|
| 35 | 45
| 52.91 | 35.764697
|
| 139 | 20
| 28.37 | 139.341214
|
| 基準点
| 0
| 0
|
| 391.569
| 400
| -2.1
| P2
| 35 | 45
| 58.35 | 35.766208
| 139 | 20
| 30.35
| 139.341764
| -3.386023
| 83.953
| 24.794
| 391.569
| P3
| 35 | 46
| 01.91 | 35.767197
| 139 | 20
| 34.02 | 139.342783
| -1.195503
| 222.845
| 95.543
| 391.569
| -24.147
| 390.823
| ※八高線牛浜-箱根ヶ崎間横田基地延長部回避右400Rカーブ(点検再計算)
|
| 宗像事故 | 海老津- 教育大前 P1
|
| 33 | 49
| 2.05 | 33.817236
|
| 130 | 36
| 17.14
| 130.604761
|
| 基準点
| 0
| 0
|
| 501.318
| 500
| 0.3
| P2
| 33 | 48
| 57.94 | 33.816094
| 130 | 36
| 17.42
| 130.604839
| 17.667515
| -63.428
| 3.590
| 501.318
| P3
| 33 | 48
| 54.27 | 33.815075
| 130 | 35
| 16.59
| 130.60460
| -5.322014
| -183.492
| -3.462
| 501.318
| -91.529
| -492.892
| ※鹿児島線宗像事故手前500R右カーブ
|
| 東船橋 | 津田沼 P1
|
| 35 | 41
| 58.16 | 35.699489
|
| 140 | 0
| 29.69 | 140.008247
|
| 基準点
| 0
| 0
|
| 823.268
| 800
| 2.9
| P2
| 35 | 41
| 57.18 | 35.699217
| 140 | 0
| 34.33
| 140.009536
| 0.260078
| -15.124
| 58.151
| 823.268
| P3
| 35 | 41
| 53.90 | 35.698306
| 140 | 0
| 42.38 | 140.011772
| 0.501728
| -80.866
| 217.191
| 823.268
| -809.761 | -148.517
|
| 東船橋 | 津田沼 再計算 P1
|
| 35 | 41
| 58.17 | 35.699492
|
| 140 | 0
| 29.76 | 140.008267
|
| 基準点
| 0
| 0
|
| 809.703
| 800
| 1.2
| P2
| 35 | 41
| 56.71 | 35.699086
| 140 | 0
| 35.92
| 140.009978
| 0.291855
| -22.531
| 77.201
| 809.703
| P3
| 35 | 41
| 53.03 | 35.698064
| 140 | 0
| 43.76
| 140.012156
| 0.577990
| -101.854
| 252.658
| 809.703
| -795.963 | -148.529
| ※総武線東船橋-津田沼間の垂直壁切り通し複々線右カーブ
|
| 新検見川 | -稲毛 P1
|
| 35 | 39
| 3.49 | 35.650969
|
| 140 | 04
| 47.53 | 140.079869
|
| 基準点
| 0
| 0
|
| 818.028
| 800
| 2.3
| P2
| 35 | 38
| 58.42 | 35.649561
| 140 | 04
| 59.55
| 140.083208
| 0.51907
| -78.243
| 150.734
| 818.028
| P3
| 35 | 38
| 52.41 | 35.647892
| 140 | 05
| 6.17 | 140.085047
| 1.117176
| -249.235
| 384.489
| 818.028
| -788.466 | -217.927
|
| ※総武線新検見川-稲毛間の盛り土&切り通し複々線右カーブ
| | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
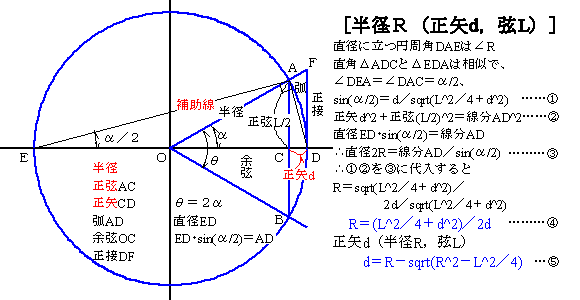
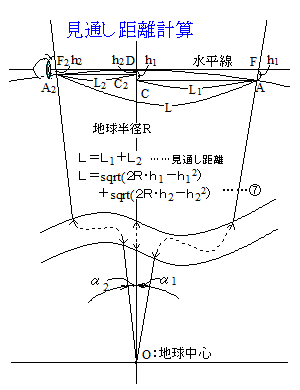 前節①式より: 2R sin(α/2)=AD
=sqrt(L2+h2)
前節①式より: 2R sin(α/2)=AD
=sqrt(L2+h2)|
mail to:
|

|
 主目次 | |||
| Last update: 2007/09/09 改7/22 (07/07/22作成) | |||||