鹿児島本線追突事故(02/02/22)について03/08/29鉄道事故調査委員会(事故調)が調査報告書を発表しました。その詳細数値から衝突状況を点検してみましょう。
推算方法としては、事故調報告書は(P71付属資料Eで)運動エネルギーから衝突速度を求めています。ここには摩擦係数0.3とか、損壊に要したエネルギーとか、不安定で確定の困難な値が使われており、衝突モデルとしては異論の余地が在り、論議・調整＝サジ加減の余地があります。
更に子細に見ますと、損壊で失われたエネルギーをゼロと仮定してこれを基準に計算しています。しかしながら反撥係数０では定量計算可能な大きな損失が出ます。実際は衝突以降一体化して移動したと思われる先行車の摩擦係数が追突車の摩擦係数(減速度)よりかなり大きいなど、いくつかの疑問点があります。（損失が無いのは反撥係数１の完全弾性衝突で、その場合で、衝突後の相対速度は逆方向で等しくなるはずです。）
一方、別の推算法としては、非常制動の減速度から衝突直後の速度を推定し、これを運動量保存則から、反撥係数0：完全非弾性衝突として質量反比例で按分すると、論議は衝突後の減速度だけになります。それは先行車のものと思われる線路上の条痕の存在から衝突前の減速度に近い値と推定されます。すなわち基準参照値ができるので妥当な理由のないサジ加減が出来なくなります。
事故調はどんな判断から前者の推算を採用し、損壊によるエネルギー損が前提の運動量保存則からは、あり得ない損壊時損失ゼロなどと、値を調整したのでしょうか？
下記計算は後者：非常減速度＋運動量保存則による事故直後の試算式です。衝突時の先行車速度Ｖf を0として使います。(↓2002/03 up)
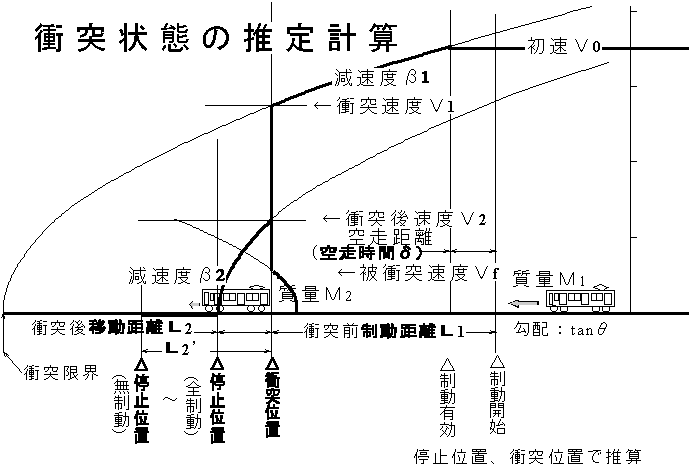【報告書記述数値】
0)．衝突時、先行車は停止していた。速度＝0
1)．衝突後移動距離推定値＝11.5ｍ 線路上の条痕より推定P20）
2)．非常制動減速度＝4.0 km/h/s (注：制動定数28.8)
3)．追突列車加速度＝1.8 km/h/s
4)．勾配tanθ＝10/1000、（惰力走行時加速度＝0.25 km/h/s：P20）
5)．先行列車７両重量＝233.6㌧(＝226.4t＋120人7.2t)P71
6)．追突列車５両重量＝172.4㌧(＝161.6t＋180人10.8t)P72
7)．推定先行列車末尾位置＝43.890 km＊印P15
（衝突後衝突面停車位置＝43.902 kmより推定）
8)．中継信号視認位置＝信号170ｍ手前＝43.630km：42号柱：中継信号喚呼票設置＊
9)．先行列車初視認位置＝末尾185ｍ手前＝43.705km＊
10).先行列車同一進路確認位置＝末尾110ｍ手前＊
11).［運転士供述］P3～事故調査報告書での採◎否×
(a)．一旦停止後無閉塞運転開始15km/hで進行
(b)．無意識に誤って警報持続ベルをリセット
(c)．中継信号進行現示を見て誤って加速
(d)．45km/hに達してノッチオフ ↓背反条件◎事故調採用
(e)．下り坂で55km/h程度に達したと思われ ↑背反条件× 〃不採用
(f)．「先行列車」を発見
(g)．同一進路上に停車！非常制動
(h)．間に合わず衝突
[以上の数値から整理すると]
12).不詳な点として、勾配加速度4).が加速度3).減速度2).に含まれているかどう
か。付属資料Ｅの数式では、勾配加速補正を行っていると思われ、含まれていない。
4')．勾配加速度4).は、惰性走行時0.25 km/h/sや加速度、減速度が走行抵抗を含んでの値は明らかなので、勾配の影響分としては、勾配正弦値を採用する。
勾配加速度＝tanθ／sqrt{１＋(tanθ)2}×ｇ×3.6
＝0.01×9.8×3.6／sqrt{１＋0.012}＝0.35278 km/h/s
13).加速点8).－衝突点距離7).＝43,890ｍ－43,890ｍ＝260ｍ。（ここを基準点に作図）
9'). 先行列車初見点43,705m－43,630m＝(260－185)＝75m（基準点より）
10').同一進路確認点＝260－110＝150m
8'). 中継信号位置170m
常用単位で表すと（km/h、km/h/s、m、秒、トン）
(5)→ Ｌs＝Ｖ0δ／3.6＋Ｖ0^2／7.2Ｂ1 ………………(5)’
(2)→ Ｖ1＝(１＋Ｍ2／Ｍ1)sqrt(7.2Ｂ2Ｌ2)＋(Ｍ2／Ｍ1)Ｖf …(2)’
(4)(2)→Ｖ0＝sqrt{(Ｂ1δ)2＋7.2Ｂ1Ｌ1＋7.2Ｂ2Ｌ2(1＋Ｍ2／Ｍ1)2}－Ｂ1δ …(4)’
勾配加速度Ａs＝35.98／sqrt{1＋(1／tanθ)2} km/h/s …………………(6)’
従って、惰性走行時間がない場合の最高速度をVm とすれば
Vm2－衝突速度Ｖ12＝7.2・減速度β1・衝突前減速距離Ｌ1 ……(7)であり
一方、加速側は、
Vm2－初速Ｖ002＝7.2・加速度α1・加速距離Ｌａ …………………(8)
Ｌａ＋衝突前減速距離Ｌ1＝加速減速距離Ｄ：260m ………………… (9)
以上３式の連立を解いてVm2、Ｌ1、Ｌａ を求めます。
(9)式から、 Ｌａ ＝Ｄ－Ｌ1 ………………………………… (10)
これを(8)式に代入すると
Vm2－Ｖ002＝7.2・α1(Ｄ－Ｌ1)＝7.2・α1・Ｄ－7.2・α1・Ｌ1
Vm2＋7.2・α1・Ｌ1＝7.2・α1・Ｄ＋Ｖ002 ……………… (8)’
(7)式を(8)’式に合わせて変形
Vm2－7.2・β1・Ｌ1＝Ｖ12 ………………………………… (7)’
(8)’－(7)’
7.2（α1＋β1）Ｌ1＝7.2・α1・Ｄ＋Ｖ002－Ｖ12
Ｌ1＝{7.2・α1・Ｄ＋Ｖ002－Ｖ12}／{7.2(α1＋β1)} …… (11)
一方(7’)式からVm2を求めると
Vm2＝7.2・β1・Ｌ1＋Ｖ12 ………Ｌ1に(11)の値を代入
Vm＝sqrt(7.2・β1・Ｌ1＋Ｖ12 ) ……………………………… (12)
実値により推定計算
勾配tanθ＝10/1000は、加速度／減速度に加算／減算され、その値は
10/1000×9.8×3.6＝0.353 km/h/s
(2)’式 衝突速度 (誤記訂正×10.5m→○11.5m)
Ｖ1＝(１＋233.6／172.4）sqrt{7.2(4－0.353)11.5}＋0 ＝40.92 km/h
(11)式 衝突前制動距離
Ｌ１＝{7.2(1.8＋0.353)260＋152－40.922}／{7.2(1.8+4.0)} ＝61.80 m
Ｌａ＝Ｄ－Ｌ1＝260－61.80＝198.20m
(12)式より、あり得る最高速度Vmは
Vm＝sqrt{7.2(4－0.353)61.80＋40.922 }＝57.42 km/h
運動エネルギーからの
試算(事故調付属資料Ｅ修正)
Last Upload:
：
Last Update＝2003/09/03
